SHORT ANSWER TYPE QUESTIONS
Q.21. Figure shows a communication system. What is the output power when input signal is of 1.01 mW ? (gain in dB = 10 log10 (Po/Pi ).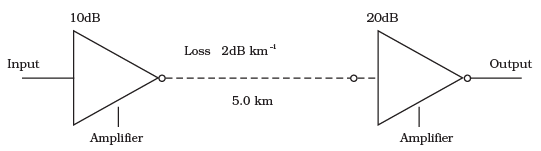 Ans.
Ans.
According to the problem, Loss suffered in path of transmission = 2 dR/km
And the distance travelled by the signal or path length is 5 km.
So, total loss suffered in 5 km = -2 x 5 = -10 dB
Total amplifier gain = 10 dB + 20 dB - 30 dB
Overall gain in signal = 30 - 10 - 20 dB
Here, it is given that gain in dB = 10 log10 (P0/Pi)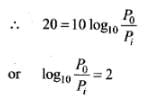
Input power is Pi =1.01 mW and P0 is the output power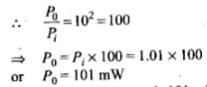
Thus, the output power is 101 mW
Q.22. A TV transmission tower antenna is at a height of 20 m. How much service area can it cover if the receiving antenna is (i) at ground level, (ii) at a height of 25 m? Calculate the percentage increase in area covered in case (ii) relative to case (i).
Ans. In this problem, height of antenna hT = 20 m
Radius of earth = 6.4 x 106 m
= 16000 m = 16 km
Area covered A = π(d)2
= 3.14 x 16 x 16 = 803.84 km2
(ii) At a height of hR = 25 m from ground level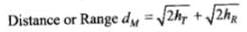
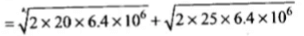
= 16 x 103 + 17.9 x 103
= 33.9 x 103 m
= 33.9 km
Area covered =π(d)2
= 3.14 x 33.9 x 33.9
= 3608.52 km2
Therefore, percentage increase in area
Q.23. If the whole earth is to be connected by LOS communication using space waves (no restriction of antenna size or tower height), what is the minimum number of antennas required? Calculate the tower height of these antennas in terms of earths radius?
Ans.
Key concept: Distance or range of transmission tower, dT =√2RhT
where, R is the radius of the earth (approximately 6400 km). hT is the height of transmission tower, .
dT is also called the radio horizon of the transmitting antenna.
Let us consider the figure given below to solve this problem.
Assume the height of transmitting antenna or receiving antenna in order to cover the entire surface of earth through communication is h1, i.e. hT = hR and radius of earth is R. If dM is the line-of-sight distance between the transmission and receiving antennas, then maximum distance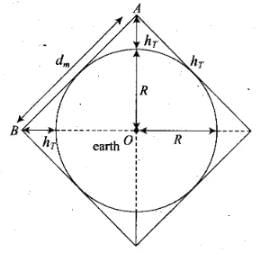 Assume the height of transmitting antenna or receiving antenna in order to cover the entire surface of earth through communication is ht i.e. hT - hR and radius of earth is R. If dM is the Line-of-sight distance between the transmission and receiving antennas,.then maximum distance
Assume the height of transmitting antenna or receiving antenna in order to cover the entire surface of earth through communication is ht i.e. hT - hR and radius of earth is R. If dM is the Line-of-sight distance between the transmission and receiving antennas,.then maximum distance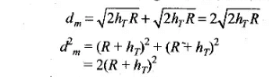
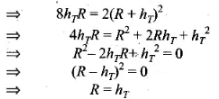
As, space wave frequency is used, so λ < <hT, hence only lower height is to be taken into consideration, In three dimensions of earth, 6 antenna towers of each of height hT = R would be used to cover entire surface of earth with communication programme.
Q.24. The maximum frequency for reflection of sky waves from a certain layer of the ionosphere is found to be fmax = 9(Nmax)1/2, where Nmax is the maximum electron density at that layer of the ionosphere.
On a certain day it is observed that signals of frequencies higher than 5MHz are not received by reflection from the F1 layer of the ionosphere while signals of frequencies higher than 8 MHz are not received by reflection from the F2 layer of the ionosphere.
Estimate the maximum electron densities of the F1 and F2 layers on that day.
Ans. According to the problem, the maximum frequency for reflection of sky waves is fmax = 9(Nmax)1/2.
where Nmax is a maximum electron density
For layer F1, fmax = 5 MHz
So, 5 x 106 = 9 (Nmax)1/2
this implies 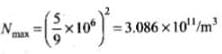
Then for layer F2, fmax = 8 MHz
So, 8 x 106 = 9 (Nmax)1/2
this implies 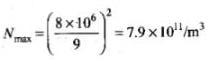
Q.25. On radiating (sending out) an AM modulated signal, the total radiated power is due to energy carried by ωc, ωc – ωm & ωc + ωm.
Suggest ways to minimise cost of radiation without compromising on information.
Ans.
Key concept: Side band frequencies. The AM wave contains three frequencies ωc, (ωc + ωm) and (ωc – ωm), ωc is called carrier frequency, (ωc + ωm) and ( ωc – ωm) are called side band frequencies.
(ωc + ωm) = Upper side band (USB) frequency
(ωc – ωm) =Lower side band (LSB) frequency
Side band frequencies are generally close to the carrier frequency.
Only side band frequencies contain information in amplitude modulated signal, [only (ωc+ ωm) and (ωc + ωm)].
Here, the total radiated power is due to energy carried by ωc, (ωc – ωm) and (ωc+ωm)
For reduction of cost of radiation without compromising on information ωc can be left and transmitting the frequencies (ωc + ωm), (ωc – ωm) or both (ωc + ωm) and (ωc – ωm).
LONG ANSWER TYPE QUESTIONS
Q.26. (i) The intensity of a light pulse travelling along a communication channel decreases exponentially with distance x according to the relation I = Ioe–αx, where Io is the intensity at x = 0 and α is the attenuation constant.
Show that the intensity reduces by 75 per cent after a distance of 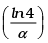
(ii) Attenuation of a signal can be expressed in decibel (dB) according to the relation dB = 10 log10 (I/I0). What is the attenuation in dB/km for an optical fibre in which the intensity falls by 50 per cent over a distance of 50 km?
Ans.
(a) According to the problem, the intensity of a light pulse travelling along a communication channel is given by I = I0e-ax
where Io is the intensity at x - 0 and α is the attenuation constant.
If the intensity is reduced by 75% that means,
I = 25% of I0
So we can write this as 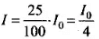
By using live above relation mentioned in the problem,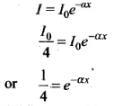
Taking natural log on both sides, we get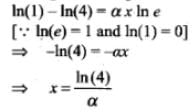
Therefore, at distance 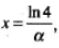 the intensity is reduced to 75% of initial intensity,
the intensity is reduced to 75% of initial intensity,
(b) Here, α is the attenuation constant expressed in dB/km. If x is the distance travelled by signal, then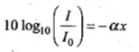 ....(1)
....(1)
where, I0 is the initial intensity.
Here 50% intensity reduced by distance 50 km So, I = 50% of I0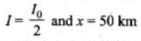
Substituting the value of x in Eq. (i),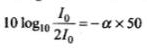
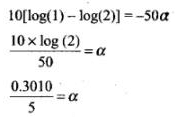
∴ The attenuation for given optical fibre α = 0.0602 dB/km
Q.27. A 50 MHz sky wave takes 4.04 ms to reach a receiver via re-transmission from a satellite 600 km above earth’s surface.
Assuming re-transmission time by satellite negligible, find the distance between source and receiver. If communication between the two was to be done by Line of Sight (LOS) method, what should size and placement of receiving and transmitting antenna be?
Ans. Let the receiver is at point A and source is at B.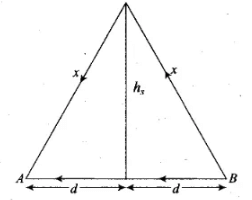 Velocity of waves= 3 x 108 m/s
Velocity of waves= 3 x 108 m/s
Time to reach a receiver = 4.04 ms = 4.04 x 10-3 s
Let the height of satellite is hs = 600 km
Radius of earth = 6400 km
Size of transmitting antenna = hT

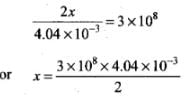
=6.06 x 105 = 606 km
Using Pythagoras theorem,
d2 = x2 - h2s = (606)2 - (600)2 = 7236
or d = 85.06 km
So, the distance between source and receiver = 2d
= 2 x 85.06= 170 km
The maximum distance covered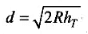
size of antenna or 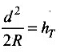

Q.28. An amplitude modulated wave is as shown in Figure Calculate
(i) the percentage modulation,
(ii) peak carrier voltage and,
(iii) peak value of information voltage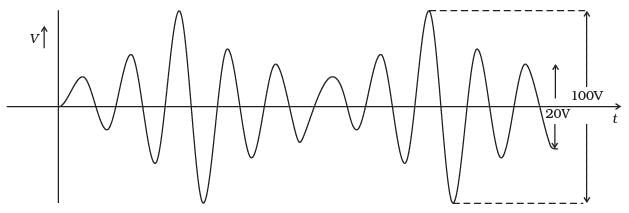
Ans.
It is observed from the above diagram that
Maximum voltage Vmax = 100/2 = 50 V
Minimum voltage Vmin = 20/2 = 10V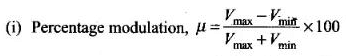
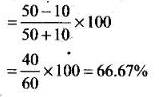

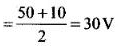
(iii) Peak value of information voltage.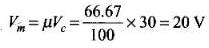
Q.29. (i) Draw the plot of amplitude versus ‘ ω’ for an amplitude modulated wave whose carrier wave (ωc) is carrying two modulating signals, ω1 and ω2 ( ω2 > ω1).
(ii) Is the plot symmetrical about ωc? Comment especially about plot in region ω < ωc.
(iii) Extrapolate and predict the problems one can expect if more waves are to be modulated.
(iv) Suggest solutions to the above problem. In the process can one understand another advantage of modulation in terms of bandwidth?
Ans.
(i) (ii) In the plotted graph shown, we note that frequency spectrum is not symmetrical about ωc. Crowding of spectrum is present for ω < ωc.
(ii) In the plotted graph shown, we note that frequency spectrum is not symmetrical about ωc. Crowding of spectrum is present for ω < ωc.
(iii) If more modulating signals are present then there will be more crowding in the modulation signal in the region ω <ωc. That will result more chances of mixing of signal.
(iv) To accommodate more signals, we should increase bandwidth and frequency carrier waves ωc. This shows that large carrier frequency enables to carry more information (i.e., more ωm) and the same will in turn increase bandwidth.
Q.30. An audio signal is modulated by a carrier wave of 20MHz such that the bandwidth required for modulation is 3kHz. Could this wave be demodulated by a diode detector which has the values of R and C as
(i) R = 1 kΩ, C = 0.01µF
(ii) R = 10 kΩ, C = 0.01µF
(iii) R = 10 kΩ, C = 0.1µF
Ans.
According to the problem, carrier wave frequency fc = 20MHz
= 20 x 106 Hz
Bandwidth required for modulation is
2fm = 3kHz = 3 x 103 Hz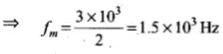
Demodulation by a diode is possible if the condition 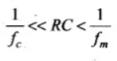 is satisfied
is satisfied
Thus 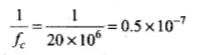 ..(i)
..(i)
and 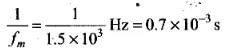 ..(ii)
..(ii)
Now, gain through all the options of R and C one by one, we get
(i) RC = 1kΩ x 0.01 μF = 103 Ω x (0.01 x 10-6F) = 10-5 s
Here, condition 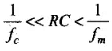 is satisfied.
is satisfied.
Hence it can be demodulated
(ii) RC = 10 kΩ x 0.01 μF = 104Ω x 10-8 F = 10-4s
Here condition 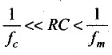 is satisfied.
is satisfied.
Hence, it can be demodulated.
(iii) RC = 10kΩ x 1 μF = 104Ω x 10-12F = 10-8s
Here, condition 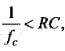 so this cannot be demodulated.
so this cannot be demodulated.



















