NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals - 2 (Exercise 3.2)
Exercise 3.2
Q1. Find x in the following figures.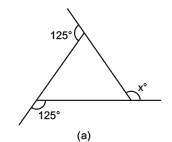
Ans:
(a)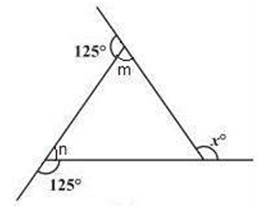
125° + m = 180° ⇒ m = 180° – 125° = 55° (Linear pair)
125° + n = 180° ⇒ n = 180° – 125° = 55° (Linear pair)
x = m + n (The exterior angle of a triangle is equal to the sum of the two opposite interior angles)
⇒ x = 55° + 55° = 110°
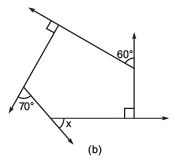
(b)
Two interior angles are right angles = 90°
70° + m = 180° ⇒ m = 180° – 70° = 110° (Linear pair)
60° + n = 180° ⇒ n = 180° – 60° = 120° (Linear pair) The figure is having five sides and is a pentagon.
Sum of interior angles of a polygon = (n-2) * 180°
Thus, sum of the angles of a pentagon = (5-2)*180° = 540°
⇒ 90° + 90° + 110° + 120° + y = 540°
⇒ 410° + y = 540° ⇒ y = 540° – 410° = 130°
x + y = 180° (Linear pair)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
Q2. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
Ans: Number of sides (n) = 9
∴ Number of exterior angles = 9
Since, sum of all the exterior angles = 360°
∵ The given polygon is a regular polygon.
∴ All the exterior angles are equal.
∴ Measure of an exterior angle = 360°/9° = 40°
(ii) 15 sides
Ans: Number sides of regular polygon = 15
∴ Number of equal exterior angles = 15 The sum of all the exterior angles = 360°
∴ The measure of each exterior angle = 360°/15 = 24°
Q3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Ans: Each exterior angle = sum of exterior angles/Number of angles
24°= 360/ Number of sides
⇒ Number of sides = 360/24 = 15
Thus, the regular polygon has 15 sides.
Q4. How many sides does a regular polygon have if each of its interior angles is 165°?
Ans: The given polygon is regular polygon.
Each interior angle = 165°
∴ Each exterior angle = 180° – 165° = 15°
∴ Number of sides = 360°/15° = 24
Thus, there are 24 sides of the polygon.
Q5. (a) Is it possible to have a regular polygon with measure of each exterior angle is 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Ans: (a) Each exterior angle = 22°
∴ Number of sides = 360°/22° = 180/11
If it is a regular polygon, then its number of sides must be a whole number.
Here, 180/11 is not a whole number.
∴ 22° cannot be an exterior angle of a regular polygon.
(b) If 22° is an interior angle, then 180° – 22°, i.e. 158° is exterior angle.
∴ Number of sides = 360°/158° = 180°/79°
Which is not a whole number.
Thus, 22° cannot be an interior angle of a regular polygon.
Q6. (a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Ans: (a) The minimum number of sides of a polygon = 3
The regular polygon of 3-sides is an equilateral.
∵ Each interior angle of an equilateral triangle = 60°
Hence, the minimum possible interior angle of a polynomial = 60°
(b) ∵ The sum of an exterior angle and its corresponding interior angle is 180°.
And minimum interior angle of a regular polygon = 60°
∴ The maximum exterior angle of a regular polygon = 180° – 60° = 120°
|
41 videos|48 docs|9 tests
|

















