NCERT Solutions for Class 10 Maths Chapter 10 - Circles (Exercise 10.1)
Exercise 10.1
Q1. How many tangents can a circle have?
Sol. A circle can have an infinite number of tangents.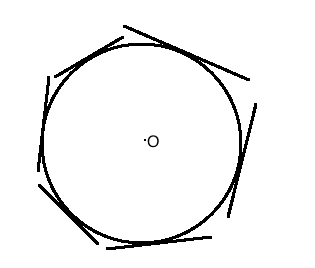
Q2. Fill in the blanks
(i) A tangent to a circle intersects it in .......... point(s).
(ii) A line intersecting a circle in two points is called a ...........
(iii) A circle can have .......... parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ...........
Sol.
(i) Exactly one
(ii) secant
(iii) two
(iv) point of contact.
Q3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length of PQ is:
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) √119 cm
Ans. (d)
Sol. 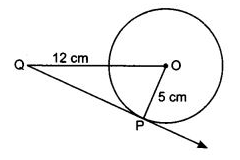
Radius of the circle = 5 cm
OQ = 12 cm
∠OPQ = 900
[The tangent to a circle is perpendicular to the radius through the point of contact]
PQ2 = OQ2 - OP2 [By Pythagoras theorem]
PQ2 = 122 - 52 = 144 - 25 = 119
PQ = √119 cm
Hence correct option is (d)
Q4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other a secant to the circle.
Sol. A line 'm' is parallel to the given line 'n' and a line 'l' which is secant is parallel to the given line 'n'.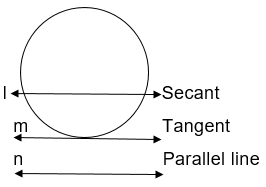
Exercise 10.2
In Q.1 to 3, choose the correct option and give justification.
Q1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Sol. From figure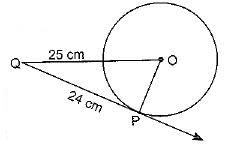
OQ2 = OP2 + PQ2
(25)2 = OP2 + (24)2
⇒ 625 - 576 = OP2
⇒ 49 = OP2
⇒ 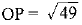
OP = 7cm
Radius of the circle = 7cm.
Hence, correct option is (a).
Q2. In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°
Sol. ∠OPT = 90°; ∠OQT = 90°; ∠POQ = 1100
TPOQ is a quadrilateral
⇒ ∠PTQ + ∠POQ = 180°
⇒ ∠PTQ + 1100 = 1800
⇒ ∠PTQ = 1800 - 1000 = 700
Hence, correct option is (b).
Q3. Choose the correct option: If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Sol. In ΔOAP and ΔOBP
OA = OB [Radii]
PA = PB
[Length of tangents from an external point are equal]
OP = OP [common]
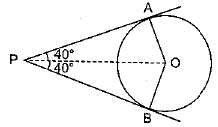
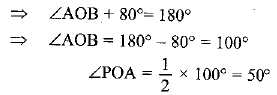
Hence, Option (a) is correct
Q4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Sol. AB is the diameter of the circle, p and q are two tangents
OA ⊥ p and OB ⊥ q and ∠1 = ∠2 = 900
⇒ p ║q [∠1 and ∠2 are alternate angles]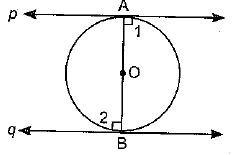
Q5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Sol. XY tangent to the circle C(O, r) at B and AB ⊥ XY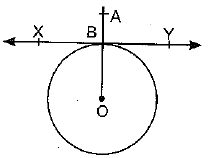
Join OB
∠ABY = 90º
∠OBY = 90º
[Radius through the point of contact is ⊥ to the tangent]
∴ ∠ABY + ∠OBY = 1800
⇒ ABO is collinear.
∴ AB passes through the centre of the circle.
Q6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Sol. OP = Radius of the circle
OA = 5 cm; AP = 4 cm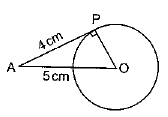
∠OPA = 90° [Radius and tangent are ⊥ar]
OA2 = AP2 + OP2 [By Pythagoras theorem]
52 = 42 + OP2
⇒ 25 = 16 + OP2
⇒ 25 - 16 = OP2
⇒ 9 = OP2
⇒ OP = √ 9 = 3
Radius = 3 cm
Q7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Sol. The radius of larger circle = 5 cm and the radius of a smaller circle = 3 cm
OP ⊥ AB [Radius of the circle is perpendicular to the tangent]
AB is a chord of the larger circle
∴ OP bisect AB AP = BP
In ΔOAP OA2 = AP2 + OP2
⇒ (5)2 = AP2 + (3)2
⇒ AP2 = 25 - 9 = 16
⇒ 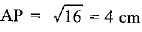
AB = 2AP = 2 x 4 = 8 cm
Q8. A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that: AB + CD = AD + BC
Sol.
AP = AS ...(i) [Lengths of tangents from an external point are equal]
BP = BQ ...(ii)
CR = CQ ...(iii)
DR = DS ...(iv)
Adding equations (i), (ii), (iii) and (iv), we get
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) +(BQ + CQ
⇒ AB + CD = AD + BC
Q9. In the figure, XY and X′ Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠AOB = 90°.
Sol. Given: Two parallel tangents to a circle with centre O. Tangent AB with point of contact C intersects XY at A and X'Y' at B
To Prove: ∠AOB = 90°
Construction: Join OA, OB and OC
Proof: In ΔAOP and ΔAOC
AP = AC [Lengths of tangents]
OP = OC [Radii]
OA = OA
⇒ ΔAOP ≅ ΔAOC [SSS congruence rule]
⇒ ∠PAO = ∠CAO [C.P.C.T]
∠PAC = 2 ∠OAC ...(i)
Similarly ∠QBC = 2 ∠OBC ...(ii)
Adding (i) and (ii), we get
∠PAC + ∠QBC = 2 [∠OAC + ∠OBC]
∠PAC + ∠QBC = 180°
[interior consecutive angle on same side of transversal]
2 = 180° [∠OAC + ∠OBC]
⇒ ∠OAC + ∠OBC = 90°
In ΔAOB, ∠AOB + [∠OAC + ∠OBC] = 180°
⇒ ∠AOB + 90° = 180°
⇒ ∠AOB = 90°
Q10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Sol. PA and PB are two tangents, and A and B are the points of contact of the tangents.
OA ⊥ AP and OB ⊥ BP
∠OAP = ∠OBP = 90°
[Radius and tangent are perpendicular to each other]
In quadrilateral OAPB
(∠OAP + ∠OBP) + ∠APB + ∠AOB = 3600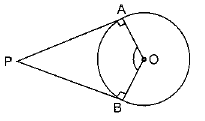
⇒ 180° + ∠APB + ∠AOB = 360°
∠APB + ∠AOB = 360° - 180° = 180°
Q11. Prove that the parallelogram circumscribing a circle is a rhombus.
Sol. Parallelogram ABCD circumscribing a circle with centre O.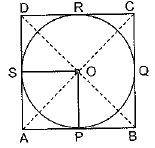
OP⊥ AB and OS ⊥ AD
In ΔOPB and ΔOSD, ∠OPB = ∠OSD [Each 90°]
OB = OD
[Diagonals of ║gm bisect each other]
OP = OS [Radii]
⇒ ΔOPB ≅ ΔOSD [RHS congruence rule]
PB = SD [C.P.C.T] ...(i)
AP = AS [Lengths of tangents]... (ii)
Adding (i) and (ii)
AP + PB = AS + DS
⇒ AB AD
Similarly AB = BC = CD = DA
∴ ║gm ABCD is a rhombus
Q12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.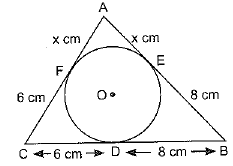
Sol. BD = 8 cm and DC = 6 cm
BE = BD = 8 cm; CD= CF = 6 cm;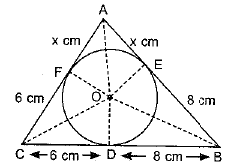
Let AE=AF = x cm
In ΔABC a = 6 + 8 = 14 cm;
b = (x + 6) cm;
c = (x +8)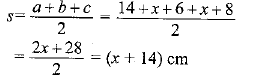
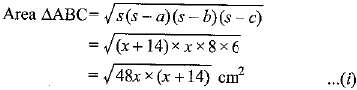
ar ΔABC = ar ΔOBC + ar ΔOCA + ar ΔOAB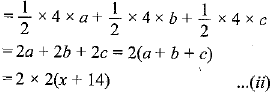
From (i) and (ii)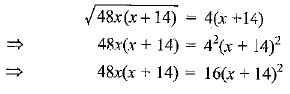
⇒ 3x(x+14) = (x + 14)2
⇒ 3x2 + 42x = x2 + 196 + 28x
⇒ 2x2 + 14x - 196 = 0
⇒ x2 + 7x - 98 = 0
⇒ x2 + 14x - 7x - 98 = 0
⇒ x(x + 14) - 7(x + 14) = 0
⇒ (x - 7)(x + 14) = 0 ⇒ x = 7
AB = x + 8 = 7 + 8 = 15 cm
AC = x + 6 = 7 + 6 = 13 cm
Q13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Sol. 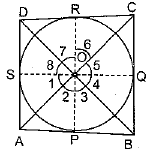
AB touches P and BC, and CD and DA touch the circle at Q, R and S.
Construction: Join OA, OB, OC, OD and OP, OO, OR, OS
∴ ∠1 = ∠2 [OA bisects ∠POS]
Similarly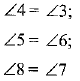
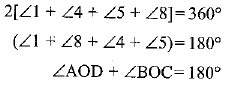
Similarly ∠AOB + ∠COD = 180°
Hence, opposite sides of quadrilateral circumscribing a circle subtend supplementary angles at the centre of a circle.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 10 - Circles (Exercise 10.1)
| 1. What is the standard equation of a circle? |  |
| 2. How can we find the radius of a circle if we know its equation? |  |
| 3. What is the relationship between the diameter and radius of a circle? |  |
| 4. How do you find the area of a circle? |  |
| 5. What are the different forms of the equation of a circle? |  |

















