NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
Q1: Find the equation of the circle with centre (0, 2) and radius 2
Ans: The equation of a circle with centre (h, k) and radius r is given as
(x – h)2 + (y – k)2 = r2
It is given that centre (h, k) = (0, 2) and radius (r) = 2.
Therefore, the equation of the circle is
(x – 0)2 + (y – 2)2 = 22
x2 + y2 + 4 – 4 +y = 4
x2 + y2 – 4y = 0
Q2: Find the equation of the circle with centre (–2, 3) and radius 4
Ans: The equation of a circle with centre (h, k) and radius r is given as
(x – h)2 + (y – k)2 = r2
It is given that centre (h, k) = (–2, 3) and radius (r) = 4.
Therefore, the equation of the circle is
(x + 2)2 + (y – 3)2 = (4)2
x2 + 4x + 4 + y2 – 6y + 9 = 16
x2 + y2+ 4x – 6y – 3 = 0
Q3: Find the equation of the circle with centre 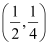 and radius
and radius 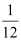
Ans: The equation of a circle with centre (h, k) and radius r is given as
(x – h)2 + (y – k)2 = r2
It is given that centre (h, k) = 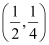 and radius (r) = .
and radius (r) = .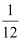
Therefore, the equation of the circle is
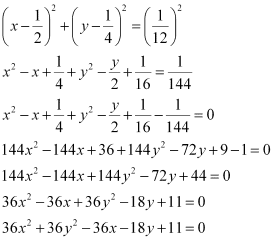
Q4: Find the equation of the circle with centre (1, 1) and radius 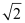
Ans: The equation of a circle with centre (h, k) and radius r is given as
(x – h)2 + (y – k)2 = r2
It is given that centre (h, k) = (1, 1) and radius (r) = 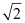 .
.
Therefore, the equation of the circle is
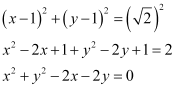
Q5: Find the equation of the circle with centre (–a, –b) and radius 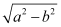
Ans: The equation of a circle with centre (h, k) and radius r is given as
(x – h)2 + (y – k)2 = r2
It is given that centre (h, k) = (–a, –b) and radius (r) = .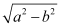
Therefore, the equation of the circle is
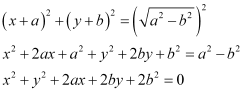
Q6: Find the centre and radius of the circle (x + 5)2 + (y – 3)2 = 36
Ans: The equation of the given circle is (x + 5)2 + (y – 3)2 = 36.
(x + 5)2 + (y – 3)2 = 36
⇒ {x – (–5)}2 + (y – 3)2 = 62, which is of the form (x – h)2 + (y – k)2 = r2, where h = –5, k = 3, and r = 6.
Thus, the centre of the given circle is (–5, 3), while its radius is 6.
Q7: Find the centre and radius of the circle x2 + y2 – 4x – 8y – 45 = 0
Ans: The equation of the given circle is x2 + y2 – 4x – 8y – 45 = 0.
x2 + y2 – 4x – 8y – 45 = 0
⇒ (x2 – 4x)+ (y2 – 8y) = 45
⇒ {x2 – 2(x)(2) + 22}+ {y2 – 2(y)(4)+ 42} – 4 –16 = 45
⇒ (x – 2)2 + (y –4)2 = 65
⇒ (x – 2)2 + (y –4)2 = , which is of the form (x – h)2 + (y – k)2 = r2, where h = 2, k = 4, and .
Thus, the centre of the given circle is (2, 4), while its radius is 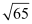 .
.
Q8: Find the centre and radius of the circle x2 + y2 – 8x+ 10y – 12 = 0
Ans: The equation of the given circle is x2 + y2 – 8x + 10y – 12 = 0.
x2 + y2 – 8x + 10y – 12 = 0
⇒ (x2 – 8x) + (y2 10y) = 12
⇒ {x2 – 2(x)(4) + 42} + {y2 2(y)(5) + 52}– 16 – 25 = 12
⇒ (x – 4)2 + (y + 5)2 = 53
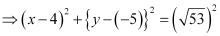 , which is of the form (x – h)2 + (y – k)2 = r2, where h = 4, k = –5, and
, which is of the form (x – h)2 + (y – k)2 = r2, where h = 4, k = –5, and 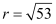 .
.
Thus, the centre of the given circle is (4, –5), while its radius is 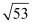 .
.
Q9: Find the centre and radius of the circle 2x2 + 2y2 – x = 0
Ans: The equation of the given circle is 2x2+ 2y2 – x = 0.
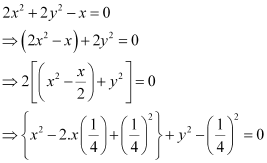
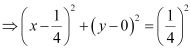
which is of the form (x – h)2 + (y – k)2 = r2, where h = 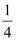 , k = 0, and
, k = 0, and 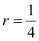 .
.
Thus, the centre of the given circle is 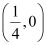 , while its radius is
, while its radius is 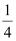 .
.
Q10: Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre is on the line 4x + y = 16.
Ans: Let the equation of the required circle be (x – h)2 + (y – k)2 = r2.
Since the circle passes through points (4, 1) and (6, 5),
(4 – h)2 + (1 – k)2 = r2 … (1)
(6 – h)2 + (5 – k)2 = r2 … (2)
Since the centre (h, k) of the circle lies on line 4x + y = 16,
4h + k = 16 … (3)
From equations (1) and (2), we obtain
(4 – h)2 + (1 – k)2 = (6 – h)2 + (5 – k)2
⇒ 16 – 8h + h2 1 – 2k + k2 = 36 – 12h + h2 + 25 – 10k + k2
⇒ 16 – 8h + 1 – 2k = 36 – 12h + 25 – 10k
⇒ 4h + 8k = 44
⇒ h + 2k = 11 … (4)
On solving equations (3) and (4), we obtain h = 3 and k = 4.
On substituting the values of h and k in equation (1), we obtain
(4 – 3)2 + (1 – 4)2 = r2
⇒ (1)2 + (– 3)2 = r2
⇒ 1+ 9 = r2
⇒ r2 = 10
⇒ 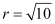
Thus, the equation of the required circle is
(x – 3)2+ (y – 4)2 = 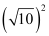
x2 – 6x + 9+ y2 – 8y + 16 = 10
x2 + y2 – 6x – 8y + 15 = 0
Q11: Find the equation of the circle passing through the points (2, 3) and (–1, 1) and whose centre is on the line x – 3y – 11 = 0.
Ans: Let the equation of the required circle be (x – h)2 + (y – k)2 = r2.
Since the circle passes through points (2, 3) and (–1, 1),
(2 – h)2 + (3 – k)2 = r2 … (1)
(–1 – h)2 + (1 – k)2 = r2 … (2)
Since the centre (h, k) of the circle lies on line x – 3y – 11 = 0,
h – 3k = 11 … (3)
From equations (1) and (2), we obtain
(2 – h)2 + (3 – k)2 = (–1 – h)2 + (1 – k)2
⇒ 4 – 4h + h2 + 9 – 6k + k2 = 1 +2h + h2 +1 – 2k + k2
⇒ 4 – 4h + 9 – 6k = 1 +2h + 1 – 2k
⇒ 6h + 4k = 11 … (4)
On solving equations (3) and (4), we obtain 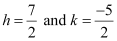 .
.
On substituting the values of h and k in equation (1), we obtain
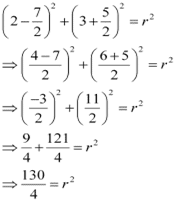
Thus, the equation of the required circle is
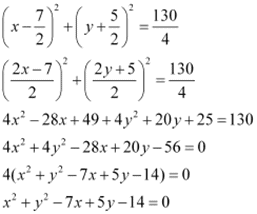
Q12: Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2, 3).
Ans: Let the equation of the required circle be (x – h)2 + (y – k)2 = r2.
Since the radius of the circle is 5 and its centre lies on the x-axis, k = 0 and r = 5.
Now, the equation of the circle becomes (x – h)2 + y2 = 25.
It is given that the circle passes through point (2, 3).
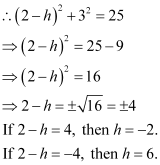
When h = –2, the equation of the circle becomes
(x + 2)2 + y2 = 25
x2 + 4x + 4 + y2 = 25
x2 + y2+ 4x – 21 = 0
When h = 6, the equation of the circle becomes
(x – 6)2 + y2 = 25
x2 – 12x + 36+ y2 = 25
x2 + y2 – 12x + 11 = 0
Q13: Find the equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes.
Ans: Let the equation of the required circle be (x – h)2 + (y – k)2 = r2.
Since the centre of the circle passes through (0, 0),
(0 – h)2 + (0 – k)2 = r2
⇒ h2 + k2 = r2
The equation of the circle now becomes (x – h)2 + (y – k)2 = h2 + k2.
It is given that the circle makes intercepts a and b on the coordinate axes. This means that the circle passes through points (a, 0) and (0, b). Therefore,
(a – h)2 + (0 – k)2 = h2 + k2 … (1)
(0 – h)2 + (b – k)2 = h2 + k2 … (2)
From equation (1), we obtain
a2 – 2ah + h2 + k2 = h2 + k2
⇒ a2 – 2ah = 0
⇒ a(a – 2h) = 0
⇒ a = 0 or (a – 2h) = 0
However, a ≠ 0; hence, (a – 2h) = 0 ⇒ h = 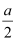 .
.
From equation (2), we obtain
h2 + b2 – 2bk + k2 = h2 + k2
⇒ b2 – 2bk = 0
⇒ b(b – 2k) = 0
⇒ b = 0 or(b – 2k) = 0
However, b ≠ 0; hence, (b – 2k) = 0 ⇒ k = 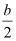 .
.
Thus, the equation of the required circle is
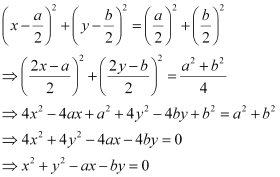
Q14: Find the equation of a circle with centre (2, 2) and passes through the point (4, 5).
Ans: The centre of the circle is given as (h, k) = (2, 2).
Since the circle passes through point (4, 5), the radius (r) of the circle is the distance between the points (2, 2) and (4, 5).
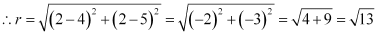
Thus, the equation of the circle is
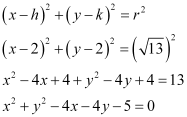
Q15: Does the point (–2.5, 3.5) lie inside, outside or on the circle x2 + y2 = 25?
Ans: The equation of the given circle is x2 + y2 = 25.
x2 + y2 = 25
⇒ (x – 0)2 + (y – 0)2 = 52, which is of the form (x – h)2 + (y – k)2 = r2, where h = 0, k = 0, and r = 5.
∴ Centre = (0, 0) and radius = 5
Distance between point (–2.5, 3.5) and centre (0, 0)
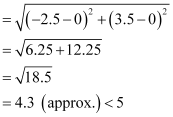
Since the distance between point (–2.5, 3.5) and centre (0, 0) of the circle is less than the radius of the circle, point (–2.5, 3.5) lies inside the circler.
|
177 videos|585 docs|160 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
| 1. What are the different types of conic sections? |  |
| 2. How are conic sections used in real life? |  |
| 3. What is the general equation of a conic section? |  |
| 4. How do you determine the type of conic section from its equation? |  |
| 5. What is the focus-directrix property of conic sections? |  |

















