NCERT Solutions Class 11 Maths Chapter 2 - Relations and Functions
Q1: Let f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.
Ans: The functions f: {1, 3, 4} → {1, 2, 5} and g: {1, 2, 5} → {1, 3} are defined as
f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}.
gof(1) = g[f(1)] = g(2) = 3 , [as f(1) = 2 and g(2) = 3]
gof(3) = g[f(3)] = g(5) = 1, [as f(3) = 5 and g(5) = 1]
gof(4) = g[f(4)] = g(1) = 3 , [as f(4) = 1 and g(1) = 3]
∴ gof = {(1, 3), (3, 1), (4, 3)}
Q2: Let f, g and h be functions from R to R. Show that
(f + g)oh = foh + goh
(f.g)oh = (foh).(goh)
Ans: To prove: (f + g)oh = foh + goh
LHS = [(f + g)oh](x)
= (f + g)[h(x)]
= f [h(x)] + g[h(x)]
= (foh)(x) + (goh)(x)
= {(foh)(x) + (goh)}(x) = RHS
∴ {(f + g)oh}(x) = {(foh)(x) + (goh)}(x) for all x ∈R
Hence, (f + g)oh = foh + goh
To Prove:
(f.g)oh = (foh).(goh)
LHS = [(f.g)oh](x)
= (f.g)[h(x)]
= f[h(x)]. g[h(x)]
= (foh)(x). (goh)(x)
= {(foh).(goh)}(x) = RHS
∴ [(f.g)oh](x) = {(foh).(goh)}(x) for all x ∈R
Hence, (f.g)oh = (foh).(goh)
Q3: Find gof and fog, if
(i) f(x) = |x| and g(x) = |5x - 2|
(ii) f(x) = 8x3 and g(x) = x1/3
Ans:
(i) f(x) = |x| and g(x) = |5x - 2|
∴ gof(x) = g(f(x)) = g(|x|) = |5|x| - 2|
fog(x) = f(g(x)) = f(|5x-2|) = ||5x - 2|| = |5x - 2|
(ii) f(x) = 8x3 and g(x) = x1/3
∴ gof(x) = g(f(x)) = g(8x3) = (8x3)1/3 = 2x
fog(x) = f(g(x)) = f(x1/3) = 8(x1/3)3 = 8x
Q4: If f(x) = (4x+3)/(6x-4), x ≠ 2/3, show that fof(x) = x, for all x ≠ 2/3. What is the inverse of f?
Ans: It is given that f(x) = (4x+3)/(6x-4), x ≠ 2/3
⇒ fo f = Ix
Hence, the given function f is invertible and the inverse of f is f itself.
Q5: State with reason whether following functions have inverse
(i) f : {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Ans: (i) f: {1, 2, 3, 4} → {10} defined as f = {(1, 10), (2, 10), (3, 10), (4, 10)}
From the given definition of f, we can see that f is a many one function as
f(1) = f(2) = f(3) = f(4) = 10
∴ f is not one – one.
Hence, function f does not have an inverse.
(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} defined as
g = {(5, 4), (6, 3), (7, 4), (8, 2)}
From the given definition of g, it is seen that g is a many one function as
g(5) = g(7) = 4.
∴ g is not one – one.
Hence, function g does not have an inverse.
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} defined as
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
It is seen that all distinct elements of the set {2, 3, 4, 5} have distinct images under h.
∴ Function h is one – one.
Also, h is onto since for every element y of the set {7, 9, 11, 13}, there exists an element x in the set {2, 3, 4, 5}, such that h(x) = y.
Thus, h is a one – one and onto function.
Hence, h has an inverse.
Q6: Show that f: [−1, 1] → R, given by f(x) = x/x + 2 is one – one. Find the inverse of the function f: [−1, 1] → Range f.
(Hint: For y ∈ Range f, y = f(x) = x/x + 2), for some x in [−1, 1], i.e.,
Ans:
f : [−1, 1] → R is given as f(x) = x/x + 2
For one – one
Let f(x) = f(y)
⇒ x/x + 2 = y/y + 2
⇒ xy + 2x = xy + 2y
⇒ 2x = 2y
⇒ x = y
∴ f is a one – one function.
It is clear that f: [−1, 1] → Range f is onto.
∴ f: [−1, 1] → Range f is one – one and onto and therefore, the inverse of the function f: [−1, 1] → Range f exists.
Let g: Range f → [−1, 1] be the inverse of f.
Let y be an arbitrary element of range f.
Since f: [−1, 1] → Range f is onto, we have
y = f(x) for some x ∈ [−1, 1]
⇒ y = xx + 2
⇒ xy + 2y = x
⇒ x(1 - y) = 2y
⇒ x = 2y/1 - y, y≠1
Now, let us define g: Range f → [−1, 1] as
g(y) = 2y/1 - y, y ≠ 1
Now,
∴ gof = x = I[-1, 1] and fog = y = IRange f
∴ f-1 = g
⇒ f-1(y) = 2y/1 - y, y ≠ 1
Q7: Consider f: R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Ans:
f: R → R is given by, f(x) = 4x + 3
For one – one
Let f(x) = f(y)
⇒ 4x + 3 = 4y + 3
⇒ 4x = 4y
⇒ x = y
∴ f is a one – one function.
For onto
For y ∈ R, let y = 4x + 3.
⇒ x = y - 3/4 ∈ R
Therefore, for any y ∈ R, there exists x = y - 34 ∈ R, such that
f(x) = f(y - 3/4) = 4(y - 3/4) + 3 = y.
∴ f is onto.
Thus, f is one – one and onto and therefore, f −1 exists.
Let us define g: R → R by g(x) = y-3/4
Now, (gof)(x) = g(f(x)) = g(4x + 3) = (4x + 3) - 3/4 = 4x/4 = x
and (fog)(y) = f(g(y)) = f(y - 3/4) = 4(y - 3/4) + 3 = y - 3 + 3 = y
∴ gof = fog = IR
Hence, f is invertible and the inverse of f is given by f - 1(y) = g(y) = y - 34.
Q8: Consider f: R+ → [4, ∞] given by f(x) = x2 + 4. Show that f is invertible with the inverse f−1 of given f by f−1(y) = √y − 4, where R+ is the set of all non-negative real numbers.
Ans: f : R+ → [4, ∞] is given as f(x) = x2 + 4.
For one – one
Let f(x) = f(y)
⇒ x2+4 = y2+4
⇒ x2 = y2
⇒ x = y [x = y, ∈ R+]
∴ f is a one – one function.
For onto For y ∈ [4, ∞), let y = x2 + 4
⇒ x2 = y − 4 ≥ 0 [as y ≥ 4]
⇒ x = √y - 4 ≥ 0
Therefore, for any y ∈ [4, ∞], there exists x = √y - 4 ∈ R+, such that f(x) = f(√y - 4) = (√y - 4)2 + 4 = y - 4 + 4 = y
∴ f is onto.
Thus, f is one – one and onto and therefore, f −1 exists.
Let us define g: [4, ∞] → R+ by g(y) = √y - 4
Now, (gof)(x) = g(f(x)) = g(x2 + 4) = √(x2 + 4) - 4 = √x2 = x
and (fog)(y) = f(g(y)) = f(√y - 4) = (√y - 4)2 + 4 = y - 4 + 4 = y
∴ gof = fog = IR
Hence, f is invertible and the inverse of f is given by f - 1(y) = g(y) = √y − 4
Q9: Consider f: R+ → [−5, ∞] given by f(x) = 9x2 + 6x − 5. Show that f is invertible with .
.
Ans: f: R+ → [−5, ∞] is given as f(x) = 9x2 + 6x − 5.
Let y be an arbitrary element of [−5, ∞).
Let y = 9x2 + 6x − 5.
⇒ y = (3x + 1)2 - 1 -5 = (3x + 1)2 - 6
⇒ (3x + 1)2 = y + 6
∴ f is onto, thereby range f = [−5, ∞).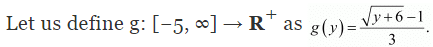
We now have:
(gof) (x) = g (f(x)) = g(9x2 + 6x - 5)
= g ((3x + 1)2 - 6)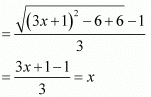
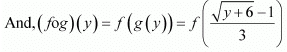
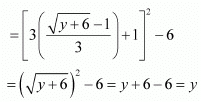
∴ gof = IR. and fo g = I[-5, ∞)
Hence, f is invertible and the inverse of f is given by
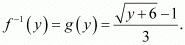
Q10: Let f: X → Y be an invertible function. Show that f has unique inverse.
(Hint: suppose g1 and g2 are two inverses of f. Then for all y ∈ Y, fog1(y) = IY(y) = fog2(y). Use one-one ness of f).
Ans: Let f: X → Y be an invertible function.
Also, suppose f has two inverses (say g1 and g2).
Then, for all y ∈ Y, we have:
fog1(y) = Iy (y) = fog2 (y)
⇒ f(g1(y)) = f(g2(y))
⇒ g1(y) = g2(y) [ f is invertible ⇒ f is one-one]
⇒ g1 = g2 [g is one-one]
Hence, f has a unique inverse.
Q11: Consider f: {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. Find f−1 and show that (f−1)−1 = f.
Ans: Function f: {1, 2, 3} → {a, b, c} is given by,
f(1) = a, f(2) = b, and f(3) = c
If we define g: {a, b, c} → {1, 2, 3} as g(a) = 1, g(b) = 2, g(c) = 3, then we have:
(fog)(a) = f (g(a)) = f(1) = a
(fog)(b) = f(g(b)) = f(2) = b
(fog)(c) = f (g(c)) = f(3) = c
And,
(gof)(1) = g(f(1)) = g(a)=l
(gof)(2) = g(f(2)) = g(b) = 2
(gof) (3) = g (f (3)) = g(c) = 3
∴ gof = Ix and fog = Iy, where X = {1, 2, 3} and Y = {a, b, c}.
Thus, the inverse of f exists and f−1 = g.
∴ f−1 : {a, b, c} → {1, 2, 3} is given by,
f−1(a) = 1, f−1(b) = 2, f-1(c) = 3
Let us now find the inverse of f−1 i.e., find the inverse of g.
If we define h: {1, 2, 3} → {a, b, c} as
h(1) = a, h(2) = b, h(3) = c, then we have:
(goh)(1) = g(h(1)) = g(a) = 1
(goh)(2) = g(h(2)) = g(b) = 2
(goh) (3) = g (h(3)) = g(c) = 3
And,
(hog)(a) = h(g(a)) = h(1) = a
(hog)(b) = h(g(b)) = h(2) = b
(hog)(c) = h (g(c)) = h(3) = c
∴ goh = Ix and hog = Iy, where X = {1, 2, 3} and Y = {a, b, c}.
Thus, the inverse of g exists and g−1 = h ⇒ (f−1)−1 = h.
It can be noted that h = f.
Hence, (f−1)−1 = f.
Q12: Let f: X → Y be an invertible function. Show that the inverse of f−1 is f, i.e., (f−1)−1 = f.
Ans: Let f: X → Y be an invertible function.
Then, there exists a function g: Y → X such that gof = IX and fog = IY.
Here, f−1 = g.
Now, gof = IX and fog = IY
⇒ f−1of = IX and fof−1 = IY
Hence, f−1: Y → X is invertible and f is the inverse of f−1
i.e., (f−1)−1 = f.
Q13: If f : R → R be given by f(x) = (3 - x3)1/3, then fof(x) is
(a) 1/x3
(b) x3
(c) x
(d) (3 − x3)
Ans: (c)
Solution: f: R → R is given as f(x) = (3 - x3)1/3.
f(x) = (3 - x3)1/3
∴ fof (x) = f (f(x)) = f((3 - x3)1/3) = [3 - ((3 - x3)1/3)3]1/3
= [3 - (3 - x3)]1/3 = (x3)1/3 = x
∴ fof (x) = x
Q14: 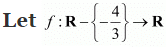
be a function defined as f(x) = 4x/(3x+4). The inverse of f is map g: Range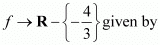
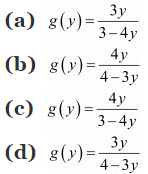
Ans: (b)
Solution:
It is given that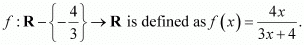
Let y be an arbitrary element of Range f.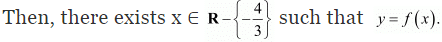
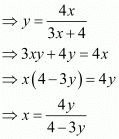
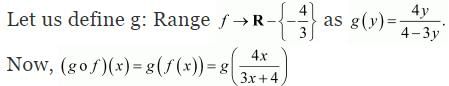
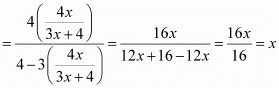
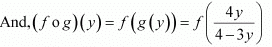
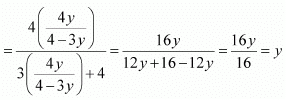
∴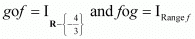
Thus, g is the inverse of f i.e., f−1 = g.
Hence, the inverse of f is the map g: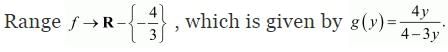
Q15: Determine whether or not each of the definition of given below gives a binary operation.
In the event that * is not a binary operation, give justification for this.
(i) On Z+, define * by a * b = a − b
(ii) On Z+, define * by a * b = ab
(iii) On R, define * by a * b = ab2
(iv) On Z+, define * by a * b = |a − b|
(v) On Z+, define * by a * b = a
Ans: (i) On Z+, * is defined by a * b = a − b.
It is not a binary operation
as the image of (1, 2) under * is 1 * 2 = 1 − 2 = −1 ∉ Z+
(ii) On Z+, * is defined by a * b = ab.
It is seen that for each a, b ∈ Z+, there is a unique element ab in Z+.
This means that * carries each pair (a, b) to a unique element a * b = ab in Z+.
Therefore, * is a binary operation.
(iii) On R, * is defined by a * b = ab2.
It is seen that for each a, b ∈ R, there is a unique element ab2 in R.
This means that * carries each pair (a, b) to a unique element a * b = ab2 in R.
Therefore, * is a binary operation. www
(iv) On Z+, * is defined by a * b = |a − b|.
It is seen that for each a, b ∈ Z+, there is a unique element |a − b| in Z+.
This means that * carries each pair (a, b) to a unique element a * b = |a − b| in Z+.
Therefore, * is a binary operation. www
(v) On Z+, * is defined by a * b = a.
It is seen that for each a, b ∈ Z+, there is a unique element a in Z+.
This means that * carries each pair (a, b) to a unique element a * b = a in Z+.
Therefore, * is a binary operation.
Q16: For each binary operation * defined below, determine whether * is commutative or associative.
(i) On Z, define a * b = a − b
(ii) On Q, define a * b = ab + 1
(iii) On Q, define a * b = ab/2
(iv) On Z+, define a * b = 2ab
(v) On Z+, define a * b = ab
(vi) On R − {−1}, define ??∗?? = a/b +1
Ans:
(i) On Z, * is defined by a * b = a − b.
It can be observed that 1 * 2 = 1 − 2 = −1 and 2 * 1 = 2 − 1 = 1.
∴ 1 * 2 ≠ 2 * 1, where 1, 2 ∈ Z
Hence, the operation * is not commutative.
Also, we have
(1 * 2) * 3 = (1 − 2) * 3 = −1 * 3 = −1 − 3 = −4
1 * (2 * 3) = 1 * (2 − 3) = 1 * −1 = 1 − (−1) = 2
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Z
Hence, the operation * is not associative.
(ii) On Q, * is defined by a * b = ab + 1.
It is known that: ab = ba for all a, b ∈ Q
⇒ ab + 1 = ba + 1 for all a, b ∈ Q
⇒ a * b = a * b for all a, b ∈ Q
Therefore, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (1 × 2 + 1) * 3 = 3 * 3 = 3 × 3 + 1 = 10
1 * (2 * 3) = 1 * (2 × 3 + 1) = 1 * 7 = 1 × 7 + 1 = 8
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Therefore, the operation * is not associative.
(iii) On Q, * is defined by a * b = ab/2
It is known that: ab = ba for all a, b ∈ Q
⇒ ab/2 = ba/2 for all a, b ∈ Q
⇒ a ∗ b = b ∗ a for all a, b ∈ Q
Therefore, the operation ∗ is commutative.
For all a, b, c ∈ Q, we have
∴ (a * b)*c = a*(b * c), where a,b,c ∈ Q
Therefore, the operation * is associative
(iv) On Z+, * is defined by a * b = 2ab.
It is known that: ab = ba for all a, b ∈ Z+
⇒ 2ab = 2ba for all a, b ∈ Z+
⇒ a * b = b * a for all a, b ∈ Z+
Therefore, the operation * is commutative.
It can be observed that
(1 ∗ 2) ∗ 3=21×2 ∗ 3 = 4 ∗ 3 = 24×3 = 212 and
1 ∗ (2 ∗ 3) = 1 ∗ 22×3 = 1 ∗ 26 = 1 ∗ 64 = 21×64 = 264
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Z+
Therefore, the operation * is not associative.
(v) On Z+, * is defined by a * b = ab.
It can be observed that
1 * 2 = 12 = 1 and 2 * 1 = 21 = 2
∴ 1 * 2 ≠ 2 * 1. where 1 .2 ∈ Z+
Therefore, the operation * is not commutative.
It can also be observed that
(2 * 3 ) * 4 = 23 * 4 = 8 * 4 = 84 = 212
and 2 * (3 * 4) = 2 * 34 = 2 * 81 = 281
∴ (2 * 3) * 4 ≠ 2 * (3 * 4), where 2, 3, 4 ∈ Z+
Therefore, the operation * is not associative.
(vi) On R, * − {−1} is defined by ??∗??= a/b + 1
It can be observed that
Therefore, the operation * is not commutative.
It can also be observed that
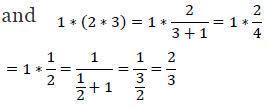
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ R − {−1} Therefore, the operation * is not associative.
Q17: Consider the binary operation ∧ on the set {1, 2, 3, 4, 5} defined by a ∧ b = min {a, b}. Write the operation table of the operation ∧.
Ans. The binary operation ∧ on the set {1, 2, 3, 4, 5} is defined as a ∧ b = min {a, b} for all a, b ∈ {1, 2, 3, 4, 5}. Thus, the operation table for the given operation ∧ can be given as:
∧ | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 2 | 2 | 2 | 2 |
3 | 1 | 2 | 3 | 3 | 3 |
4 | 1 | 2 | 3 | 4 | 4 |
5 | 1 | 2 | 3 | 4 | 5 |
Q18: Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) Is * commutative?
(iii) Compute (2 * 3) * (4 * 5).
(Hint : use the following table)
* | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 2 | 1 | 2 | 1 |
3 | 1 | 1 | 3 | 1 | 1 |
4 | 1 | 2 | 1 | 4 | 1 |
5 | 1 | 1 | 1 | 1 | 5 |
Ans: (i) (2 * 3) * 4 = 1 * 4 = 1
2 * (3 * 4) = 2 * 1 = 1
(ii) For every a, b ∈ {1, 2, 3, 4, 5}, we have a * b = b * a. Therefore, the operation*is commutative.
(iii) (2 * 3) = 1 and (4 * 5) = 1
∴ (2 * 3) * (4 * 5) = 1 * 1 = 1
Q19: Let *′ be the binary operation on the set {1, 2, 3, 4, 5} defined by a *′ b = H.C.F. of a and b. Is the operation *′ same as the operation * defined in Exercise 4 above? Justify your answer.
Ans: The binary operation *′ on the set {1, 2, 3 4, 5} is defined as a *′ b = H.C.F of a and b.
The operation table for the operation *′ can be given as:
*' | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 2 | 1 | 2 | 1 |
3 | 1 | 1 | 3 | 1 | 1 |
4 | 1 | 2 | 1 | 4 | 1 |
5 | 1 | 1 | 1 | 1 | 5 |
We observe that the operation tables for the operations * and *′ are the same.
Thus, the operation *′ is same as the operation*.
Q20: Let * be the binary operation on N given by a * b = L.C.M. of a and b. Find
(i) 5 * 7, 20 * 16
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity of * in N
(v) Which elements of N are invertible for the operation *?
Ans: The binary operation * on N is defined as a * b = L.C.M. of a and b.
(i) 5 * 7 = L.C.M. of 5 and 7 = 35
20 * 16 = L.C.M of 20 and 16 = 80
(ii) It is known that
L.C.M of a and b = L.C.M of b and a for all a, b ∈ N.
∴ a * b = b * a
Thus, the operation * is commutative.
(iii) For a, b, c ∈ N, we have
(a * b) * c = (L.C.M of a and b) * c = LCM of a, b, and c
a * (b * c) = a * (LCM of b and c) = L.C.M of a, b, and c
∴ (a * b) * c = a * (b * c)
Thus, the operation * is associative.
(iv) It is known that:
L.C.M. of a and 1 = a = L.C.M. 1 and a for all a ∈ N
⇒ a * 1 = a = 1 * a for all a ∈ N
Thus, 1 is the identity of * in N.
(v) An element a in N is invertible with respect to the operation * if there exists an element b in N, such that a * b = e = b * a.
Here, e = 1
This means that L.C.M of a and b = 1 = L.C.M of b and a
This case is possible only when a and b are equal to 1.
Thus, 1 is the only invertible element of N with respect to the operation *.
Q21: Is * defined on the set {1, 2, 3, 4, 5} by a * b = L.C.M. of a and b a binary operation? Justify your answer.
Ans: The operation * on the set A = {1, 2, 3, 4, 5} is defined as a * b = L.C.M. of a and b.
Then, the operation table for the given operation * can be given as:
* | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 2 | 3 | 4 | 5 |
2 | 2 | 2 | 6 | 4 | 10 |
3 | 3 | 6 | 3 | 12 | 15 |
4 | 4 | 4 | 12 | 4 | 20 |
5 | 5 | 10 | 15 | 20 | 5 |
It can be observed from the obtained table that
3 * 2 = 2 * 3 = 6 ∉ A,
5 * 2 = 2 * 5 = 10 ∉ A,
3 * 4 = 4 * 3 = 12 ∉ A,
3 * 5 = 5 * 3 = 15 ∉ A,
4 * 5 = 5 * 4 = 20 ∉A
Hence, the given operation * is not a binary operation.
Q22: Let * be the binary operation on N defined by a * b = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist identity for this binary operation on N?
Ans: The binary operation * on N is defined as: a * b = H.C.F. of a and b It is known that H.C.F. of a and b = H.C.F. of b and a for all a, b ∈ N.
∴ a * b = b * a
Thus, the operation * is commutative.
For a, b, c ∈ N, we have
(a * b)* c = (H.C.F. of a and b) * c = H.C.F. of a, b and c
a *(b * c) = a *(H.C.F. of b and c) = H.C.F. of a, b, and c
∴ (a * b) * c = a * (b * c)
Thus, the operation * is associative.
Now, an element e ∈ N will be the identity for the operation * if a * e = a = e* a for all a ∈ N.
But this relation is not true for any a ∈ N.
Thus, the operation * does not have any identity in N.
Q23: Let * be a binary operation on the set Q of rational numbers as follows:
(i) a * b = a − b
(ii) a * b = a2 + b2
(iii) a * b = a + ab
(iv) a * b = (a − b)2
(v) a * b= ab/4
(vi) a * b = ab2
Find which of the binary operations are commutative and which are associative.
Ans: (i) On Q, the operation * is defined as a * b = a − b. It can be observed that:
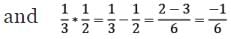
Thus, the operation * is not commutative. It can also be observed that
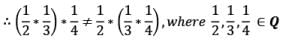
Thus the operation * is not associative.
(ii) On Q, the operation * is defined as a * b = a2 + b2.
For a, b ∈ Q. we have
a * b = a2 + b2 = b2 + a2 = b * a
∴ a * b = b * a
Thus, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (12 + 22) * 3 = (1 + 4) * 3 = 5 * 3 = 52 + 32 = 34 and
1 * ( 2 * 3 ) = 1 * (22 + 32 ) = 1 * (4 + 9) = 1 * 13 = 12 + 132 =170
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Thus, the operation * is not associative.
(iii) On Q, the operation * is defined as a * b = a + ab.
It can be observed that
1 * 2 = 1 + 1 × 2 = 1 + 2 = 3
2 * 1 = 2 + 2 × 1 = 2 + 2 = 4
∴ 1 * 2 ≠ 2 * 1, where 1, 2 ∈ Q
Thus, the operation * is not commutative.
It can also be observed that
(1 * 2) * 3 = (1 + 1 × 2) * 3 = (1 + 2) * 3 = 3 * 3 = 3 + 3 × 3 = 3 + 9 = 12 and
1 * (2 * 3) = 1 * (2 + 2 × 3) = 1 * (2 + 6) = 1 * 8 = 1 + 1 × 8 =1 + 8 = 9
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Thus, the operation * is not associative.
(iv) On Q, the operation * is defined by a * b = (a − b)2.
For a, b ∈ Q, we have
a * b = (a - b)2
b * a = (b - a)2 = [- (a - b)] 2 = (a - b)2
∴ a* b = b* a
Thus, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (1 - 2)2 * 3 = ( - 1) 2 * 3 = 1 * 3 = (1 - 3)2 = (- 2)2
and 1 * (2 * 3) = 1 * (2 - 3)2 = 1 * (- 1)2 = 1 * 1 = (1 - 1)2 = 0
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Thus, the operation * is not associative.
(v) On Q, the operation * is defined as a * b = ab/4
For a, b ∈ Q, we have
a * b = ab/4 = ba/4 = b * a
∴ a * b = b * a
Thus, the operation * is commutative.
For a, b, c ∈ Q, we have
∴ (a * b) * c = a * (b * c), where a, b, c ∈ Q
Thus, the operation * is associative.
(vi) On Q, the operation * is defined as a * b = ab2
It can be observed that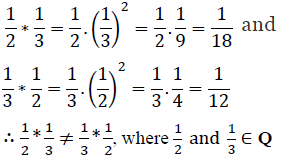
Thus, the operation * is not commutative.
It can also be observed that
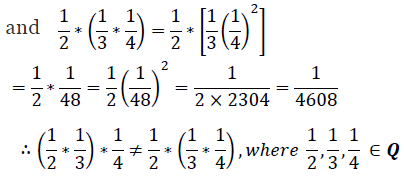
Thus, the operation * is not associative.
Hence, the operations defined in (ii), (iv), (v) are commutative and the operation defined in (v) is associative.
Q24: Find which of the operations given above has identity.
Ans: An element e ∈ Q will be the identity element for the operation *
if a * e = a = e * a, for all a ∈ Q.
However, there is no such element e ∈ Q with respect to each of the six operations satisfying the above condition.
Thus, none of the six operations has identity.
Q25: Let A = N × N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d) Show that * is commutative and associative. Find the identity element for * on A, if any.
Ans: A = N × N and * is a binary operation on A and is defined by (a, b) * (c, d) = (a + c, b + d)
Let (a, b), (c, d) ∈ A
Then, a, b, c, d ∈ N
We have:
(a, b) * (c, d) = (a + c, b + d)
(c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)
[Addition is commutative in the set of natural numbers]
∴ (a, b) * (c, d) = (c, d) * (a, b)
Therefore, the operation * is commutative.
Now, let (a, b), (c, d), (e, f) ∈ A
Then, a, b, c, d, e, f ∈ N
We have
[(a, b) ∗ (c, d)] ∗ (e, f) = (a + c, b + d) ∗ (e, f) = (a + c + e, b + d + f)
and (a, b) ∗ (c, d)] ∗ (e, f) ] = (a + c + e, b + d + f)
∴ [(a, b) ∗ (c, d)] ∗ (e, f) = (a, b) ∗ [(c, d) ∗ (e, f)]
Therefore, the operation * is associative.
Let an element e=(e1, e2)∈ A will be an identity element for the operation *
if a * e = a = e * a for all a=(a1, a2)∈ A
i.e.,(a1 + e1, a2 + e2) = (a1, a2) = (e1 + a1, e2 + a2)
Which is not true for any element in A.
Therefore, the operation * does not have any identity element.
Q26: State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N, a * a = a ∀ a ∈ N.
(ii) If * is a commutative binary operation on N, then a * (b * c) = (c * b) * a
Ans:
(i) Define an operation * on N as a * b = a + b ∀ a, b ∈ N
Then, in particular, for b = a = 3, we have
3 * 3 = 3 + 3 = 6 ≠ 3
Therefore, statement (i) is false.
(ii) R.H.S. = (c * b) * a
= (b * c) * a [* is commutative]
= a * (b * c) [Again, as * is commutative]
= L.H.S.
∴ a * (b * c) = (c * b) * a
Therefore, statement (ii) is true.
Q27: Consider a binary operation * on N defined as a * b = a3 + b3. Choose the correct answer.
(a) Is * both associative and commutative?
(b) Is * commutative but not associative?
(c) Is * associative but not commutative?
(d) Is * neither commutative nor associative?
Ans: (b)
Solution: On N, the operation * is defined as a * b = a3 + b3.
For, a, b, ∈ N, we have
a * b = a3 + b3 = b3 + a3 = b * a [Addition is commutative in N]
Therefore, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (13 + 23) * 3 = (1 + 8) * 3 = 9 * 3 = 93 + 33 = 729 + 27 = 756
and 1* (2 * 3) = 1 * (23 + 33) = 1* (8 + 27) = 1 * 35 = 13 + 353 = 1 + 42875 = 42876
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ N
Therefore, the operation * is not associative.
Hence, the operation * is commutative, but not associative.
|
203 videos|307 docs|139 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 2 - Relations and Functions
| 1. What is the difference between a relation and a function? |  |
| 2. How can you determine if a relation is a function? |  |
| 3. What is the domain of a function? |  |
| 4. How do you find the range of a function? |  |
| 5. What is the importance of relations and functions in mathematics? |  |






















