NCERT Solutions Class 11 Maths Chapter 3 - Trigonometric Functions
Q1: 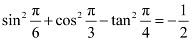
Ans: L.H.S. = 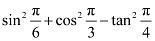
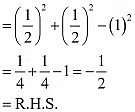
Q2: Prove that 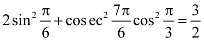
Ans: L.H.S. = 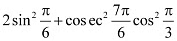
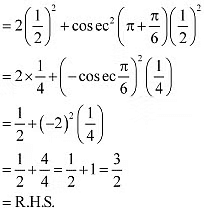
Q3: Prove that 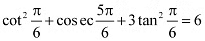
Ans: L.H.S. = 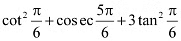
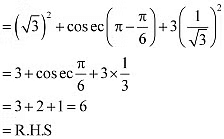
Q4: Prove that 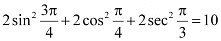
Ans: L.H.S = 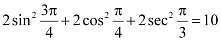
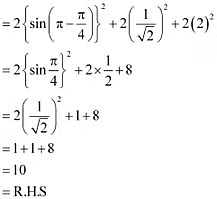
Q5: Find the value of:
(i) sin 75°
(ii) tan 15°
Ans: (i) sin 75° = sin (45°+ 30°)
= sin 45° cos 30° + cos 45° sin 30°
[sin (x + y) = sin x cos y + cos x sin y]
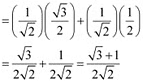
(ii) tan 15° = tan (45° – 30°)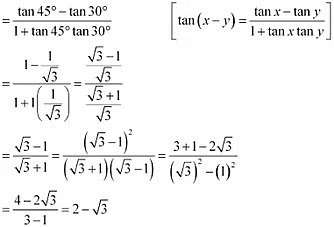
Q6: Prove that: 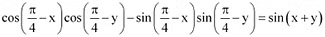
Ans: 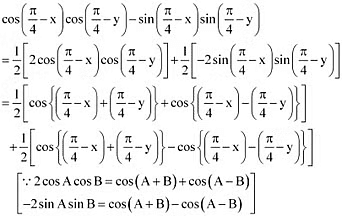
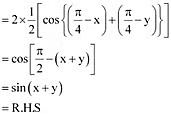
Q7: Prove that: 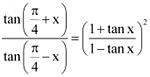
Ans: It is known that 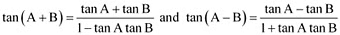
∴ L.H.S. = 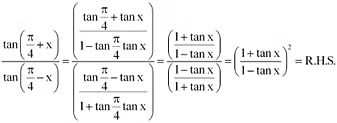
Q8: Prove that 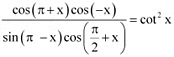
Ans: 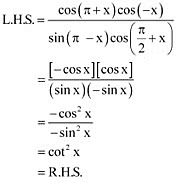
Q9: 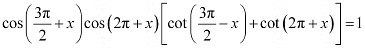
Ans: L.H.S. = 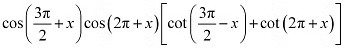
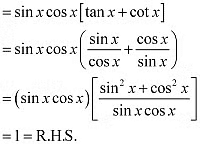
Q10: Prove that sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x
Ans: L.H.S. = sin (n + 1)x sin(n + 2)x + cos (n + 1)x cos(n + 2)x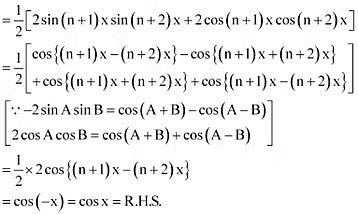
Q11: Prove that 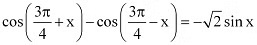
Ans: It is known that 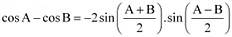 .
.
∴L.H.S. = 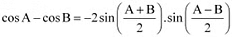
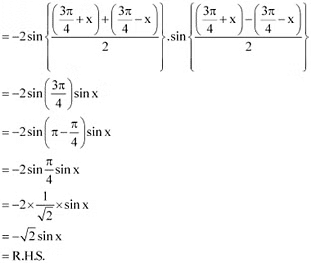
Q12: Prove that sin2 6x – sin2 4x = sin 2x sin 10x
Ans: It is known that
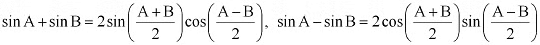
∴ L.H.S. = sin26x – sin24x
= (sin 6x + sin 4x) (sin 6x – sin 4x) 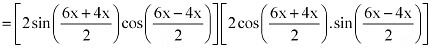
= (2 sin 5x cos x) (2 cos 5x sin x)
= (2 sin 5x cos 5x) (2 sin x cos x)
= sin 10x sin 2x
= R.H.S.
Q13: Prove that cos2 2x – cos2 6x = sin 4x sin 8x
Ans: It is known that
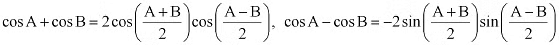
∴ L.H.S. = cos2 2x – cos2 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
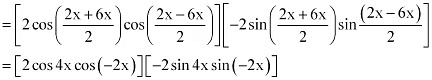
= [2 cos 4x cos 2x] [–2 sin 4x (–sin 2x)]
= (2 sin 4x cos 4x) (2 sin 2x cos 2x)
= sin 8x sin 4x
= R.H.S.
Q14: Prove that sin 2x + 2sin 4x + sin 6x = 4cos2 x sin 4x
Ans: L.H.S. = sin 2x + 2 sin 4x + sin 6x
= [sin 2x + sin 6x] +2 sin 4x
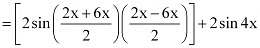
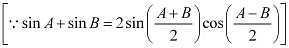
= 2 sin 4x cos (– 2x)+ 2 sin 4x
= 2 sin 4x cos 2x + 2 sin 4x
= 2 sin 4x (cos 2x + 1)
= 2 sin 4x (2 cos2 x – 1+ 1)
= 2 sin 4x (2 cos2 x)
= 4cos2 x sin 4x
= R.H.S.
Q15: Prove that cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Ans: L.H.S = cot 4x (sin 5x sin 3x)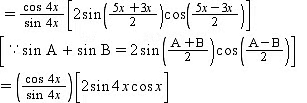
= 2 cos 4x cos x
R.H.S. = cot x (sin 5x – sin 3x)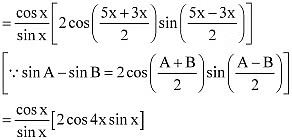
= 2 cos 4x. cos x
L.H.S. = R.H.S.
Q16: Prove that 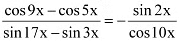
Ans: It is known that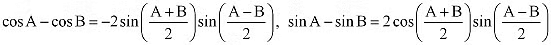
∴ L.H.S = 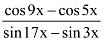
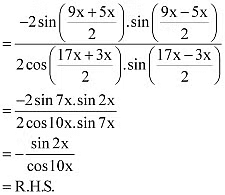
Q17: Prove that 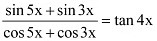
Ans: It is known that
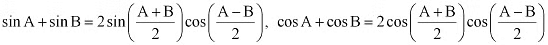
∴L.H.S. = 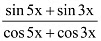
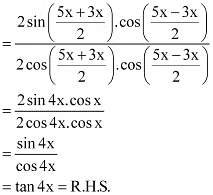
Q18: Prove that 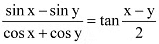
Ans: It is known that
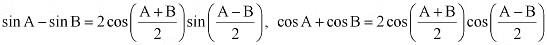
∴ L.H.S. = 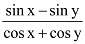
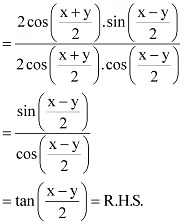
Q19: Prove that 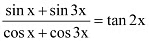
Ans: It is known that
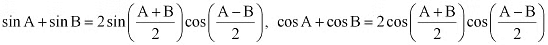
∴L.H.S. = 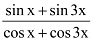
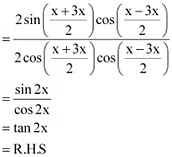
Q20: Prove that 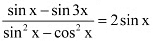
Ans: It is known that
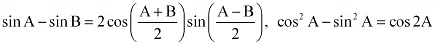
∴L.H.S. = 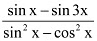
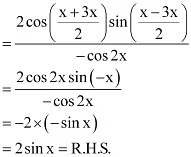
Q21: Prove that 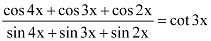
Ans: L.H.S. = 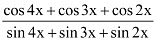
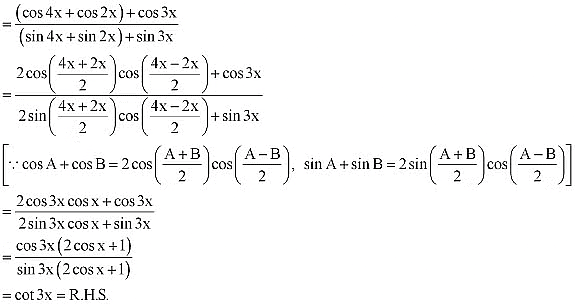
Q22: Prove that cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
Ans: L.H.S. = cot x cot 2x – cot 2x cot 3x – cot 3x cot x
= cot x cot 2x – cot 3x (cot 2x + cot x)
= cot x cot 2x – cot (2x + x) (cot 2x + cot x)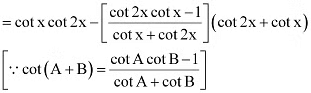
= cot x cot 2x – (cot 2x cot x – 1)
= 1 = R.H.S.
Q23: Prove that 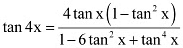
Ans: It is known that 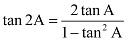 .
.
∴ L.H.S. = tan 4x = tan 2(2x)
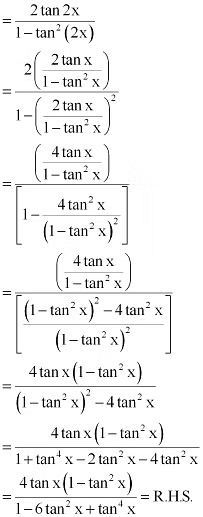
Q24: Prove that cos 4x = 1 – 8sin2 x cos2 x
Ans: L.H.S. = cos 4x
= cos 2(2x)
= 1 – 2 sin2 2x [cos 2A = 1 – 2 sin2 A]
= 1 – 2(2 sin x cos x)2 [sin2A = 2sin A cosA]
= 1 – 8 sin2x cos2x
= R.H.S.
Q25: Prove that: cos 6x = 32 cos6 x – 48 cos4 x + 18 cos2 x – 1
Ans: L.H.S. = cos 6x
= cos 3(2x)
= 4 cos3 2x – 3 cos 2x [cos 3A = 4 cos3 A – 3 cos A]
= 4 [(2 cos2 x – 1)3 – 3 (2 cos2 x – 1) [cos 2x = 2 cos2 x – 1]
= 4 [(2 cos2 x)3 – (1)3 – 3 (2 cos2 x)2 + 3 (2 cos2 x)] – 6cos2 x + 3
= 4 [8cos6x – 1 – 12 cos4x + 6 cos2x] – 6 cos2x + 3
= 32 cos6x – 4 – 48 cos4x + 24 cos2 x – 6 cos2x + 3
= 32 cos6x – 48 cos4x + 18 cos2x – 1
= R.H.S.
|
172 videos|503 docs|154 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 3 - Trigonometric Functions
| 1. What are the basic trigonometric functions? |  |
| 2. How are trigonometric functions used in real-life applications? |  |
| 3. What is the unit circle and how is it related to trigonometric functions? |  |
| 4. How do you find the values of trigonometric functions for angles beyond 90 degrees? |  |
| 5. Can trigonometric functions be used to solve for unknown sides and angles in a triangle? |  |
















