NCERT Solutions for Class 7 Maths Chapter 6 Number Play
| Table of contents |

|
| Page No. 127 |

|
| Page No. 128 |

|
| Page No. 129 |

|
| Page No. 130 |

|
| Page No. 131 |

|
| Page No. 132 |

|
| Page No. 133 |

|
| Page No. 134 |

|
| Page No. 136 |

|
| Page No. 137 |

|
| Page No. 141 |

|
| Page No. 142 |

|
| Page No. 143 |

|
Page No. 127
Q1: What do the numbers in the figure below tell us?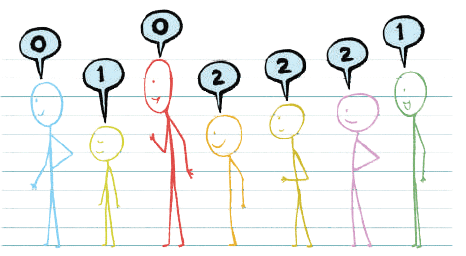 Ans: In the figure, the children have numbers above their heads: 0, 1, 0, 2, 2, 2, 1.
Ans: In the figure, the children have numbers above their heads: 0, 1, 0, 2, 2, 2, 1.
These numbers show how many taller people are there in front of that particular person.
Q2: What do you think these numbers mean?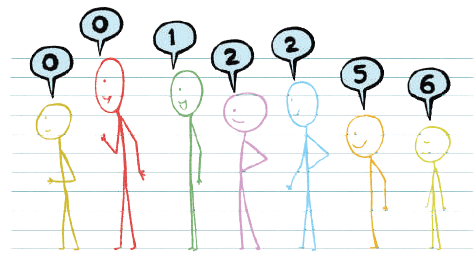 Ans: In the figure, each number shows how many taller people are standing in front of a person.
Ans: In the figure, each number shows how many taller people are standing in front of a person.
For example, the number above the second person is 0, which means no one taller is standing in front of him.
Page No. 128
Q1: Write down the number each child should say based on this rule for the arrangement shown below.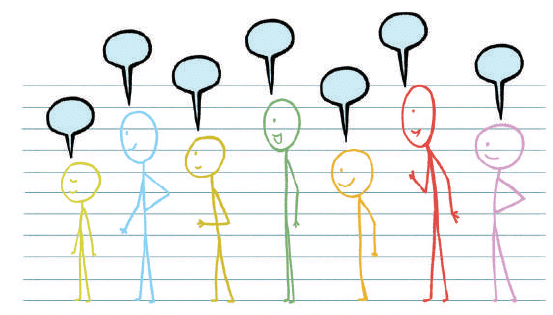 Ans: Do it Yourself!
Ans: Do it Yourself!
Figure it Out
Q1: Arrange the stick figure cutouts given at the end of the book or draw a height arrangement such that the sequence reads: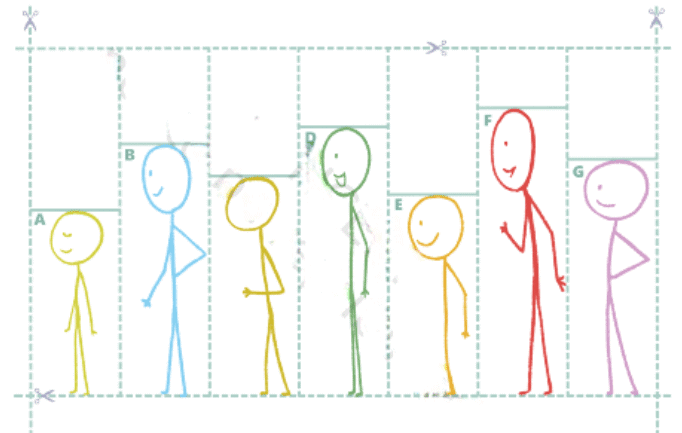 (a) 0, 1, 1, 2, 4, 1, 5
(a) 0, 1, 1, 2, 4, 1, 5
Ans: The required arrangement is FCBGADE.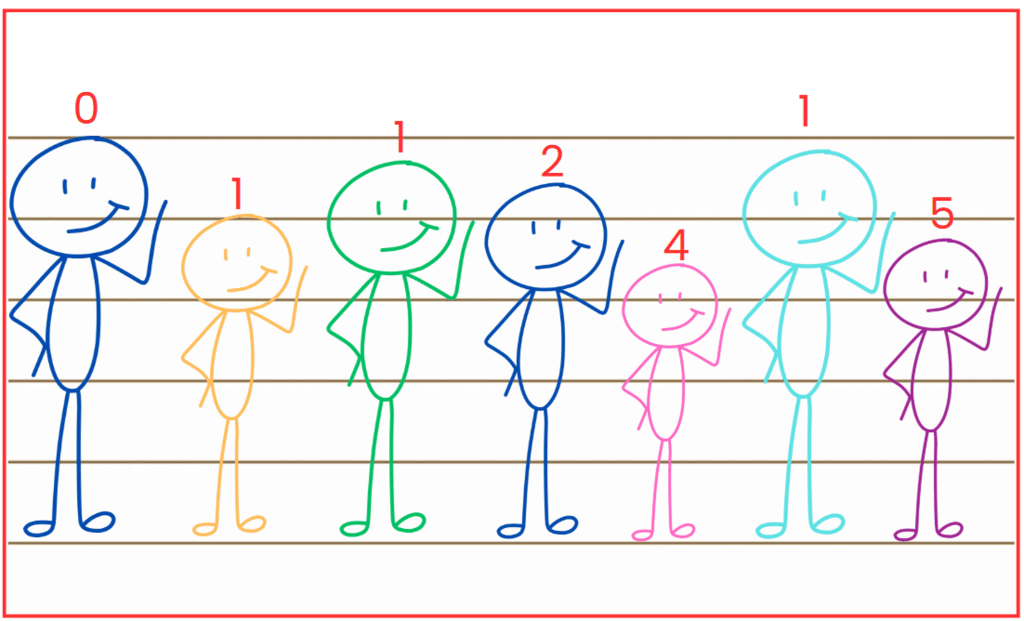
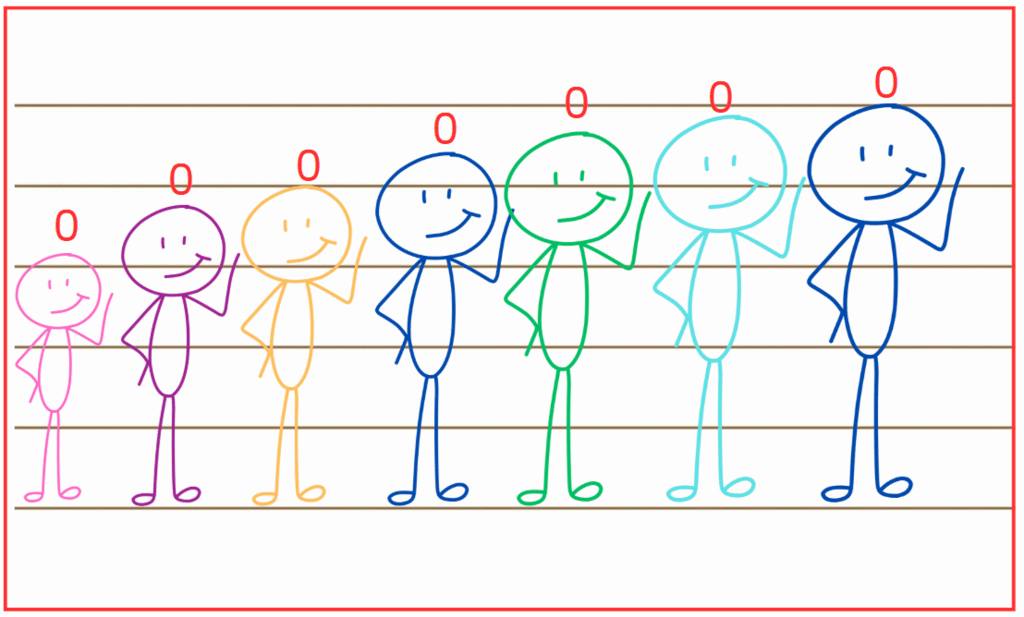
(b) 0, 0, 0, 0, 0, 0, 0
Ans: The required arrangement is AECGBDF.
(c) 0, 1, 2, 3, 4, 5, 6
Ans: The required arrangement is FDBGCEA.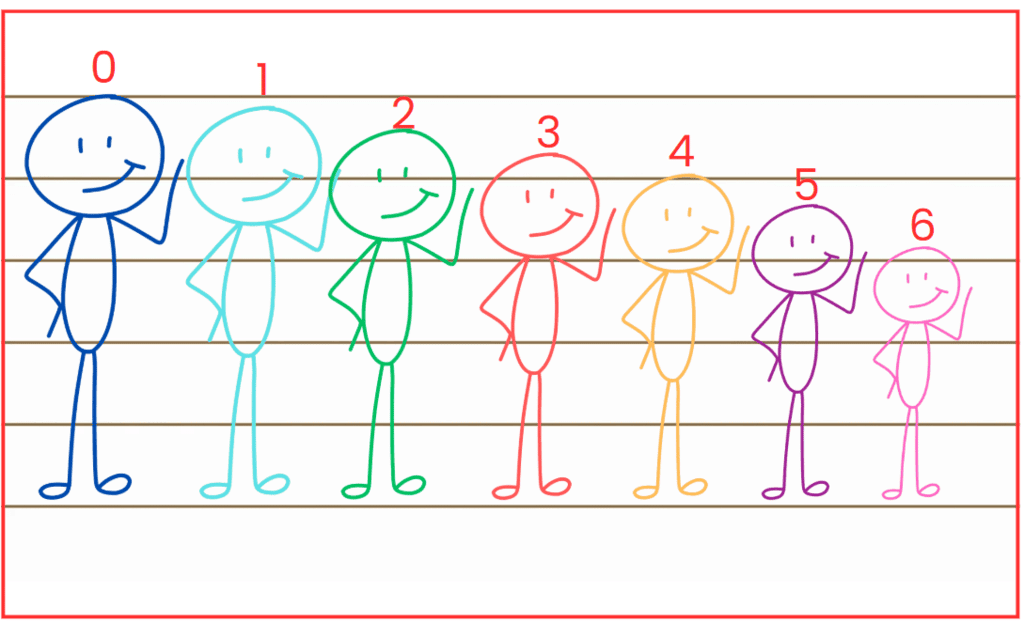
(d) 0, 1, 0, 1, 0, 1, 0
Ans: The required arrangement is EAGCDBF.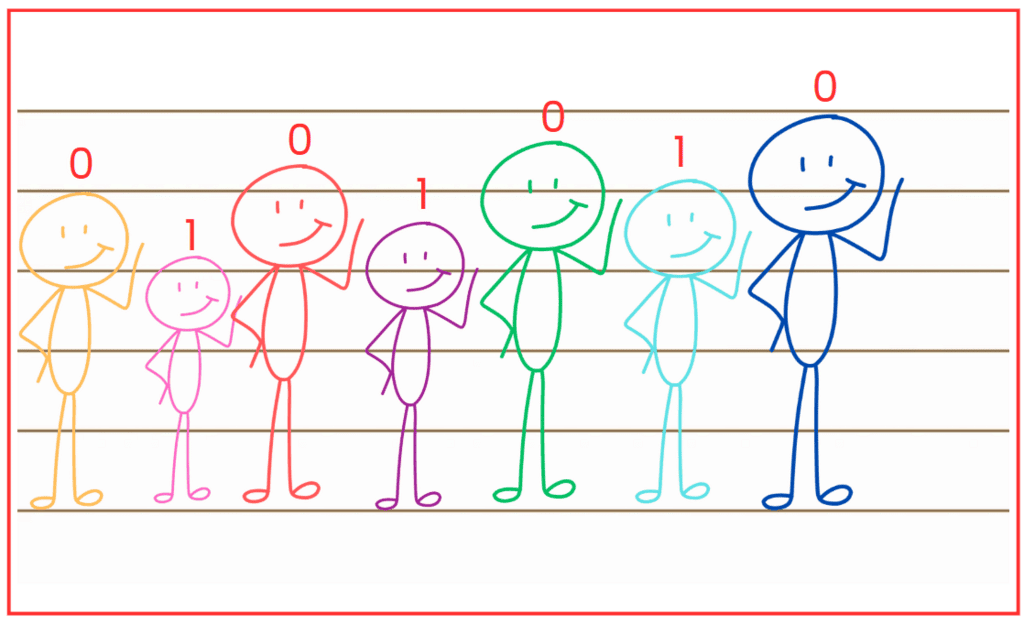
(e) 0, 1, 1, 1, 1, 1, 1
Ans: The required arrangement is FAECGBD.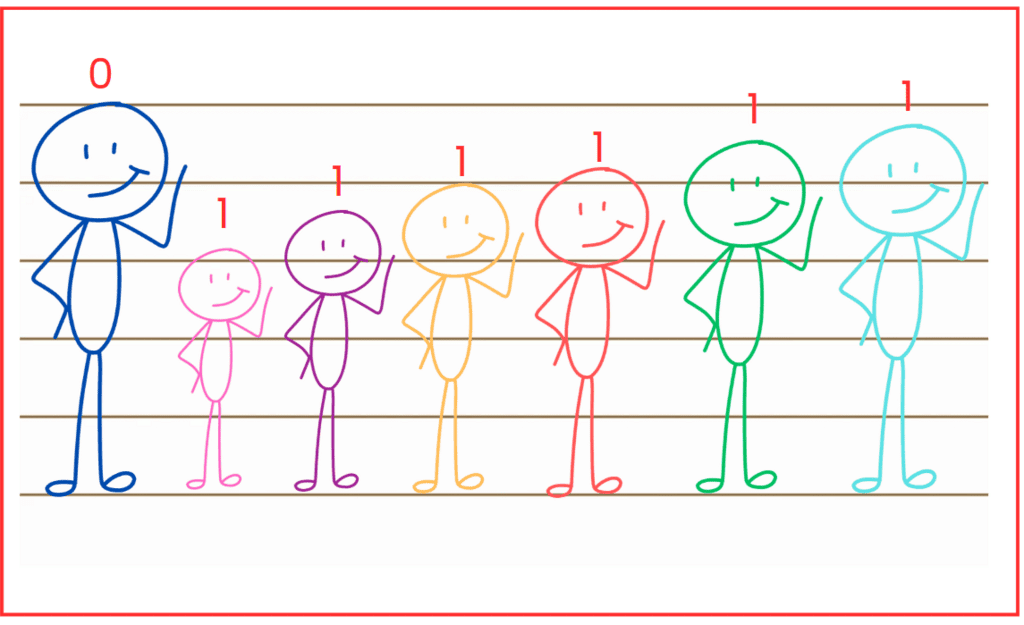
(f) 0, 0, 0, 3, 3, 3, 3
Ans: The required arrangement is BDFAECG.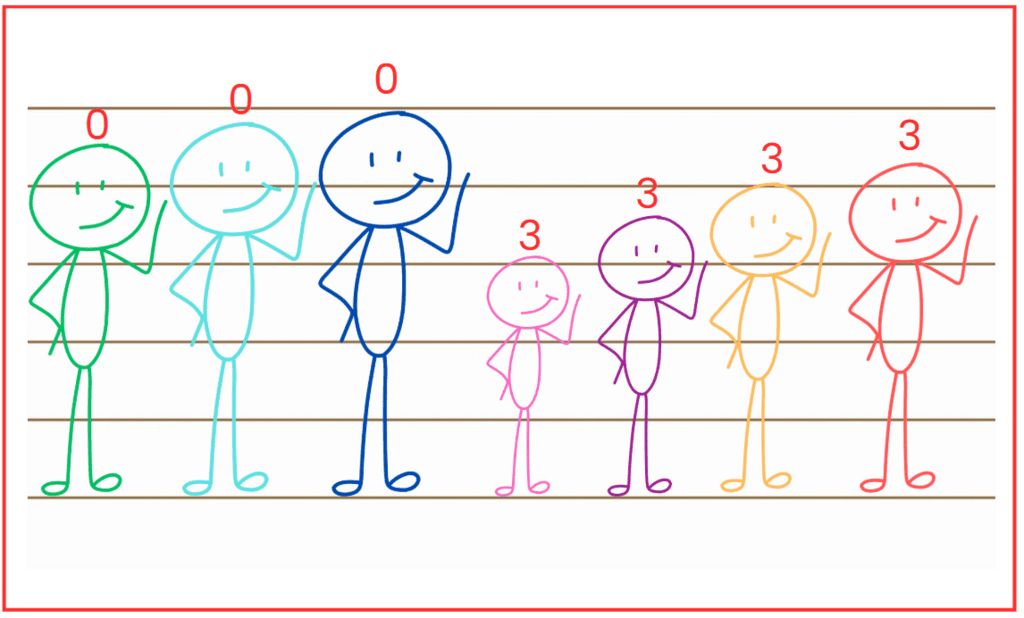
Q2: For each of the statements given below, think and identify if it is Always True, Only Sometimes True, or Never True. Share your reasoning.
(a) If a person says '0', then they are the tallest in the group.
Ans: Only Sometimes True: A person says ‘0’ when they see no one taller than themselves. The tallest person will always say ‘0’, but a shorter person can also say ‘0’ if they are at the front or in a position where no one taller is ahead of them. Thus, the given statement is only sometimes true.
(b) If a person is the tallest, then their number is '0'.
Ans: Always True: If a person is the tallest, then no one is taller than them, so they will always say ‘0’. So, the given statement is always true.
(c) The first person's number is '0'.
Ans: Always True: Each person is assigned a number that represents how many taller people are ahead of them. Since there is no one ahead of the first person, their number will always be ‘0’. Hence, the given statement is always true.
(d) If a person is not first or last in line (i.e., if they are standing somewhere in between), then they cannot say '0'.
Ans: Only Sometimes True. A person in between can say 0 if no one ahead is taller (e.g., second tallest in second position).
(e) The person who calls out the largest number is the shortest.
Ans: Only Sometimes True: The statement is only sometimes true. A person who calls out the largest number has many taller people in front but may not be the shortest overall. For example, if the shortest person is standing at the front, they will call out ‘0’. Meanwhile, the second shortest person could be at the back and might call out the largest number.
(f) What is the largest number possible in a group of 8 people?
Ans: If there are 8 people, then the shortest person will see 7 taller people. So the maximum number someone can say is 7.
Page No. 129
Q1: Kishor has some number cards and is working on a puzzle: There are 5 boxes, and each box should contain exactly 1 number card. The numbers in the boxes should sum to 30. Can you help him find a way to do it?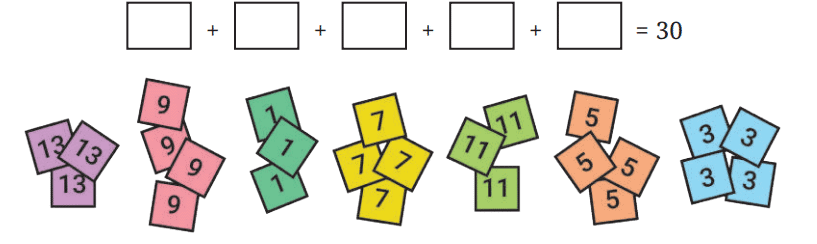
Can you figure out which 5 cards add to 30? Is it possible? Are there many ways of choosing 5 cards from this collection? Is there a way to find a solution without checking all possibilities?
Ans: No, it is not possible, as the sum of 5 odd numbers is always odd, but 30 is an even number.
Q2: Add a few even numbers together. What kind of number do you get? Does it matter how many numbers are added?
 Ans: When even numbers are added together, the sum will always be an even number, regardless of how many numbers are added.
Ans: When even numbers are added together, the sum will always be an even number, regardless of how many numbers are added.
For example, adding 2 + 4 gives 6, an even number. Similarly, adding 8 + 2 + 4 results in 14, which is still an even number.
Thus, the sum of any even numbers will always be even, no matter how many numbers are added.
Q3: Now, add a few odd numbers together. What kind of number do you get? Does it matter how many odd numbers are added? Ans: When odd numbers are added together, the sum will always be odd if an odd number of odd numbers are added. If an even number of odd numbers are added, the sum will be even.
Ans: When odd numbers are added together, the sum will always be odd if an odd number of odd numbers are added. If an even number of odd numbers are added, the sum will be even.
For example:
- 3 + 5 = 8 (even)
- 3 + 5 + 7 = 15 (odd)
So, adding odd numbers together gives an odd or even result based on the number of odd numbers being added.
Page No. 130
Q1: What about adding 3 odd numbers? Can the resulting sum be arranged in pairs? No.
Ans: The sum of 3 odd numbers is odd and cannot be arranged in pairs (e.g., 1 + 3 + 5 = 9).
Q2: Explore what happens to the sum of (a) 4 odd numbers, (b) 5 odd numbers, and (c) 6 odd numbers.
Ans: Based on the given examples for number cards 1, 3, 5, 7, 9, 11, 13.
(a) Sum of 4 odd numbers = 1 + 3 + 5 + 7 = 16 (even), can be arranged in pairs.
(b) Sum of 5 odd numbers = 1 + 3 + 5 + 7 + 9 = 25 (odd), cannot be arranged in pairs.
(c) Sum of 6 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 = 36 (even), can be arranged in pairs.
Page No. 131
Figure it Out
Q1: Using your understanding of the pictorial representation of odd and even numbers, find out the parity of the following sums:
(a) Sum of 2 even numbers and 2 odd numbers (e.g., even + even + odd + odd)
Ans:
- Even + Even = Even and Odd + Odd = Even.
- Adding the two results, we get Even + Even = Even.
- The parity of the result is even.
- Example: 2 + 4 + 3 + 5 = 6 + 8 = 14 (Even)
(b) Sum of 2 odd numbers and 3 even numbers
Ans:
- Two odd numbers: Their sum is even (e.g., 3 + 5 = 8, even), as the extra ones pair up.
- Three even numbers: Each is even, so their sum is even (e.g., 2 + 4 + 6 = 12, even).
- Sum: (even) + (even) = even.
The sum of 2 odd numbers and 3 even numbers is even.
(c) Sum of 5 even numbers
Ans:
- Each even number is a complete pair. Adding any number of even numbers keeps the sum as pairs.
- Example: 2 + 4 + 6 + 8 + 10 = 30, even.
The sum of 5 even numbers is even.
(d) Sum of 8 odd numbers
Ans:
- Odd + Odd = Even (4 such pairs).
- Adding the 4 such results, we get
- Even + Even + Even + Even = Even
- The parity of the result is even.
- Example: 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64 (Even)
Q2: Lakpa has an odd number of ₹1 coins, an odd number of ₹5 coins, and an even number of ₹10 coins in his piggy bank. He calculated the total and got ₹205. Did he make a mistake? If he did, explain why. If he didn’t, how many coins of each type could he have?
Ans:
The total value of an odd number of ₹1 coins is odd.
The total value of an odd number of ₹5 coins is odd.
The total value of an even number of ₹10 coins is even.
Adding the values of all the coins:
Odd + Odd + Even = Even + Even = Even.
Therefore, the parity of the sum of ₹1 coins, ₹5 coins, and ₹10 coins is even.
But Lakpa calculated a total of ₹205, which is odd.
Therefore, Lakpa must have made a mistake!
The total can never be ₹205 with the given coin counts.
Q3: We know that:
(a) even + even = even
(b) odd + odd = even
(c) even + odd = odd
Similarly, find out the parity for the scenarios below:
(d) even - even =
Ans: Example:
6 – 2 = 4 → even
8 – 4 = 4 → even
Parity of result = even
∴ even – even = even
(e) odd - odd =
Ans: Example:
7 – 3 = 4 → even
9 – 5 = 4 → even
Parity of result = even
∴ odd – odd = even
(f) even - odd =
Ans: Example:
8 – 3 = 5
12 – 5 = 7
Parity of result = odd
∴ even – odd = odd
(g) odd - even =
Ans: Example:
7 – 2 = 5
9 – 6 = 3
Parity of result = odd
∴ odd – even = odd
Small Squares in Grids
In a 3 × 3 grid, there are 9 small squares, which is an odd number. Meanwhile, in a 3 × 4 grid, there are 12 small squares, which is an even number.
Q1: Given the dimensions of a grid, can you tell the parity of the number of small squares without calculating the product?
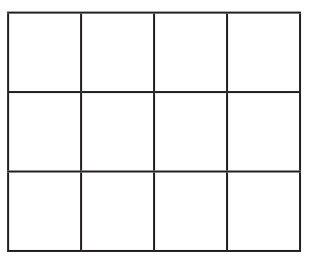 Ans: Yes, we can determine the parity of the number of small squares in a grid without directly calculating the full product, simply by observing the parity of the dimensions.
Ans: Yes, we can determine the parity of the number of small squares in a grid without directly calculating the full product, simply by observing the parity of the dimensions.
Rule: The product of two numbers is:
- Even if at least one of the numbers is even.
- Odd if both numbers are odd.
Page No. 132
Q1: Find the parity of the number of small squares in these grids:
(a) 27 × 13
Ans: Both 27 and 13 are odd numbers, and Odd × Odd = Odd.
So, the parity of the number of small squares is odd.
(b) 42 × 78
Ans: Both 42 and 78 are even numbers, and Even × Even = Even.
So, the parity of the number of small squares is even.
Since 3276 is even, the answer is even.
(c) 135 × 654
Ans: 135 is odd, 654 is even, and Odd × Even = Even.
So, the parity of the number of small squares is even.
Parity of Expressions
Consider the algebraic expression: 3n + 4. For different values of n, the expression has different parity:
Q1: Come up with an expression that always has even parity.
Ans: Examples: 2n, 4n + 2, 6n - 4. Any expression of the form 2k or 2k + even.
Q2: Come up with expressions that always have odd parity.
Ans: Examples: 2n + 1, 2n - 1, 4n + 3. Any expression of the form 2k + 1.
Q3: Come up with other expressions, like 3n + 4, which could have either odd or even parity.
Ans: Examples: 3n, n + 5, 5n + 2. Any expression where the coefficient of n is odd and the constant term affects parity based on n.
Q4: Are there expressions using which we can list all the even numbers? Hint: All even numbers have a factor of 2
Ans: Yes, 2n (n = 1, 2, 3, ...) lists all even numbers (2, 4, 6, ...).
Q5: Are there expressions using which we can list all odd numbers?
Ans: Yes, 2n - 1 (n = 1, 2, 3, ...) lists all odd numbers (1, 3, 5, ...).
Q6: What would be the nth term for multiples of 2? Or, what is the nth even number?
Ans: The nth even number is 2n.
Q7: What is the 100th odd number?
Ans: The 100th odd number is 2 × 100 - 1 = 199.
Page No. 133
Q1: Write a formula to find the nth odd number.
Ans: The nth odd number is 2n - 1.
Some Explorations in Grids
Observe this 3 × 3 grid. It is filled following a simple rule— use numbers from 1 – 9 without repeating any of them. There are circled numbers outside the grid.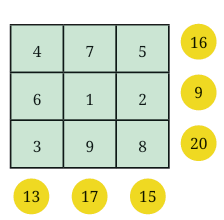
Q2: Are you able to see what the circled numbers represent?
Ans: The circled numbers represent the sums of the corresponding rows and columns in the 3×3 grid.
Q3: Fill the grids below based on the rule mentioned above: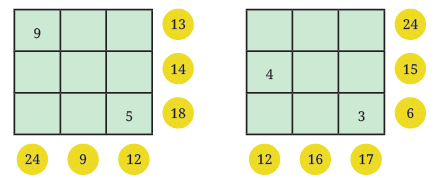
Ans: 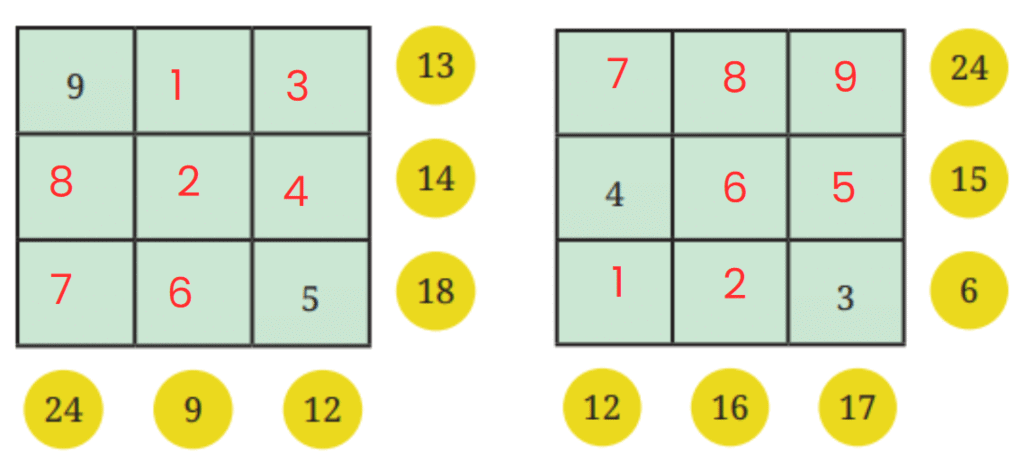
Page No. 134
Q: Make a couple of questions like this on your own and challenge your peers.
Ans: Do it Yourself!
Q: What can the magic sum be? Can it be any number?
Ans: The magic sum cannot be just any number. It is fixed for a 3 x 3 magic square and depends on the numbers being used.
For the numbers 1 to 9, the magic sum is 45.
Page No. 136
Q1: Can 1 occur in a corner position? For example, can it be placed as follows? If yes, then there should exist three ways of adding 1 to two other numbers to give 15. We have 1 + 5 + 9 = 15. Is any other combination possible?
Ans: Yes, 1 can be in a corner position. In the given example, 1 is in the top-left corner, and we have 1 + 5 + 9 = 15 along the diagonal. Let's check other ways:
- Row: 1 + (second number) + (third number) = 15
1 + 5 + (third number) = 15
1 + 5 = 6, so third number = 15 - 6 = 9. This matches the given grid. - Column: 1 + (second number) + (third number) = 15
1 + (second number) + 9 = 15
1 + 9 = 10, so second number = 15 - 10 = 5. This also matches.
Thus, it is possible for 1 to be in a corner.
Q2: Similarly, can 9 be placed in a corner position?
Ans: Do it Yourself!
Q3: Can you find the other possible positions for 1 and 9?
Ans: 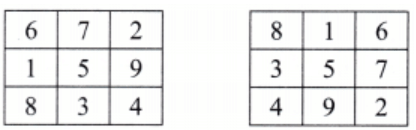
Figure it Out
Q1: How many different magic squares can be made using the numbers 1-9?
Ans: There are 8 distinct 3×3 magic squares using 1-9 (considering rotations and reflections as equivalent).
Q2. Create a magic square using the numbers 2-10. What strategy would you use for this? Compare it with the magic squares made using 1-9.
Ans: The numbers 2-10 are 9 consecutive numbers, just like 1-9, but increased by 1.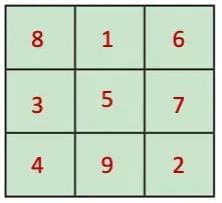
Strategy: Start with the classic 1-9 magic square, and add 1 to each number.
Original: After adding 1 to each: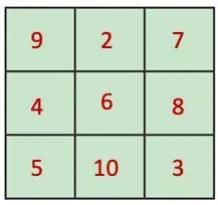
The magic square for numbers 2-10 would have a different magic sum (18) compared to numbers 1-9 (15). The structure remains similar, but the values are shifted up by 1.
Q3. Take a magic square, and
(a) increase each number by 1
Ans: After increasing each number by 1:
This is still a magic square.
New magic sum = 18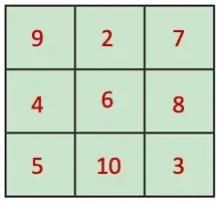
(b) double each number
Ans: After doubling each number
Still a magic square
New magic sum = 30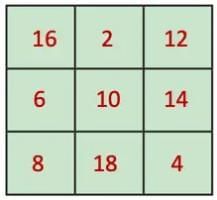
In each case, is the resulting grid also a magic square? How do the magic sums change in each case?
Ans: In case (a), adding a constant to every number, → magic sum increases by 3 × that constant.
In case (b), multiplying all by a constant → magic sum multiplied by that constant.
Q4. What other operations can be performed on a magic square to yield another magic square?
Ans: Add a constant, multiply by a constant, or reflect/rotate the grid.
Q5. Discuss ways of creating a magic square using any set of 9 consecutive numbers (like 2-10, 3-11, 9-17, etc.).
Ans: The magic square for numbers 2-10 can be seen in solution 2 above.
For the magic square using numbers 3-11, add 2 to each number in the original, and we get the adjoining magic square.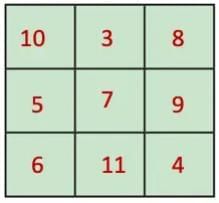
Here, magic sum = 21
For the magic square using numbers 9-17, add 8 to each number in the original, and we get a square as shown below.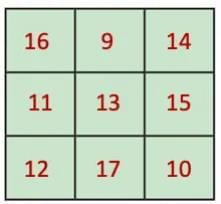
Here, magic sum = 39
Page No. 137
Q1: Choose any magic square that you have made so far using consecutive numbers. If m is the letter-number of the number in the centre, express how other numbers are related to m, how much more or less than m.
[Hint: Remember how we described a 2 × 2 grid of a calendar month in the Algebraic Expressions chapter].
Ans: For a magic square with centre m = 5:
Relative to m:
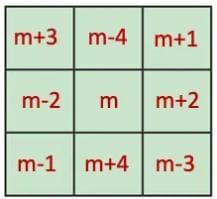
Once the generalised form is obtained, share your observations with the class.
Ans: Do it Yourself!
Figure it Out
Q1: Using this generalised form, find a magic square if the centre number is 25.
Ans: Magic sum = 3 × 25 = 75. Example: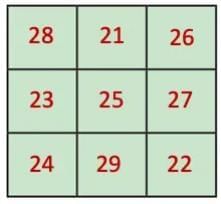
Q2: What is the expression obtained by adding the 3 terms of any row, column or diagonal?
Ans: Row sum (1st row) = 28 + 21 + 26 = 75
Column sum (1st column) = 28 + 23 + 24 = 75
Diagonal sum (1st column) = 28 + 25 + 22 = 75
The expression obtained = 3 × m
where m is the letter-number representing the number in the centre.
Q3: Write the result obtained by-
(a) adding 1 to every term in the generalised form.
(b) doubling every term in the generalised form
Ans:
(a) 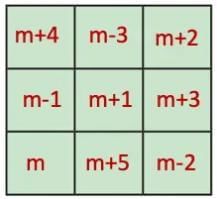 (b)
(b)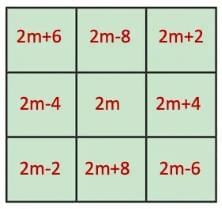
Q4: Create a magic square whose magic sum is 60.
Ans: Magic square with numbers 1-9 has a magic sum of 15.
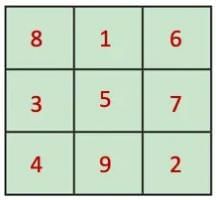
To get a magic square with a magic sum of 60, we need to multiply each number of the magic square 1-9 by 4. Therefore, a magic square with a magic sum of 60 is:
Q5: Is it possible to get a magic square by filling nine non-consecutive numbers?
Ans: Yes, it is possible.
Justification: Let us consider the two magic squares with a magic sum 45.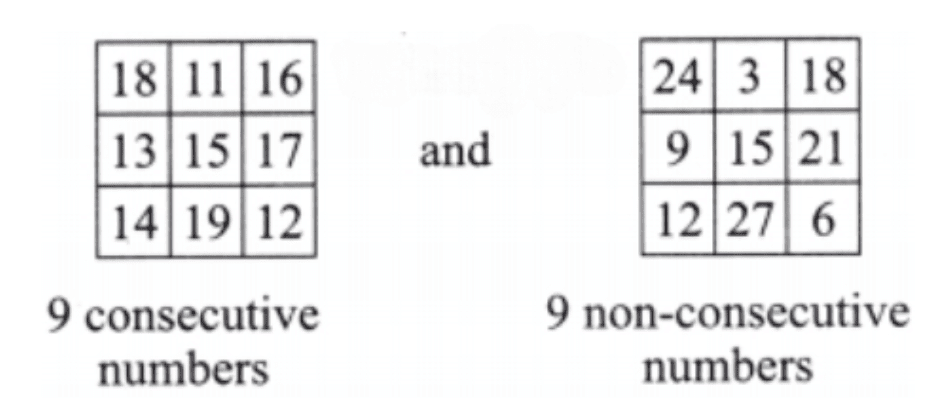
The First-ever 4 × 4 Magic Square
The first ever recorded 4 × 4 magic square is found in a 10th century inscription at the Pārśhvanath Jain temple in Khajuraho, India, and is known as the Chautīsā Yantra.
 Chautisā means 34. Why do you think they called it the Chautisā Yantra?
Chautisā means 34. Why do you think they called it the Chautisā Yantra?
Every row, column and diagonal in this magic square adds up to 34.
Can you find other patterns of four numbers in the square that add up to 34?
Ans: Yes, we can find different combinations of 4 numbers that add up 34 in the given square.
- Sum of 4 corner numbers: 7 + 14 + 4 + 9 = 34
- Sum of 4 central numbers: 13 + 8 + 10 + 3 = 34
- Sum of 4 numbers in any 2 × 2 squares:
- For example, top-left square: 7 + 12 + 13 + 2 = 34
Page No. 141
Q1: Use the systematic method to write down all 6-beat rhythms, i.e., write 6 as the sum of 1’s and 2’s in all possible ways. Did you get 13 ways?
Ans: Here n = 6
Write a ‘1+’ in front of all rhythms having 5 beats and then a ‘2+’ in front of all rhythms having 4 beats. This gives us all the rhythms having 6 beats.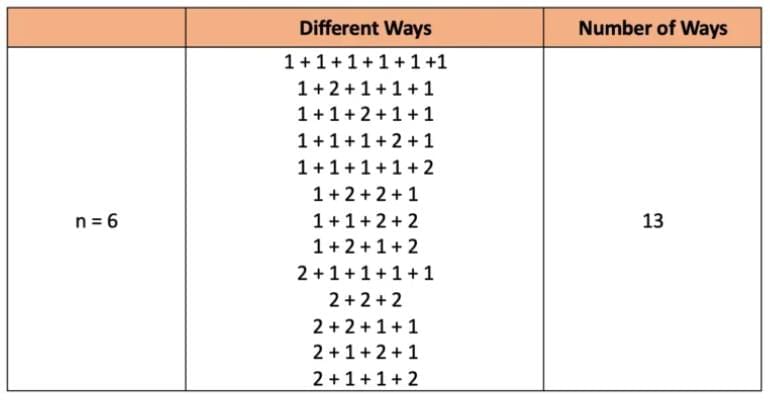
Yes, we get a total of 13 ways.
Page No. 142
Q1: Write the next number in the sequence, after 55.
Ans: 55 + 34 = 89.
Q2: Write the next 3 numbers in the sequence:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, _______,_______,_______,...
Ans: The next 3 terms in the sequence are:
55 + 89 = 144
89 + 144 = 233
144 + 233 = 377
Q3: If you have to write one more number in the sequence above, can you tell whether it will be an odd number or an even number (without adding the two previous numbers)?
Ans: To determine if the next number after 377 is odd or even without adding the previous terms, let’s examine the parity of the sequence.
Parity pattern: 1 (odd), 2 (even), 3 (odd), 5 (odd), 8 (even), 13 (odd), 21 (odd), 34 (even), 55 (odd), 89 (odd), 144 (even), 233 (odd), 377 (odd).
Q4: What is the parity of each number in the sequence? Do you notice any pattern in the sequence of parities?
Ans: Here, the parity alternates as follows:
odd, odd, even i.e., two odd numbers are followed by one even number.
So, the next number (after 377) will be even, as per the repeating parity cycle.
The pattern of parities: Repeats every 3 terms as Odd, Odd, Even.
Page No. 143
Let us look at one more example shown on the right.
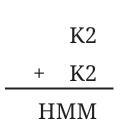
Here, K2 means that the number is a 2-digit number having the digit ‘2’ in the units place and ‘K’ in the tens place. K2 is added to itself to give a 3-digit sum HMM.
What digit should the letter M correspond to?
Both the tens place and the units place of the sum have the same digit.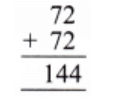
Q: What about H? Can it be 2? Can it be 3?
Ans: The possible value of two 2-digit numbers 72 with unit digit 2 is 72 + 72 = 144.
M corresponds to 4 and H corresponds to 1 in 144.
So, H cannot be 2 or 3.
Q. These types of questions can be interesting and fun to solve! Here are some more questions like this for you to try out. Find out what each letter stands for.
Share how you thought about each question with your classmates; you may find some new approaches.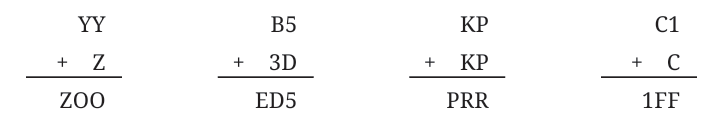
These types of questions are called ‘cryptarithms’ or ‘alphametics’.
Ans:
(i)
Here, Y = 9, Z = 1, and O = 0.
(ii)

Here, D = 0, B = 7 and E = 1.
(iii)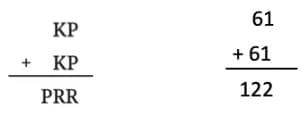
Here, K=6, P=1, R=2.
(iv)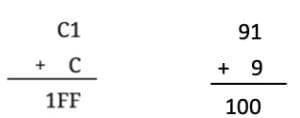 Here, C=9, F=0.
Here, C=9, F=0.
Figure it Out
Q1: A light bulb is ON. Dorjee toggles its switch 77 times. Will the bulb be on or off? Why?
Ans: Dorjee toggles the switch 77 times.
Each toggle changes the state of the bulb (ON to OFF or OFF to ON).
Starting from ON:
An odd number of toggles will leave the bulb OFF, and an even number of toggles will leave the bulb ON.
Since 77 is odd, after 77 toggles, the bulb will be OFF.
Q2: Liswini has a large old encyclopaedia. When she opened it, several loose pages fell out of it. She counted 50 sheets in total, each printed on both sides. Can the sum of the page numbers of the loose sheets be 6000? Why or why not?
Ans: Total sheets = 50
Each sheet has one even and one odd page number.
Thus, the total of 50 sheets consists of 50 even numbers and 50 odd numbers.
The sum of the even numbers is even. (because adding any number of even numbers is even).
The sum of the odd numbers is even. (because adding an even number of odd numbers is even).
Thus, the total sum is even + even = even.
Since 6000 is an even number, it is possible for the sum of the page numbers of the loose sheets to be 6000.
Q3: Here is a 2 × 3 grid. For each row and column, the parity of the sum is written in the circle: ‘e’ for even and ‘o’ for odd. Fill the 6 boxes with 3 odd numbers (‘o’) and 3 even numbers (‘e’) to satisfy the parity of the row and column sums.
Ans: Let’s label the cells as: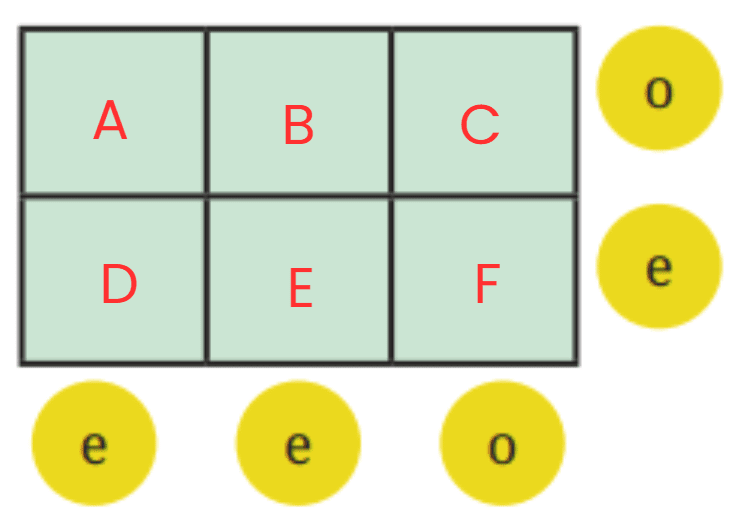
So the constraints are:
- Row 1 (A, B, C): sum is odd
- Row 2 (D, E, F): sum is even
- Column 1 (A, D): sum is even
- Column 2 (B, E): sum is even
- Column 3 (C, F): sum is odd
We’ll track parities only (o or e), not actual numbers.
Row 1: A = o, B = e, C = e, then o + e + e = odd
Column 1 (A, D) = e means A must be paired with D to get the sum as even.
So, if A = o, D = o, then o + o = even
Similarly, if B = e, E = e, then e + e = even
Again, if C = e, F = o, then e + o = odd
So, the 6 boxes with 3 odd numbers and 3 even numbers are as follows: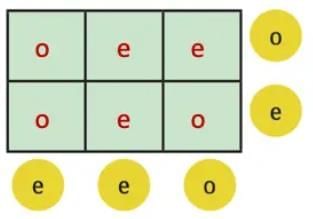
Q4: Make a 3 × 3 magic square with 0 as the magic sum. All numbers can not be zero. Use negative numbers, as needed.
Ans: It is given that
- The magic square is 3 × 3.
- The magic sum is 0.
- All numbers in the square cannot be zero; we can use negative numbers as needed.
So, we will use the numbers (-4) to 4 to create a magic square whose magic sum is 0.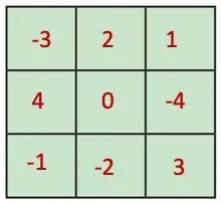
Q5: Fill in the following blanks with ‘odd’ or ‘even’:
(a) Sum of an odd number of even numbers is ______
(b) Sum of an even number of odd numbers is ______
(c) Sum of an even number of even numbers is ______
(d) Sum of an odd number of odd numbers is ______
Ans:
(a) Sum of odd number of even numbers is even.
(b) Sum of even number of odd numbers is even.
(c) Sum of even number of even numbers is even.
(d) Sum of odd number of odd numbers is odd.
Q6: What is the parity of the sum of the numbers from 1 to 100?
Ans: Sum = 1 + 2 + ... + 100 = 100 × 101 / 2 = 5050. Even (100 is even).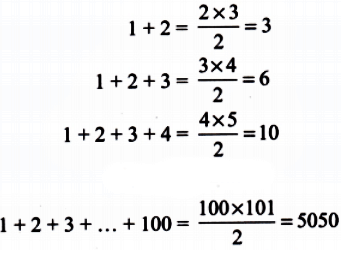 Q7: Two consecutive numbers in the Virahānka sequence are 987 and 1597. What are the next 2 numbers in the sequence? What are the previous 2 numbers in the sequence?
Q7: Two consecutive numbers in the Virahānka sequence are 987 and 1597. What are the next 2 numbers in the sequence? What are the previous 2 numbers in the sequence?
Ans: The given numbers are 987 and 1597.
In the Virahanka sequence, each number is the sum of the two preceding numbers.
The next two numbers are:
987 + 1597 = 2584
1597 + 2584 = 4181
The previous two numbers are:
1597 – 987 = 610
987 – 610 = 377
The sequence is …..,377, 610, 987, 1597, 2584, 4181,…..
Q8: Angaan wants to climb an 8-step staircase. His playful rule is that he can take either 1 step or 2 steps at a time. For example, one of his paths is 1, 2, 2, 1, 2. In how many different ways can he reach the top?
Ans: Ways in which Angaan can climb 8 steps with 1 or 2 steps are as follows:
For n = 8
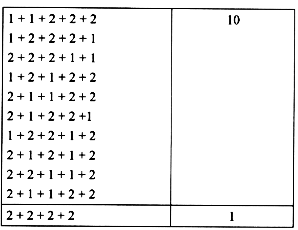
So, the total ways in which Angaan reaches the top = 1 + 7 + 15 + 10 + 1 = 34 ways.
Q9: What is the parity of the 20th term of the Virahānka sequence?
Ans:Consider the Virahanka sequence given below:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,…..
Let us observe the pattern of odd/even in Virahanka numbers given above:
Here 1 → odd
2 → even
3 → odd
5 → odd
8 → even
13 → odd
21 → odd
34 → even
So parity cycle is: odd, even, odd, (repeats every 3 terms)
So the 20th term of the Virahanka sequence is even.
Q10: Identify the statements that are true.
(a) The expression 4m - 1 always gives odd numbers.
Ans: Substituting m = 1 in 4m – 1 = 4 × 1 – 1 = 3 (odd).
Substituting m = 2 in 4m – 1= 4 × 2 – 1 = 7 (odd).
Thus, the expression 4m – 1 always gives odd numbers.
This statement is true.
(b) All even numbers can be expressed as 6j - 4.
Ans: Substituting j = 1 in 6j – 4 = 6 × 1 – 4 = 2 (even).
Substituting j = 2 in 6j – 4 = 6 × 2 – 4 = 8 (even).
This expression produces even numbers, but it does not produce all even numbers (for e.g., it skips 4 and 6).
This statement is false.
(c) Both expressions 2p + 1 and 2q - 1 describe all odd numbers.
Ans: Substituting p = 1, 2, 3,….. in 2p + 1, we get 3, 5, 7,…..
Substituting q = 1, 2, 3,…. in 2q + 1, we get 1, 3, 5, 7,…….
Here, 2q – 1 describes all the odd numbers but 2p + 1 does not describe 1.
Thus, this statement is false.
(d) The expression 2f + 3 gives both even and odd numbers.
Ans: Substituting f = 1, 2f + 3 = 2 × 1 + 3 = 5 (odd).
Substituting f = 2, 2f + 3 = 2 × 2 + 3 = 7 (odd).
The expression 2f + 3 always gives odd numbers because 2f is even and adding 3 makes it odd.
This statement is false.
Q11: Solve this cryptarithm: 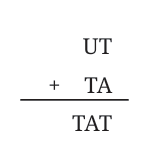 Ans: Here, T is at hundreds place, so T = 1
Ans: Here, T is at hundreds place, so T = 1
⇒ A = 0 and U = 9.
So, we have U = 9, T = 1, and A = 0.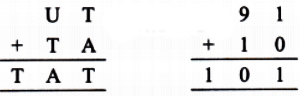
|
41 videos|251 docs|8 tests
|
FAQs on NCERT Solutions for Class 7 Maths Chapter 6 Number Play
| 1. What is the importance of learning number play in Class 7? |  |
| 2. How can I improve my skills in number play? |  |
| 3. What types of questions can I expect in exams related to number play? |  |
| 4. Are there any specific strategies for solving number play problems? |  |
| 5. How can parents assist their children in mastering number play? |  |
















