NCERT Solutions for Class 7 Maths Chapter 5 Parallel and Intersecting Lines
| Table of contents |

|
| Page No. 106 |

|
| Page No. 107 |

|
| Page No. 108 |

|
| Page No. 110 |

|
| Page No. 111 |

|
| Page No. 112 |

|
| Page No. 113 |

|
| Page No. 114 |

|
| Page No. 115 |

|
| Page No. 119 & 120 |

|
| Page 123 |

|
| Page No. 125 |

|
Page No. 106
Take a piece of square paper and fold it in different ways. Now, on the creases formed by the folds, draw lines using a pencil and a scale. You will notice different lines on the paper. Take any pair of lines and observe their relationship with each other. Do they meet? If they do not meet within the paper, do you think they would meet if they were extended beyond the paper?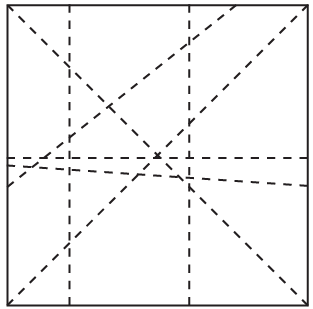 Ans: Some pairs of lines meet at a point on the paper, forming intersecting lines. Others do not meet within the paper. If extended beyond the paper, some non-meeting lines may intersect outside the paper, while others, if parallel, will never meet.
Ans: Some pairs of lines meet at a point on the paper, forming intersecting lines. Others do not meet within the paper. If extended beyond the paper, some non-meeting lines may intersect outside the paper, while others, if parallel, will never meet.
Let us observe what happens when two lines intersect.
Q: How many angles do they form?
Ans: When two lines intersect, they form four angles.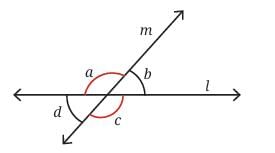
Page No. 107
Q: Can two straight lines intersect at more than one point?
Ans: No, two straight lines can only intersect at one point. If they are parallel, they never intersect. But if two lines appear to intersect at more than one point, it means they are the same.
Activity 1: Draw two lines on a plain sheet of paper so that they intersect. Measure the four angles formed with a protractor. Draw four such pairs of intersecting lines and measure the angles formed at the points of intersection.
Ans: 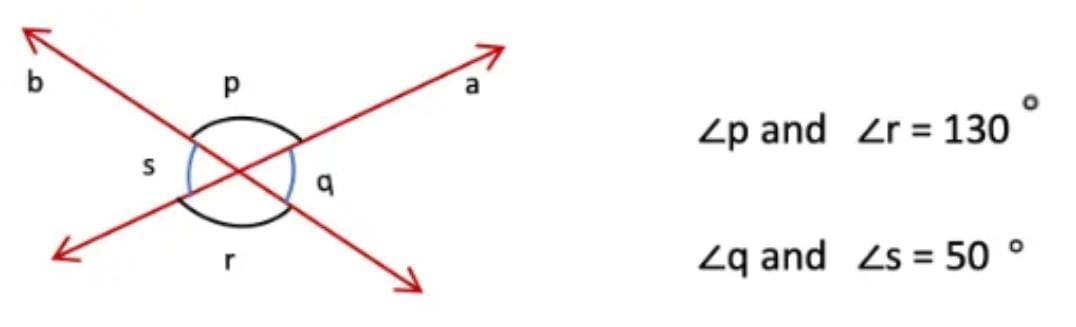
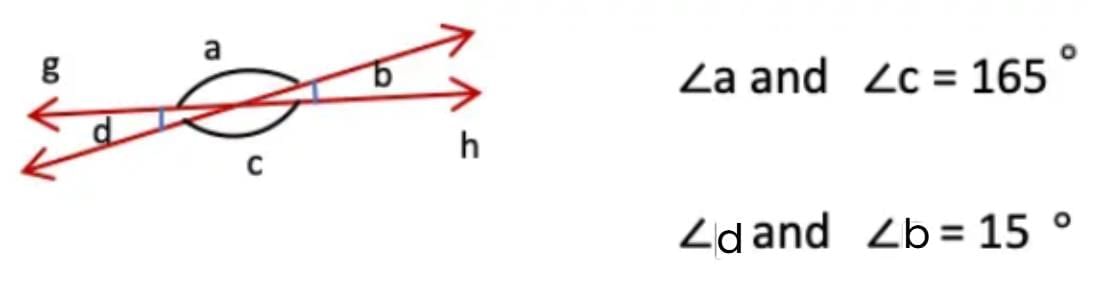
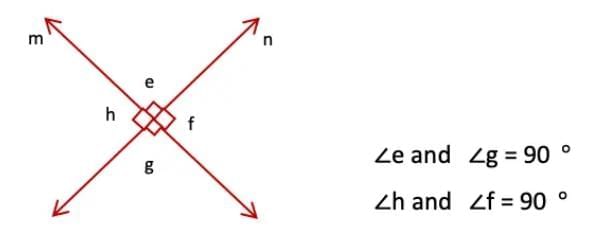
Q: What patterns do you observe among these angles?
Ans: The patterns we observed among these angles are:
Vertically opposite angles are equal:
For example, in the figure, ∠a = ∠c and ∠b = ∠d.
Linear pairs add up to 180°:
Adjacent angles like ∠a + ∠b or ∠b + ∠c form a straight angle, which means their sum is always 180°.
These patterns are true for any pair of intersecting lines and form the basis of angle relationships in geometry.
Q: In given figure, if ∠a is 120°, can you figure out the measurements of ∠b, ∠c, and ∠d, without drawing and measuring them?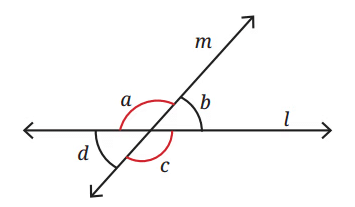 Ans: ∠b = 180° - ∠a
Ans: ∠b = 180° - ∠a
= 180° - 120° = 60° (linear pair).
∠c = ∠a = 120° (vertically opposite).
∠d = ∠b = 60° (vertically opposite).
Is this always true for any pair of intersecting lines?
Ans: Yes. When two lines intersect, they form four angles at a point of intersection. The angles directly opposite each other at this point are called vertically opposite angles, and they are always equal in measure.
Page No. 108
Figure it Out
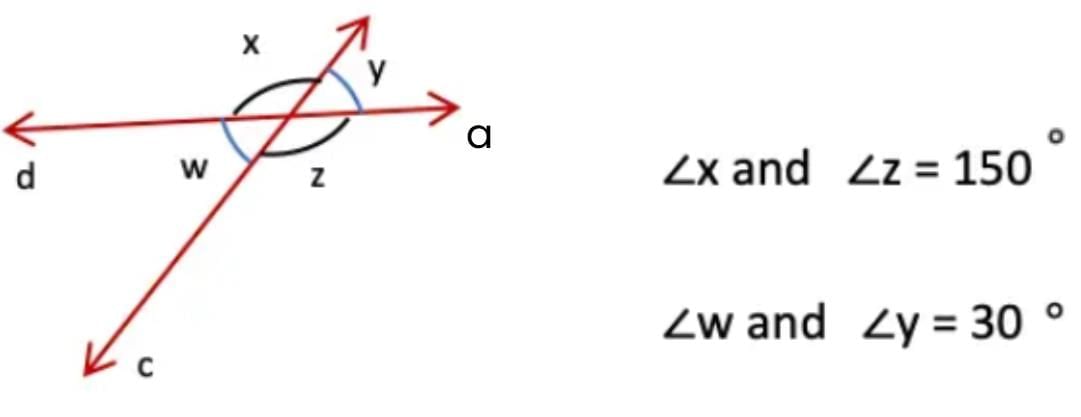
Q1: List all the linear pairs and vertically opposite angles you observe in Fig. 5.3: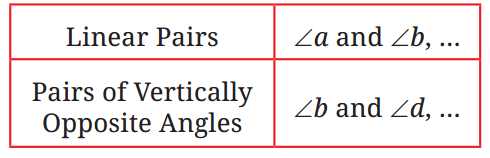
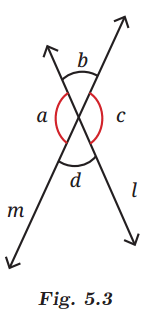 Ans: Linear Pairs: These are angles that are adjacent and form a straight line (add up to 180°).
Ans: Linear Pairs: These are angles that are adjacent and form a straight line (add up to 180°).
- ∠a and ∠b
- ∠b and ∠c
- ∠c and ∠d
- ∠d and ∠a
Vertically Opposite Angles: These are angles that are opposite each other when two lines intersect (they are equal).
- ∠b and ∠d (they are opposite each other at the intersection).
- ∠a and ∠c (they are opposite each other at the intersection).
Page No. 110
Observe given figure below and describe the way the line segments meet or cross each other in each case, with appropriate mathematical words (a point, an endpoint, the midpoint, meet, intersect) and the degree measure of each angle.
For example, line segments FG and FH meet at the endpoint F at an angle 115.3°.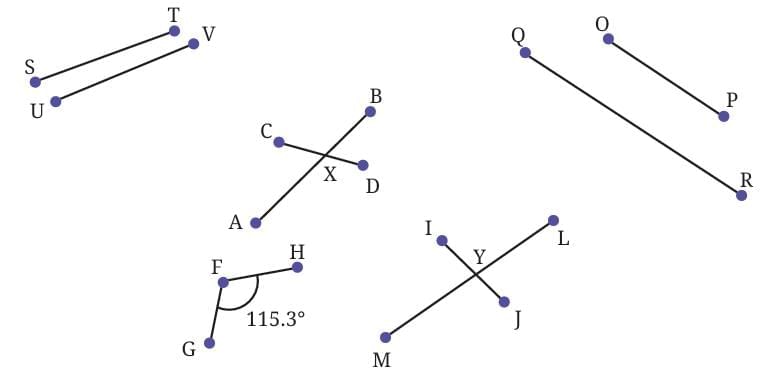
Are line segments ST and UV likely to meet if they are extended?
Ans: If the lines are not parallel, they will likely intersect at some point. Thus, line segments ST and UV are likely to meet when extended, as they are not parallel.
Are line segments OP and QR likely to meet if they are extended?
Ans: If two lines are parallel, they will never meet, regardless of how far they are extended. Thus, line segments OP and QR didn’t meet when extended, as they are parallel.
Q: Which pairs of lines appear to be parallel in Fig. 5.6 below?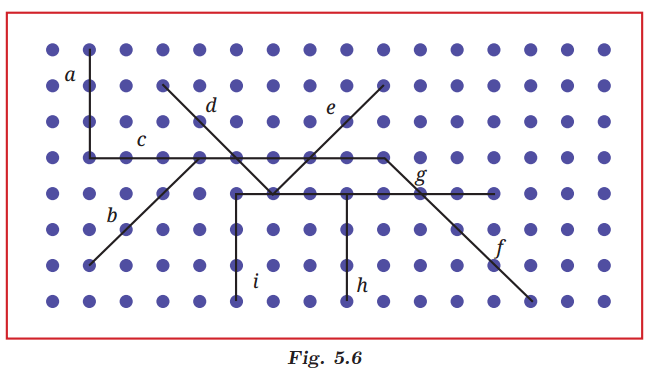 Ans: Two lines are said to be parallel when they do not meet at any point.
Ans: Two lines are said to be parallel when they do not meet at any point.
Here, lines a, i, and h are parallel to each other;
Line c is parallel to line g;
Line d is parallel to line f;
Line e is parallel to line b.
Page No. 111
Activity 2: Take a plain square sheet of paper (use a newspaper for this activity). 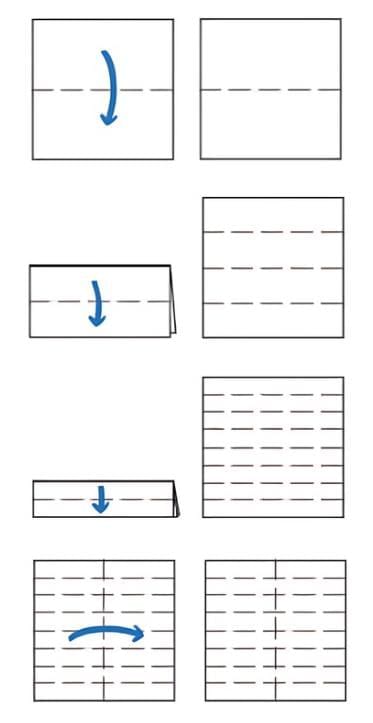 Q1: How would you describe the opposite edges of the sheet? They are __________to each other.
Q1: How would you describe the opposite edges of the sheet? They are __________to each other.
Ans: The opposite edges of the sheet are parallel to each other.
Q2: How would you describe the adjacent edges of the sheet? The adjacent edges are __________ to each other. They meet at a point. They form right angles.
Ans: The adjacent edges are perpendicular to each other. They meet at a point and form right angles (90°).
Q3: Fold the sheet horizontally in half. A new line is formed.
Ans: The two original top/bottom edges and the new horizontal fold.
Q4: How many parallel lines do you see now? How does the new line segment relate to the vertical sides?
Ans: We see three parallel horizontal lines — the top edge, the fold, and the bottom edge. The new horizontal line is perpendicular to the vertical sides.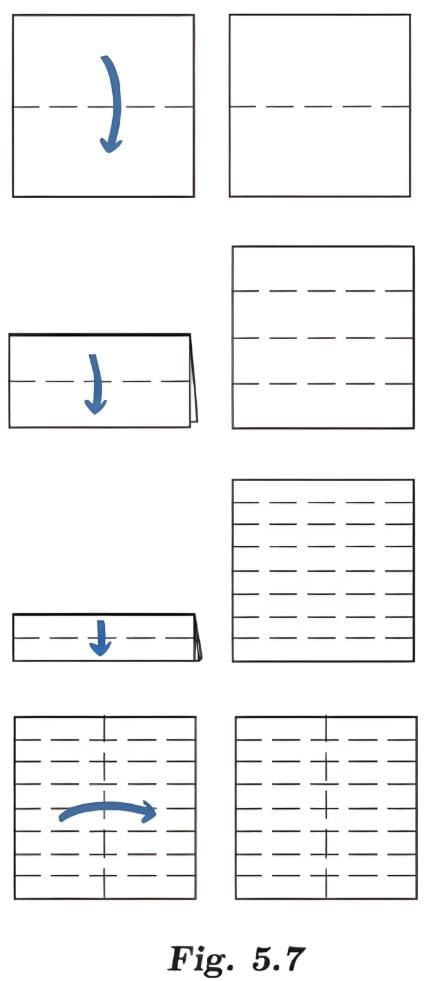
Q5: Make one more horizontal fold in the folded sheet. How many parallel lines do you see now?
Ans: After another horizontal fold, there are 5 parallel lines (the two original edges plus the three horizontal folds).
The pattern relates to powers of 2; after n folds, we have 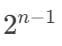 fold lines, plus the 2 original edges for
fold lines, plus the 2 original edges for 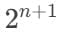 total parallel lines (starting from n =1 fold).
total parallel lines (starting from n =1 fold).
We can check if the pattern continues.
Q7: Make a vertical fold in the square sheet. This new vertical line is to the previous horizontal lines.
Ans: The new vertical line is perpendicular to the previous horizontal lines.
Q8: Fold the sheet along a diagonal. Can you find a fold that creates a line parallel to the diagonal line?
Ans: This requires performing the activity. It is possible to create such a fold (e.g., by folding an edge onto the diagonal or folding the paper in half parallel to the first diagonal fold).
Page No. 112
Here is another activity for you to try.
• Take a square sheet of paper, fold it in the middle and unfold it.
• Fold the edges towards the centre line and unfold them.
• Fold the top right and bottom left corners onto the creased line to create triangles.
• The triangles should not cross the crease lines.
• Are a, b and c parallel to p, q and r respectively? Why or why not?
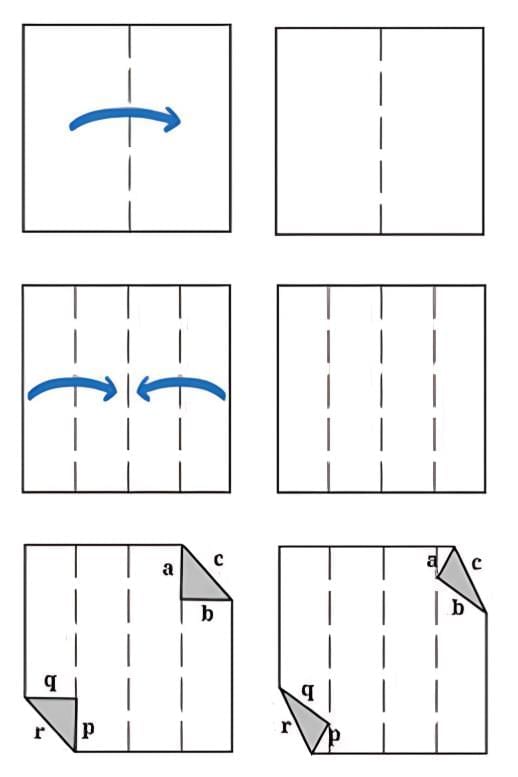 Ans: Yes, a, b, and c are parallel to p, q, and r, respectively in Figure A.
Ans: Yes, a, b, and c are parallel to p, q, and r, respectively in Figure A.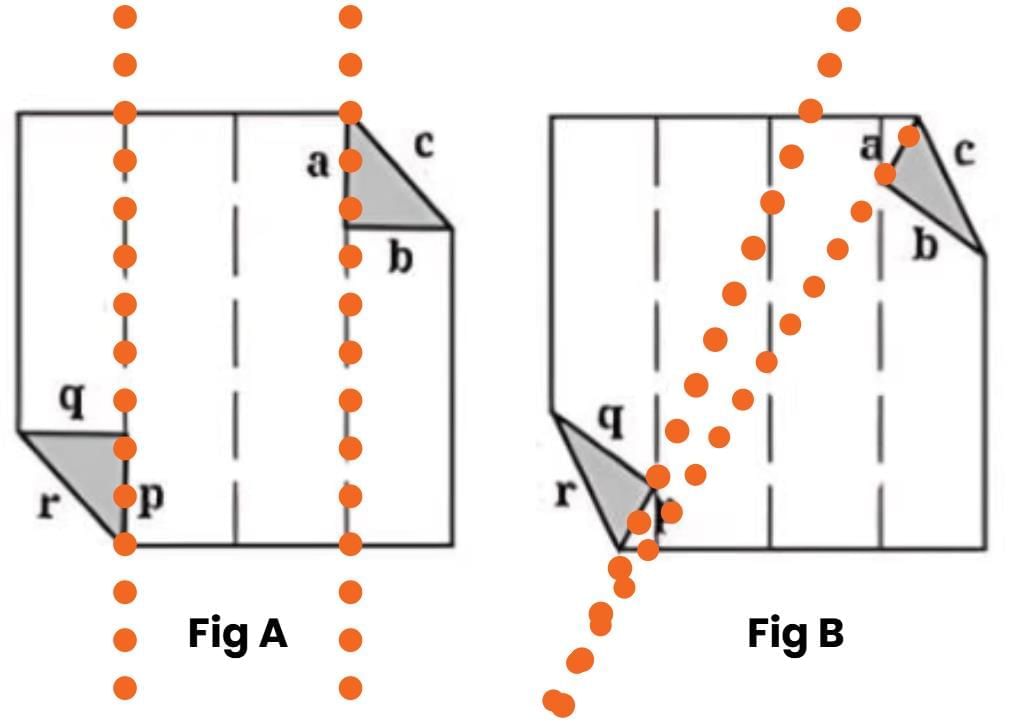
But in Figure B, they are not parallel.
Lines a, b and c are vertical crease lines running from top to bottom of the paper. Lines p, q and r are the diagonal edges of the triangular folds created when we fold the corners. Since the crease lines run vertically and the triangle edges run diagonally, they intersect each other rather than being parallel.
Page No. 113
Figure it Out
Q1: Draw some lines perpendicular to the lines given on the dot paper in Fig. 5.10.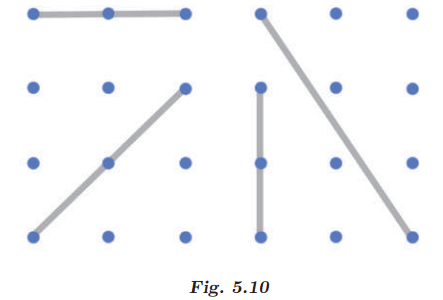 Ans:
Ans: 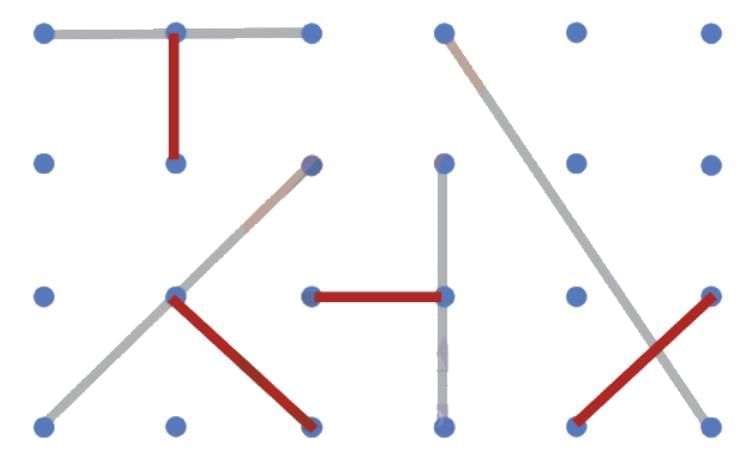
Q2: In Fig. 5.11, mark the parallel lines using the notation given above (single arrow, double arrow etc.). Mark the angle between perpendicular lines with a square symbol.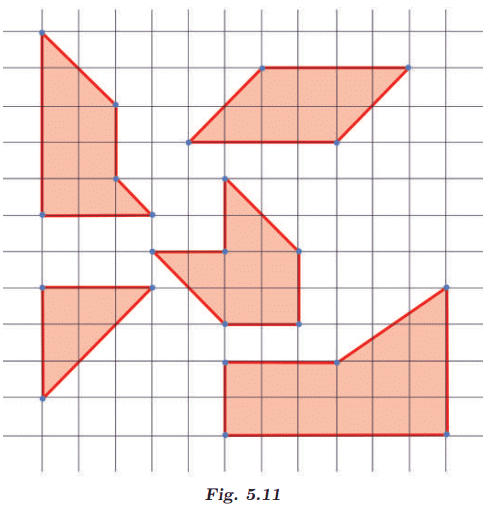 (a) How did you spot the perpendicular lines?
(a) How did you spot the perpendicular lines?
Ans: To spot perpendicular lines in a geometric figure, observe if lines intersect at a 90° angle.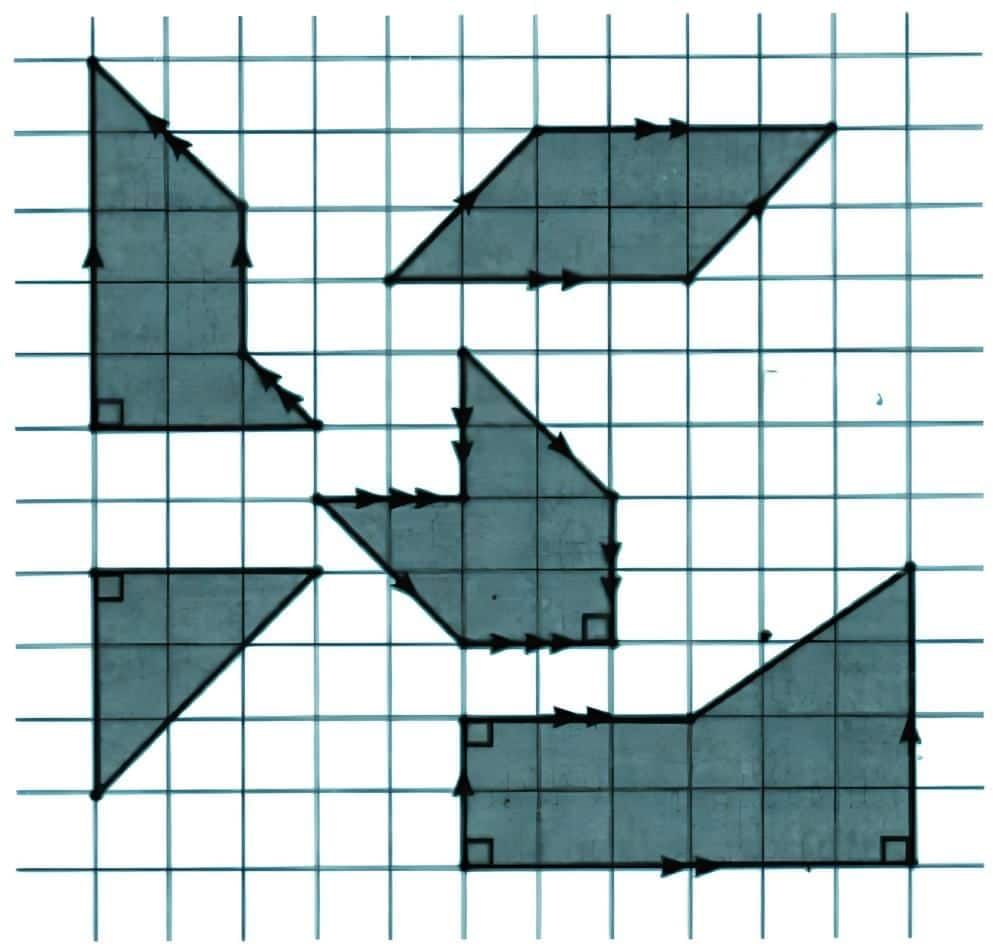
(b) How did you spot the parallel lines?
Ans: To spot parallel lines in a geometric figure, observe if lines never intersect at any point.
Q3: In the dot paper following, draw different sets of parallel lines. The line segments can be of different lengths but should have dots as endpoints.
Ans: Do it yourself.
Page No. 114
Q4: Using your sense of how parallel lines look, try to draw lines parallel to the line segments on this dot paper.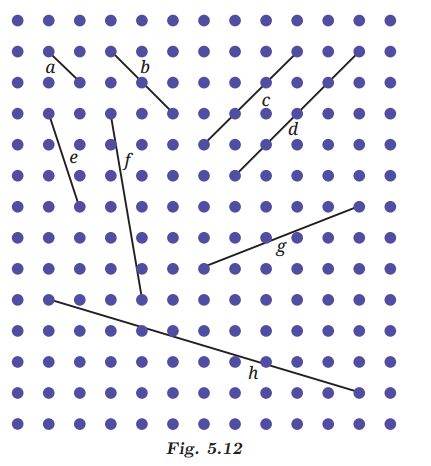 (a) Did you find it challenging to draw some of them?
(a) Did you find it challenging to draw some of them?
(b) Which ones?
(c) How did you do it?
Ans:
(a) Yes, some line segments are a little more difficult to draw than others.
(b) Line segments e, f, h, and g.
(c) Parallel lines are drawn by keeping them equidistant from the given lines.
Q5: In Fig. 5.13, which line is parallel to line a - line b or line c? How do you decide this?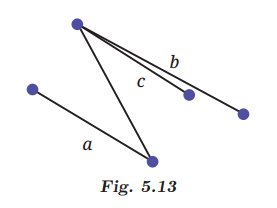 Ans: In the given figure, line a is parallel to line c because these two lines are always the same distance apart and never meet, no matter how far they go.
Ans: In the given figure, line a is parallel to line c because these two lines are always the same distance apart and never meet, no matter how far they go.
Page No. 115
In Fig. 5.14, line t intersects lines l and m, t is called a transversal. Notice that 8 angles are formed when a line crosses a pair of lines.
Q: Is it possible for all the eight angles to have different measurements? Why, why not?
Ans: No, all eight angles cannot have different measurements. Vertically opposite angles are equal, so there are at most four distinct angle measures.
Q: What about five different angles - 6, 5, 4, 3, and 2?
Ans: Five different angles are not possible, as vertically opposite angles must be equal, limiting the number of distinct angles to four.
Page No. 119 & 120
Figure it Out
Q: Can you draw a line parallel to l, that goes through point A? How will you do it with the tools from your geometry box? Describe your method. Ans: Tools Needed:
Ans: Tools Needed:
- Ruler
- Set Squares (right-angled triangle)
- Pencil
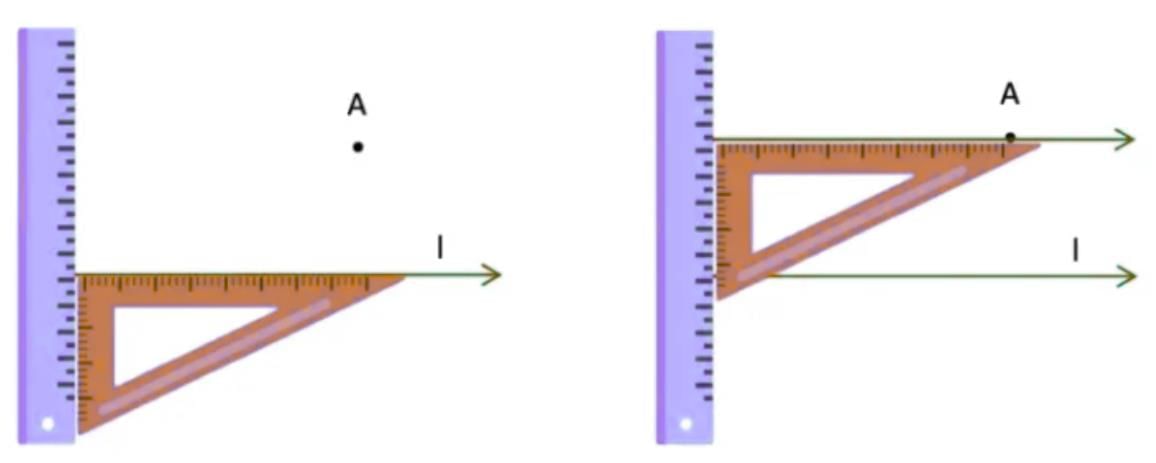
Step-by-Step Procedure:
- Place the set square so that one side is along the line l.
- Hold the ruler against the other side of the set square (the ruler won’t move).
- Slide the set square along the ruler until one side reaches point A.
- Draw a line along the edge of the set square through point A.
- This new line is parallel to line l and passes through point A.
Making Parallel Lines through Paper Folding
Let us try to do the same with paper folding. For a line l (given as a crease), how do we make a line parallel to l such that it passes through point A?
We know how to fold a piece of paper to get a line perpendicular to l. Now, try to fold a perpendicular to l such that it passes through point A. Let us call this new crease t.
Now, fold a line perpendicular to t passing through A again. Let us call this line m. The lines l and m are parallel to each other. l 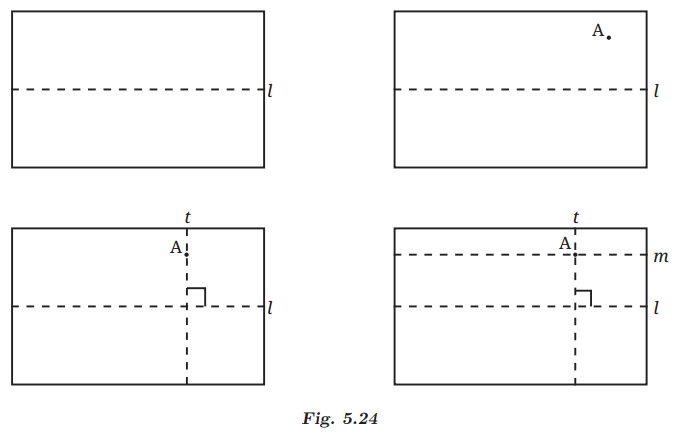
Q: Why are lines l and m parallel to each other?
Ans: Line t is perpendicular to line l; line m is also perpendicular to line t. Thus, if two lines are perpendicular to the same line, they are parallel to each other. Thus, lines l and m are parallel to each other because they share the same perpendicular relationship with line t.
Page 123
Figure it Out
Q1: Find the angles marked below.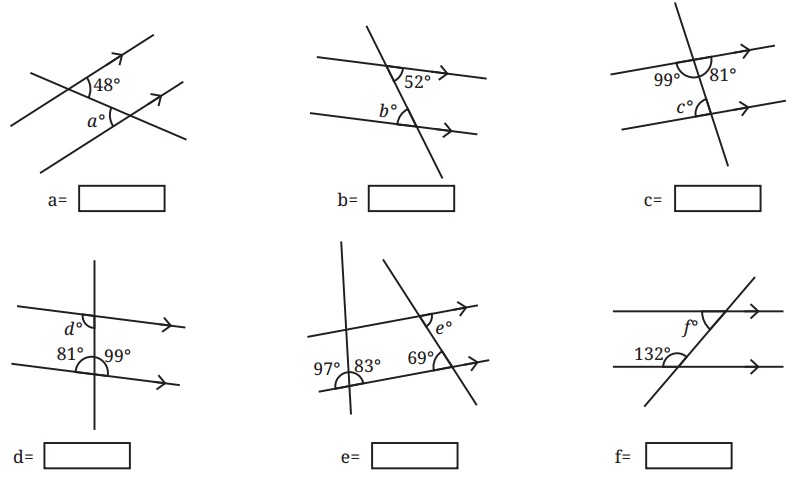
Ans:
(a) Find the angle marked in figure a.
Ans: Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, a = 48°
(b) Find the angle marked in figure b.
Ans: Since alternate angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, b = 52°.
(c) Find the angle marked in figure c.
Ans: The sum of the interior angles on the same side of the transversal always adds up to 180°. So, 180° – 99° = 81°. Therefore, c = 81°.
(d) Find the angle marked in figure d.
Ans: The sum of the interior angles on the same side of the transversal always adds up to 180°. So, 180° – 81° = 99°. Therefore, d = 99°
(e) Find the angle marked in figure e.
Ans: Alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, e = 69°.
(f) Find the angle marked in figure f.
Ans: The sum of the interior angles on the same side of the transversal always adds up to 180°. So, 180°- 132° = 48°. Therefore, f = 48°.
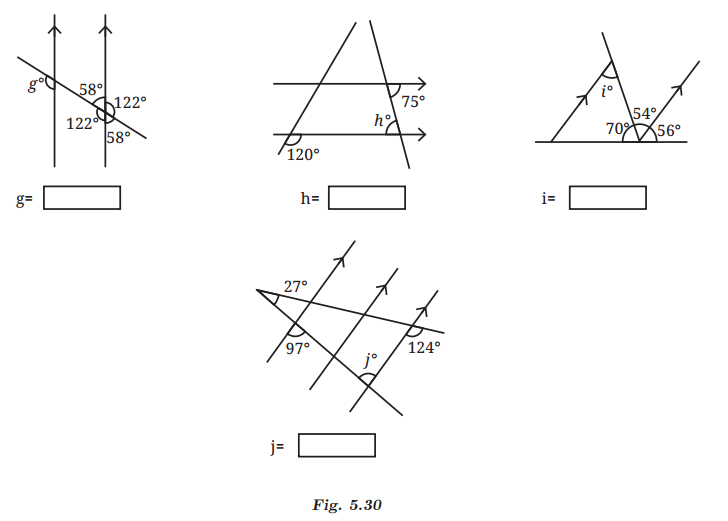
(g) Find the angle marked in figure g.
Ans: Corresponding angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, g = 122°.
(h) Find the angle marked in figure h.
Ans: Since alternate interior angles formed by a transversal intersecting a pair of parallel lines are equal, angle h is 75°.
(i) Find the angle marked in figure i.
Ans: Alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, i = 54°.
(j) Find the angle marked in figure j.
Ans: Alternate interior angles formed by a transversal intersecting a pair of parallel lines are always equal to each other. Therefore, j = 97°.
Q2: Find the angle represented by a.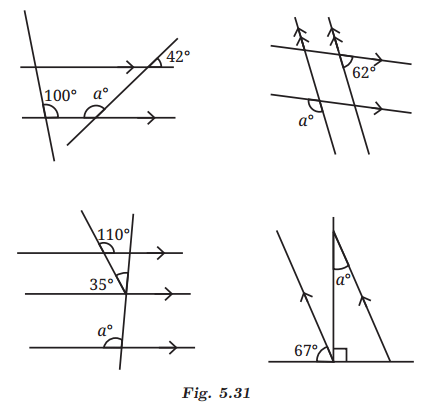 Ans:
Ans: 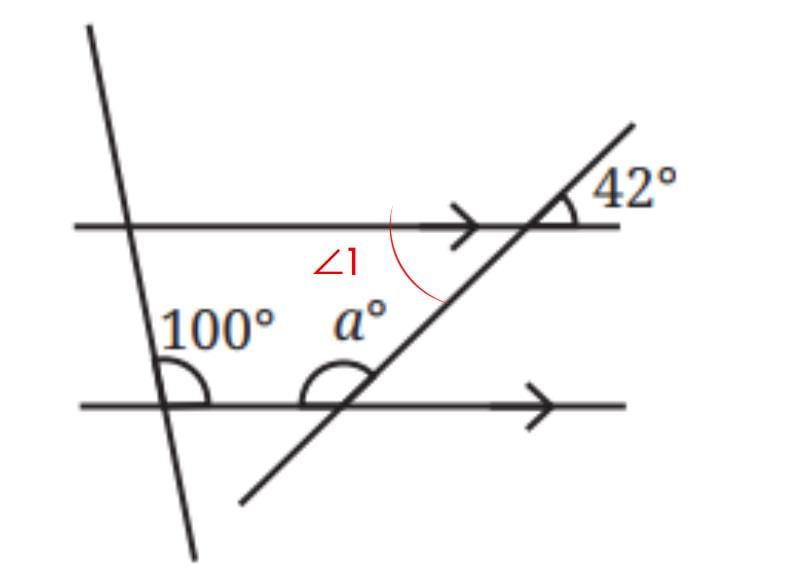
Sol: ∠1 = 42° ( Vertically opposite angles)
42° + a° = 180° ( Sum of interior angles on the same side of the transversal)
⇒ a° = 180° - 42°
⇒ a° = 138°
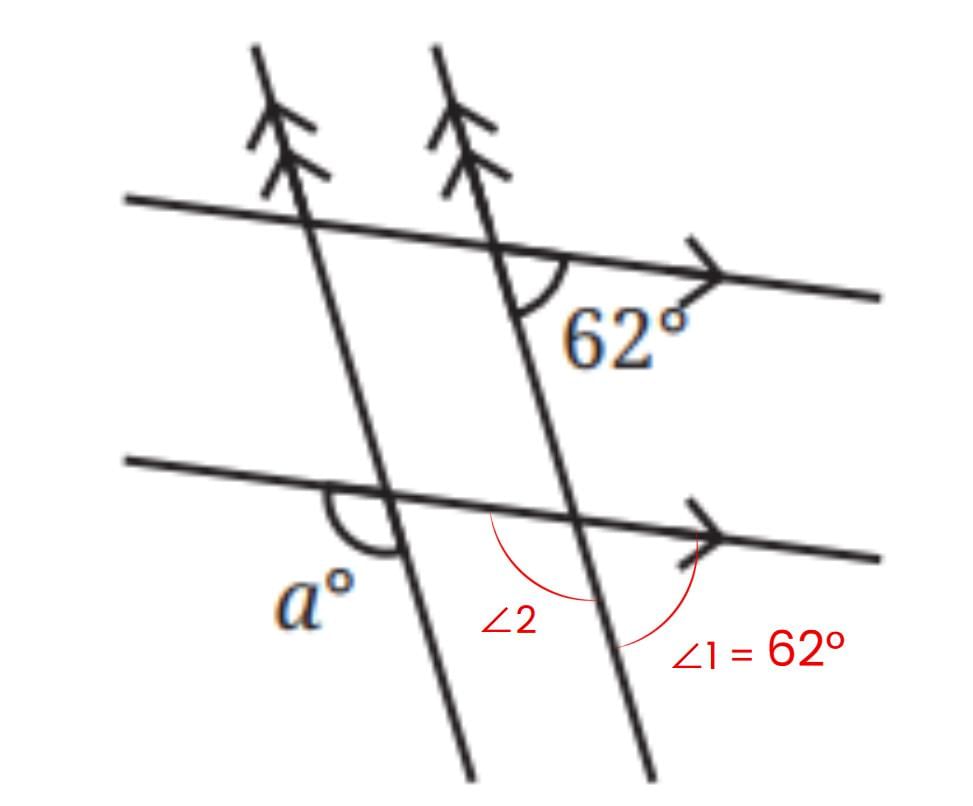
Sol: ∠1 = 62° (Corresponding angles are equal)
∠1 + ∠2 = 180° ( Linear Pair)
⇒ 62° + ∠2 = 180°
⇒ ∠2 = 118°
Now, a° = 118° (Corresponding angles are equal)
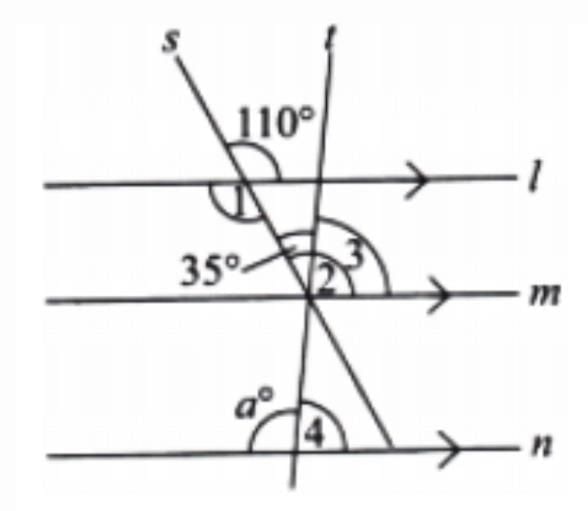
Sol: Here, lines s and l are intersecting lines.
So, ∠1 = 110° [Vertically opposite angles]
And ∠1 = ∠2 = 110° because lines l and m are parallel and line s is a transversal.
Therefore ∠3 = ∠2 – 35° = 110° – 35° = 75°
Also, ∠3 = ∠4 = 75° [Corresponding angles]
So, a° = 180° – 75° = 105° [Linear pair angles]
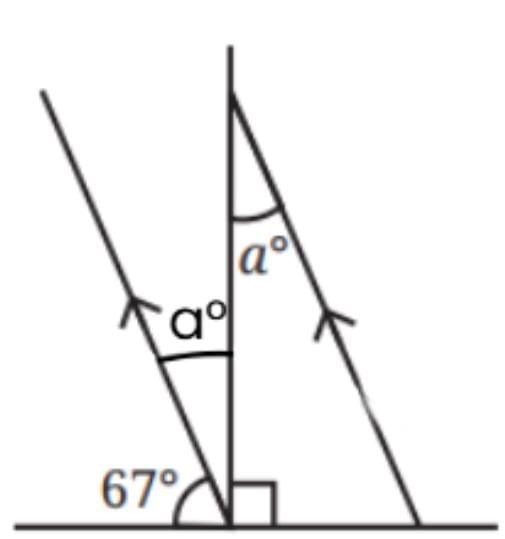
Sol: ⇒ 67° + aº + 90° = 180° ( Using angles on a straight line)
⇒ a°= 23° ( Also, alternate angles are equal).
Q3: In the figures below, what angles do x and y stand for in Fig. 5.32?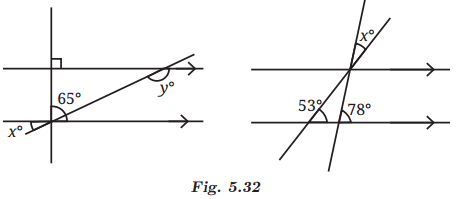 Ans: In Fig. 5.32 (left), there is the correction in the image.
Ans: In Fig. 5.32 (left), there is the correction in the image.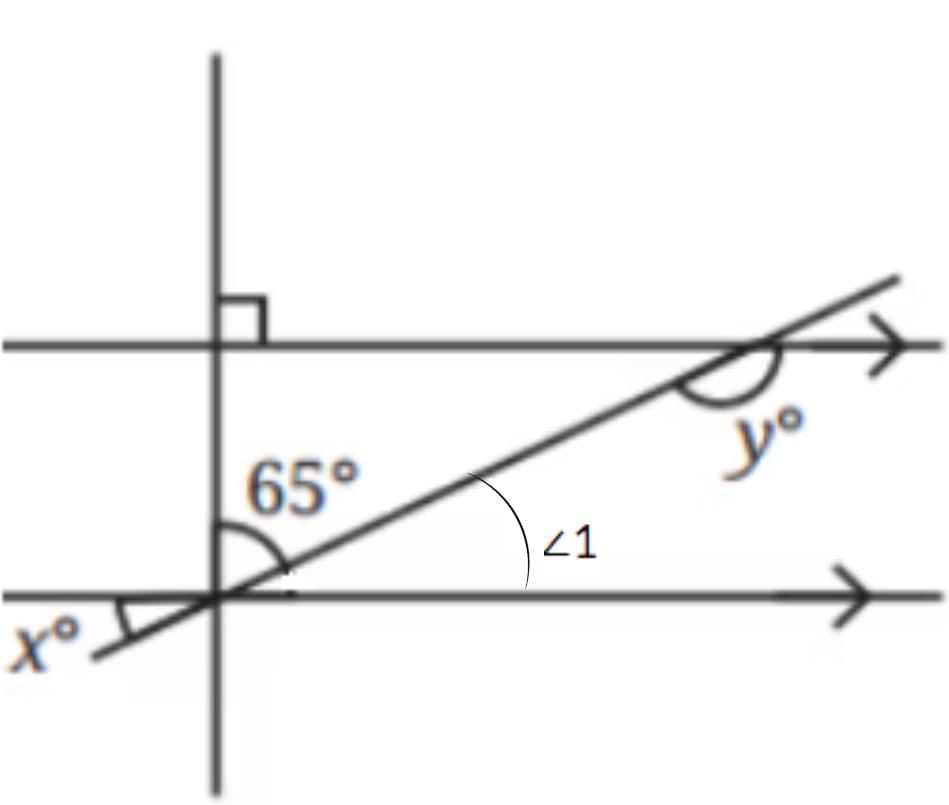
∠1 = xº ( Alternate angles)
∠1 + 65° = 90° ( Linear Pair)
⇒ xº + 65° = 90°
⇒ xº = 25°
∠1+ y = 180° (Sum of interior angles on the same side of the transversal)
xº + y = 180°
⇒ y = 180° - 25° = 155°
In Fig. 5.32 (right), 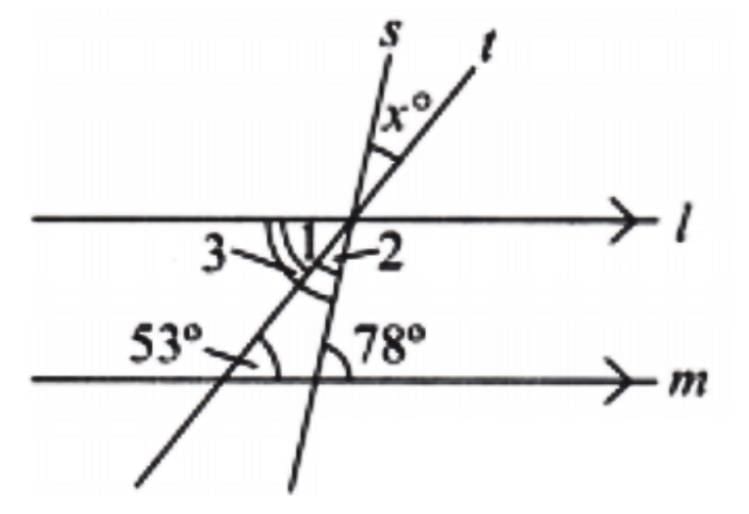
Since lines l and m are parallel and line s is a transversal.
So, ∠3 = 78° [Alternate Angles]
Also, lines l and m are parallel, and line t is a transversal.
So, ∠1 = 53° [Alternate Angles]
Therefore, ∠2 = ∠3 – ∠1 = 78° – 53° = 25°
Lines s and t are intersecting lines.
Therefore, x° = ∠2 = 25° [ Vertically Opposite Angles]
Q4: In Fig. 5.33, ∠ABC = 45° and ∠IKJ = 78°. Find angles ∠GEH, ∠HEF, ∠FED.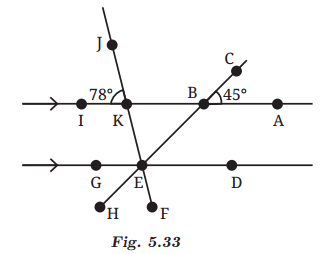 Ans: Line segments IA and HC intersect at point B.
Ans: Line segments IA and HC intersect at point B.
So, ∠ABC = ∠KBE = 45° [Vertically Opposite Angles]
Similarly, line segments JF and IA intersect at point K.
So, ∠IKJ = ∠BKE = 78° [Vertically Opposite Angles]
∠KBE = ∠GEH = 45° [Corresponding Angles]
Similarly, ∠BKE = ∠FED = 78° [Corresponding Angles]
Now, ∠GEH + ∠HEF + ∠FED = 180° [Linear Pair]
∠HEF = 180° – 45° – 78° = 57°
Page No. 125
Q5: In Fig. 5.34, AB is parallel to CD and CD is parallel to EF. Also, EA is perpendicular to AB. If ∠BEF = 55°, find the values of x and y. Ans: Given AB is parallel to CD and CD is parallel to EF.
Ans: Given AB is parallel to CD and CD is parallel to EF.
So, AB is parallel to EF.
Now, EF is parallel to CD, and DE is a transversal.
So, y° + 55° = 180° [Sum of interior angles on the same side of the transversal]
y = 125°
Now, AB is parallel to CD, and BD is a transversal.
So, x° = y° = 125° [Corresponding Angles]
Q6: What is the measure of angle ∠NOP in Fig. 5.35? [Hint: Draw lines parallel to LM and PQ through points N and O.]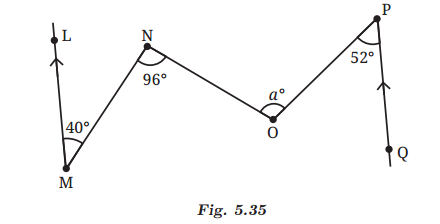 Ans:
Ans: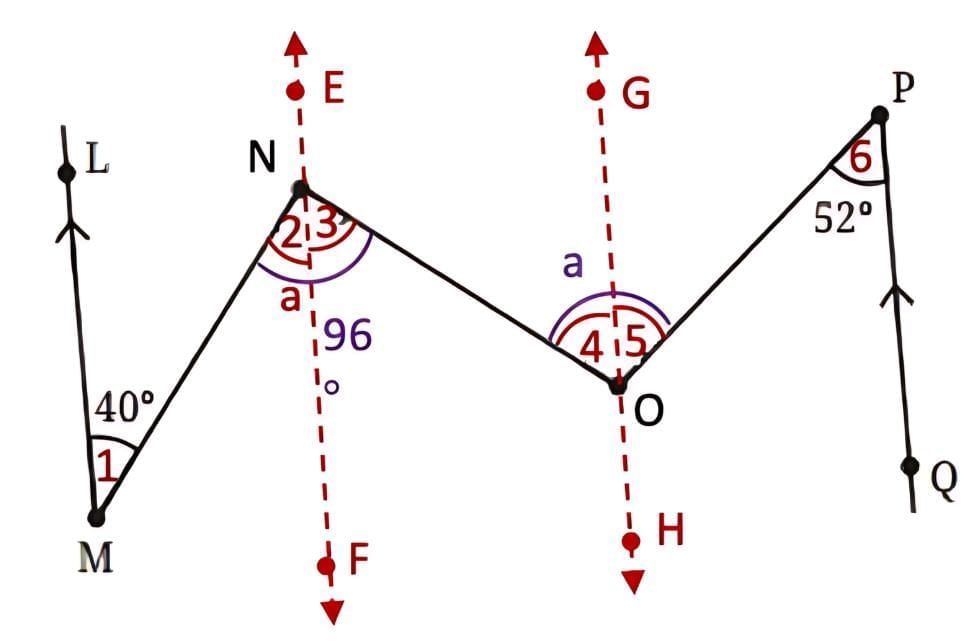 Construction: Draw lines EF and GH parallel to lines LM and PQ.
Construction: Draw lines EF and GH parallel to lines LM and PQ.
LM is parallel to EF and MN is a transversal, then
∠1 = ∠2 = 40°…….. (Alternate interior angles)
∠2 + ∠3 = 96°
40° + ∠3 = 96°
∠3 = 96° – 40°
∠3 = 56°.
EF is parallel to GH and NO is a transversal, then
∠3 = ∠4 = 56°…….. (Alternate interior angles)
Also, GH is parallel to PQ and OP is a transversal, then
∠5 = ∠6 = 52°…….. (Alternate interior angles)
a = ∠4 + ∠5
a = 56° + 52°
a = 108°.
Parallel Illusions
Q: There do not seem to be any parallel lines here. Or, are there? 
What causes these illusions?
Ans: (a) At first glance, the image looks chaotic, with lines appearing tilted or uneven. However, the vertical lines are actually straight, evenly spaced, and parallel. The diagonal lines, fanning out like spokes, intersect the vertical ones, creating an optical illusion. This illusion tricks our brain into perceiving distortion because the slanted lines and central focal point mislead our sense of alignment.
(b) This pattern seems filled with zigzagging lines and tilted shapes, making it appear uneven. But the white horizontal spaces between the black shapes are truly parallel. The illusion occurs because the bold, slanted black shapes distort our visual perception, making the white lines seem slanted or uneven.
(c) Though the image seems curved and pulled inward, the top and bottom horizontal lines are actually parallel. The radiating diagonal lines from the center create a depth illusion, making the straight lines appear bent. This classic optical illusion deceives our brain into seeing curves where none exist.
|
41 videos|251 docs|8 tests
|
FAQs on NCERT Solutions for Class 7 Maths Chapter 5 Parallel and Intersecting Lines
| 1. What are parallel lines? |  |
| 2. How can you identify intersecting lines? |  |
| 3. What is the difference between parallel and intersecting lines? |  |
| 4. Can two lines be both parallel and intersecting? |  |
| 5. How do you construct parallel lines using a ruler and compass? |  |
















