NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals - 1 (Exercise 3.1)
Exercise 3.1
Q1: Given here are some figures.
1.
2.
3.
4.
5.
6.
7.
8.
Classify each of them on the basis of the following
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Sol:
(a) Simple curves are: (1), (2), (5), (6) and (7).
A simple curve is a curve that does not cross itself.
(b) Simple closed curves are: (1), (2), (5), (6), and (7).
In simple closed curves the shapes are closed by line segments or by curved lines.
(c) Polygons are: (1), (2)
A simple closed curve made up of only line segments is called a polygon.
(d) Convex polygon is: (2)
A Convex polygon is defined as a polygon with no portions of its diagonals in its exteriors.
(e) Concave polygon is: (1)
A concave polygon is defined as a polygon with one or more interior angles greater than 180°.
Note
'4' is not a polygon because polygon is a simple closed curve made up of line segments and the 4th figure is not a simple curve because it crosses itself. Therefore, '4' is not a polygon. In the latest edition, this figure is no longer listed as the polygon.
Q2: What is a regular polygon? State the name of a regular polygon of the following sides
(a) 3 sides (b) 4 sides (c) 6 sides
Ans: A polygon is said to be a regular polygon if:
- The measures of its interior angles are equal and
- The lengths of its sides are equal
(a) A regular polygon of three sides is called an equilateral Triangle.
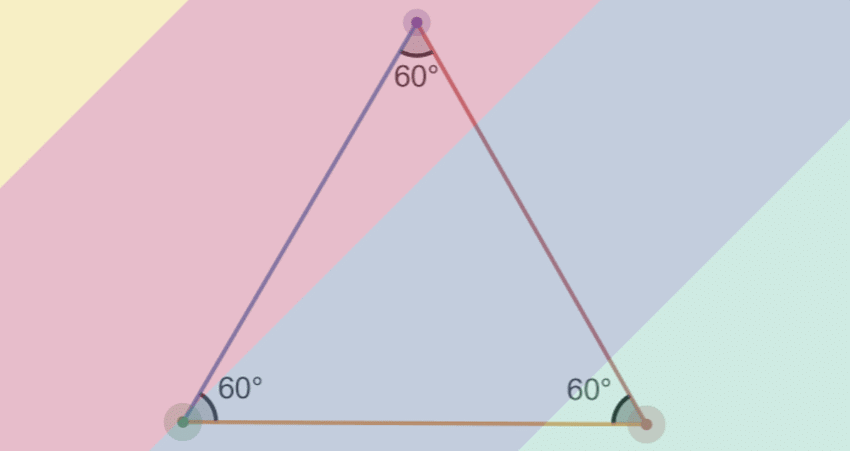 An Equilateral Triangle
An Equilateral Triangle
(b) A regular polygon of 4 sides is called a square.
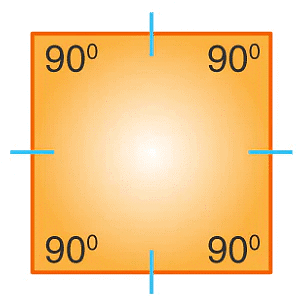 A square(c) A regular polygon of 6 sides is called a regular hexagon.
A square(c) A regular polygon of 6 sides is called a regular hexagon.
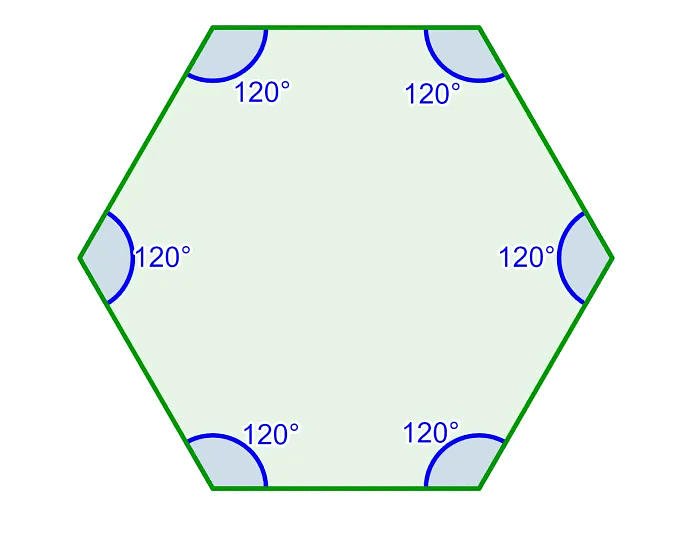 A regular polygon
A regular polygon
Exercise 3.2
Q1: Find x in the following figures.
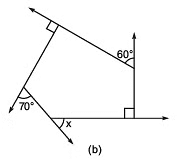
Sol:
(a)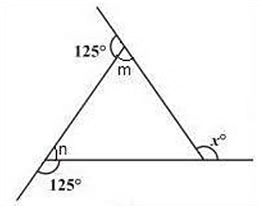
125° + m = 180°
⇒ m = 180° – 125° = 55° (Linear pair)
125° + n = 180°
⇒ n = 180° – 125° = 55° (Linear pair)
x = m + n (The exterior angle of a triangle is equal to the sum of the two opposite interior angles)
⇒ x = 55° + 55° = 110°
(b)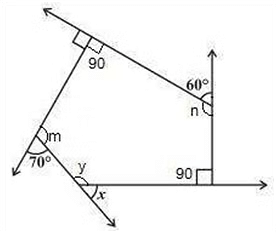 Two interior angles are right angles = 90°
Two interior angles are right angles = 90°
70° + m = 180°
⇒ m = 180° – 70° = 110° (Linear pair)
60° + n = 180°
⇒ n = 180° – 60° = 120° (Linear pair) The figure is having five sides and is a pentagon.
Sum of interior angles of a polygon = (n-2) * 180°
Thus, sum of the angles of a pentagon = (5-2)*180° = 540°
⇒ 90° + 90° + 110° + 120° + y = 540°
⇒ 410° + y = 540°
⇒ y = 540° – 410° = 130°
x + y = 180° (Linear pair)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
Q2: Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
Ans: Number of sides (n) = 9
∴ Number of exterior angles = 9
Since, sum of all the exterior angles = 360°
∵ The given polygon is a regular polygon.
∴ All the exterior angles are equal.
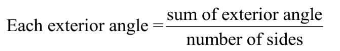
∴ Measure of an exterior angle = 360°/9° = 40°
(ii) 15 sides
Ans: Number sides of regular polygon = 15
∴ Number of equal exterior angles = 15
∵ The sum of all the exterior angles = 360°
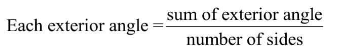
∴ The measure of each exterior angle = 360°/15 = 24°
Q3: How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Sol: Each exterior angle = sum of exterior angles/Number of angles
24°= 360/ Number of sides
⇒ Number of sides = 360/24 = 15
Thus, the regular polygon has 15 sides.
Q4: How many sides does a regular polygon have if each of its interior angles is 165°?
Sol: The given polygon is regular polygon.
Each interior angle = 165°
∴ Each exterior angle = 180° – 165° = 15°
∴ Number of sides = 360°/15° = 24
Thus, there are 24 sides of the polygon.
Q5: (a) Is it possible to have a regular polygon with measure of each exterior angle is 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Sol: (a) Each exterior angle = 22°
∴ Number of sides = 360°/22° = 180/11
If it is a regular polygon, then its number of sides must be a whole number.
Here, 180/11 is not a whole number.
∴ 22° cannot be an exterior angle of a regular polygon.
(b) If 22° is an interior angle, then 180° – 22°, i.e. 158° is exterior angle.
∴ Number of sides = 360°/158° = 180°/79°
Which is not a whole number.
Thus, 22° cannot be an interior angle of a regular polygon.
Q6: (a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Sol: (a) The minimum number of sides of a polygon = 3
The regular polygon of 3-sides is an equilateral.
∵ Each interior angle of an equilateral triangle = 60°
Hence, the minimum possible interior angle of a polynomial = 60°
(b) ∵ The sum of an exterior angle and its corresponding interior angle is 180°.
The minimum interior angle of a regular polygon = 60°
∴ The maximum exterior angle of a regular polygon = 180° – 60° = 120°
Deleted Questions from NCERT
Q1: How many diagonals does each of the following have? (a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
Ans: A diagonal is a line segment connecting two non-consecutive vertices of a polygon. Draw the above-given polygon and mark vertices and then, draw lines joining the two non-consecutive vertices. From this, we can calculate the number of diagonals.
(a) Convex quadrilateral
A convex quadrilateral has two diagonals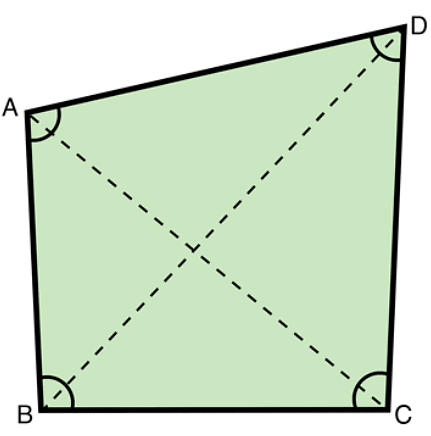
Here, AC and BD are two diagonals.
(b) Regular hexagon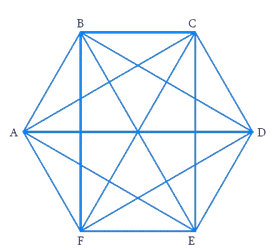
Here, the diagonals are AD, AE, BD, BE, FC, FB, AC, EC, and FD. There are 9 diagonals.
(c) A triangle
 All these are triangles
All these are triangles
A triangle has no diagonal because there are no two non-consecutive vertices.
Note: Number of diagonals in a polygon of n-sides =
Q2: What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Sol: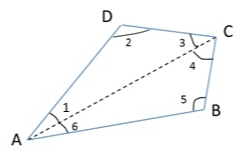
ABCD is a convex quadrilateral made of two triangles ΔABC and ΔADC. We know that the sum of the angles of a triangle is 180 degrees. So,
- ∠6+∠5+∠4 = 180° (Sum of the angles of ΔABC is 180°)
- ∠1+∠2+∠3 = 180° (Sum of the angles of ΔADC is 180°)
Adding the above equations, we get: - ∠6+∠5+∠4+∠1+∠2+∠3 = 360°
On Rearranging the terms:
- ∠6+∠1+∠3+∠4+∠5+∠2 = 360°
- ∠A+∠C+∠B+∠D = 360° (∠6+∠1 = ∠A, ∠3+∠4 = ∠C )
- Hence, the sum of measures of the triangles of a convex quadrilateral is 360∘.
Yes, even if the quadrilateral is not convex then, this property applies. Let ABCD be a non-convex quadrilateral; join BD, which also divides the quadrilateral into two triangles.
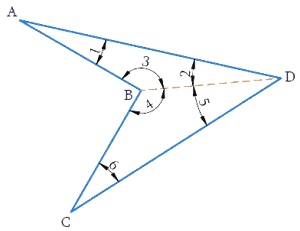
Using the angle sum property of triangle again, ABCD is a concave quadrilateral, made of two triangles ΔABD and ΔBCD. Therefore, the sum of all the interior angles of this quadrilateral will also be, 180∘+180∘ = 360∘
Q3: Find the angle measure x in the following figures.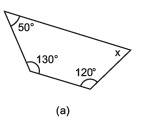
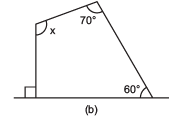
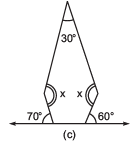
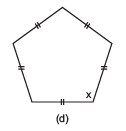
Sol:
(a) The figure is having four sides. Hence, it is a quadrilateral.
As the sum of interior angles of a quadrilateral = 360°
⇒ x + 120° + 130° + 50° = 360°
⇒ x + 300° = 360°
⇒ x = 360° – 300° = 60°
(b) The figure has four sides. Hence, it is a quadrilateral. Also, one side is perpendicular.
As, the sum of interior angles of a quadrilateral = 360°
The figure has four sides. Hence, it is a quadrilateral.
⇒ x + 60° + 70° + 90° = 360°
⇒ x + 220° = 360°
⇒ x = 360° – 220° = 140°
(c) The figure is having 5 sides. Hence, it is a pentagon.
Sum of interior angles of a pentagon = 540°
Two angles at the bottom are forming linear pair.
∴ 180° - 70° = 110°
180° – 60° = 120°
∴ Interior angles are 30°, x°, x°, 110°, and 120°
⇒ 30° + x + x + 110° + 120° = 540°
⇒ 2x + 260° = 540°
⇒ 2x = 280°
⇒ x = 140°
(d) The figure has 5 equal sides. Hence, It is a regular pentagon. Thus, it's all angles are equal.
Sum of all interior angles of a regular pentagon = 540°.
⇒ x + x + x + x + x = 540°
⇒ 5x = 540°
⇒ x = 540° ÷ 5 = 108°
Q4: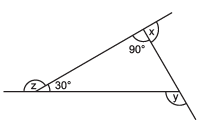

(a) Find x + y + z.
(b) Find x + y + z + w.
Sol: (a) Sum of all the angles of a triangle = 180°
∴ One angle of a triangle is 180° - (90°+30°) = 60°
⇒ x + 90° = 180° (Linear pair)
⇒ x = 180° – 90° = 90°
⇒ y = 30° + 90° = 120° (∵ Sum of interior opposite angles = exterior angle)
⇒ z = 180° – 30° = 150° (Linear pair)
Now, x + y + z = 90° + 120° + 150° = 360°
(b) Sum of interior angles of a quadrilateral = 360°
∴ ∠1 + 120° + 80° + 60° = 360°
⇒ ∠1 + 260° = 360°
⇒ ∠1 = 360° – 260° = 100°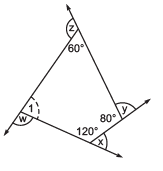 Now, x + 120° = 180° (Linear pair)
Now, x + 120° = 180° (Linear pair)
∴ x = 180° – 120° = 60°
y + 80° = 180° (Linear pair)
∴ y = 180° – 80° = 100°
z + 60 = 180° (Linear pair)
∴ z = 180° – 60° = 120°
w + 100 = 180° (Linear pair)
∴ w = 180° – 100° = 80°
Thus, x + y + z + w = 60° + 100° + 120° + 80° = 360°
Q5: Examine the table. (Each figure is divided into triangles and the sum of the angles is deduced from that).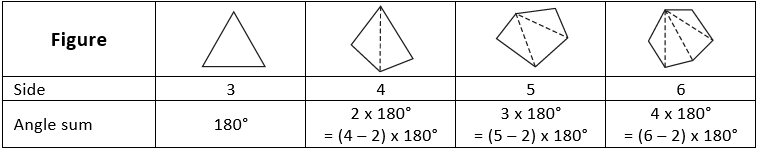
What can you say about the angle sum of a convex polygon with several sides?
(a) 7
(b) 8
(c) 10
(d) n
Sol: From the above table, we conclude that the sum of the interior angles of a polygon with n-sides = (n – 2) x 180°
(a) When n = 7
Substituting n = 7 in the above formula, we have:
Sum of interior angles of a polygon of 7 sides (i.e. when n = 7)
= (n – 2) x 180° = (7 – 2) x 180°
= 5 x 180° = 900°
(b) When n = 8
Substituting n = 8 in the above formula, we have:
Sum of interior angles of a polygon having 8 sides
= (n – 2) x 180° = (8 – 2) x 180°
= 6 x 180° = 1080°
(c) When n = 10
Substituting n = 10 in the above formula, we have:
Sum of interior angles of a polygon having 10 sides
= (n – 2) x 180°
= (10 – 2) x 180°
= 8 x 180° = 1440°
(d) When n = n
The sum of interior angles of a polygon having n-sides = (n – 2) x 180°.
|
94 videos|549 docs|42 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals - 1 (Exercise 3.1)
| 1. How many sides does a quadrilateral have? |  |
| 2. Can a quadrilateral have all sides of different lengths? |  |
| 3. What is the sum of the interior angles of a quadrilateral? |  |
| 4. How many diagonals does a quadrilateral have? |  |
| 5. Can a quadrilateral have only one pair of parallel sides? |  |

















