NCERT Solutions for Class 10 Maths - Polynomials Exercise 2.3
EXERCISE 2.3
Ques 1: Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :
(i) p(x) = x3 - 3x2 + 5x - 3, g(x) = x2 - 2
(ii) p(x) = x4 - 3x2 + 4x + 5, g(x) = x2 + 1 - x
(iii) p(x) = x4 - 5x + 6, g(x) = 2 - x2
Sol: Here, dividend p(x) = x3 - 3x2 + 5x - 3
divisor g(x) = x2 - 2
∴ We have
Thus, the quotient = (x - 3) and remainder = (7x - 9)
(ii) Here, dividend p(x) = x4 - 3x2 + 4x + 5
and divisor g(x) = x2 + 1 - x
= x2 - x + 1
∴ We have
Thus, the quotient is (x2 + x - 3) and remainder = 8
(iii) Here, dividend, p(x) = x4 - 5x + 6
and divisor, g(x) = 2 - x2
= - x2 + 2
∴ We have
Thus, the quotient = –x2 – 2 and remainder = –5x + 10.
Ques 2: Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial: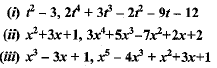
Sol. (i) Dividing 2t4 + 3t3 - 2t2 - 9t - 12 by t2 - 3, we have:
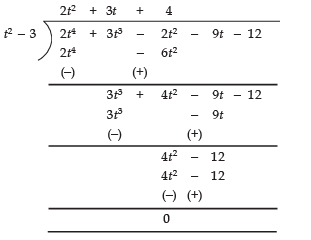
∵ Remainder = 0
∴ (t2 - 3) is a factor of 2t4 + 3t3 - 2t2 - 9t - 12.
(ii) Dividing 3x4 + 5x3 - 7x2 + 2x + 2 by x2 + 3x + 1, we have:
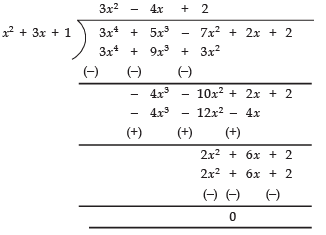
∵ Remainder = 0.
∴ x2 + 3x + 1 is a factor of 3x4 + 5x3 - 7x2 + 2x + 2.
(iii) Dividing x5 - 4x3 + x2 + 3x + 1 by x3 - 3x + 1, we get:
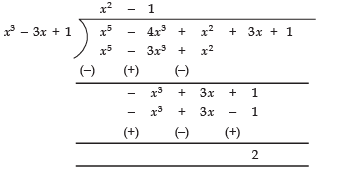
∴ The remainder = 2, i.e., remainder ≠ 0
∴ x3 - 3x + 1 is not a factor of x5 - 4x3 + x2 + 3x + 1.
Ques 3: Obtain all other zeroes of 3x4 + 6x3 - 2x2 - 10x - 5, if two of its zeroes are -
.
Sol: We have p(x) = 3x4 + 6x3 - 2x2 - 10x - 5
α = and β = -
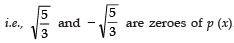
∴ is a factor of p (x).
Now, let us divide 3x4 + 6x3 - 2x2 - 10x - 5 by 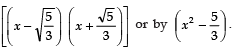 .
.
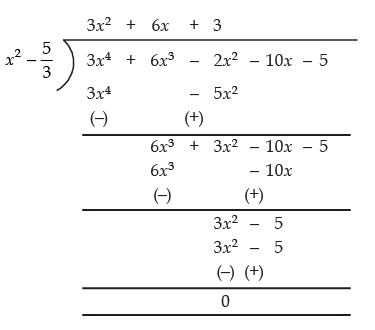
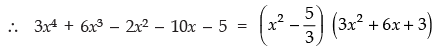
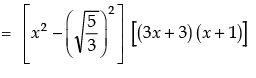
For p (x) = 0, we have
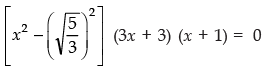
i.e., 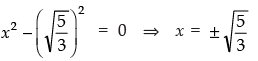
or 3x + 3 = 0 ⇒ x = - 1
or x + 1 = 0 ⇒ x = - 1
Thus, all the other zeroes of the given polynomial are - 1 and - 1.
Ques 4: On dividing x3 - 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x - 2 and -2x + 4 respectively. Find g(x).
Sol: Here,
Dividend p(x) = x3 - 3x2 + x + 2
Divisor = g(x)
Quotient = (x - 2)
Remainder = (-2x + 4)
Since,
(Quotient × Divisor) + Remainder = Dividend
∴ [(x − 2) × g(x)] + [(−2x + 4)] = x3 − 3x2 + x + 2
⇒ (x − 2) × g(x)= x3 − 3x2 + x + 2 − (−2x + 4)
= x3 − 3x2 + x + 2 + 2x −4
= x3 - 3x2 + 3x - 2
∴ 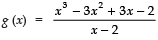
Now, dividing x3 - 3x2 + 3x - 2 by x - 2, we have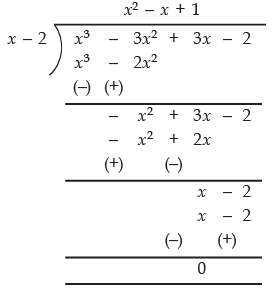
∴ 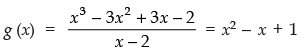
Thus, the required divisor g(x) = x2 - x + 1.
Ques 5: Give example of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Sol:
(i) p(x), g(x), q(x), r(x)
deg p(x) = deg q(x)
∴ both g(x) and r(x) are constant terms.
p(x) = 2x2- 2x + 14
g(x) = 2
q(x) = x2 - x + 7
r(x) = 0
(ii) deg q(x) = deg r(x)
∴ this is possible when deg of both q(x) and r(x) should be less than p(x) and g(x).
p(x) = x3 + x2 + x + 1
g(x) = x2 - 1
q(x) = x + 1, r(x) = 2x + 2
(iii) deg r(x) is 0.
This is possible when product of q(x) and g(x) form a polynomial whose degree is equal to degree of p(x) and constant term.
NOTE: We have given one example for each of the above cases, however, there can be several examples for them.
|
70 videos|242 docs|187 tests
|
FAQs on NCERT Solutions for Class 10 Maths - Polynomials Exercise 2.3
| 1. What is a polynomial? |  |
| 2. How do you identify the degree of a polynomial? |  |
| 3. What is the difference between a monomial and a binomial? |  |
| 4. How do you add or subtract polynomials? |  |
| 5. Can a polynomial have a negative degree? |  |






















