NCERT Solutions for Class 4 Maths Chapter 5 - Sharing and Measuring
Page 62: Let Us Discuss
Ikra and her little sister, Samina, decide to make a drawing, but they are left with a single drawing sheet. Ikra wants to share the paper by dividing it in half, but Samina insists on having a bigger part of the paper. Ikra thought for a moment and proposed a solution.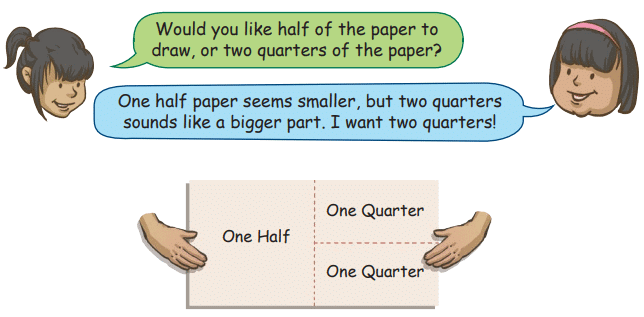
Q1: Which part of the paper would you have chosen—one half or two quarters? Why?
Ans: I would choose one half. One-half is the same as two quarters because two quarters 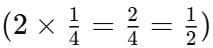 . Both are equal parts of the paper.
. Both are equal parts of the paper.
Q2: Do you think Ikra shared the paper equally? Why? Try with a paper.
Ans: Yes, Ikra shared the paper equally. One-half (1/2) is the same as two quarters (2/4). If you fold a paper in half or into four equal parts and take two parts, the size is the same.
Q3: How do you know that the paper has been divided equally?
Ans: The paper is divided equally if each part is the same size. For one half, fold the paper into two equal parts. For two quarters, fold it into four equal parts and take two. Both cover the same area.
Q4: Why do you think Samina chose two quarters of the paper?
Ans: Samina chose two quarters because she thought it sounded like a bigger part. She didn’t realize that two quarters (2/4) is the same as one half (1/2).
Page 63: Let Us Do
Q1: Samina has divided some figures into two parts. Colour the figures that are divided into halves correctly. How did you get the answer?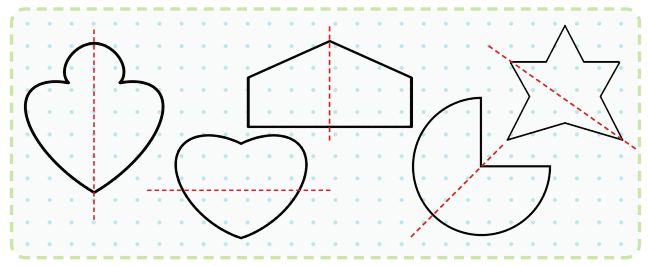
Ans: To find halves, each part must be equal in size. Check if the figure is divided into two equal parts. Colour only those figures where both parts are the same size. I got the answer by looking at the shapes and comparing the size of the two parts.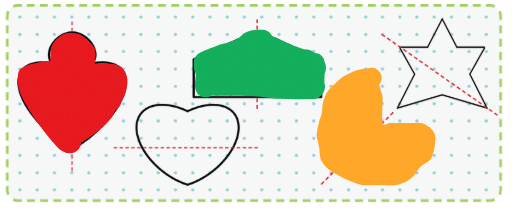
Q2: Divide the shapes into halves by drawing a line.
Ans: Draw a line through the middle of each shape so that both parts are equal in size. For example, for a rectangle, draw a vertical or horizontal line to split it into two equal parts.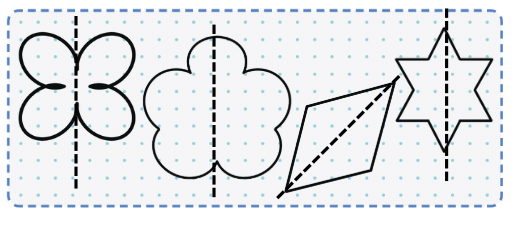
Page 64: Let Us Do
Q3: Divide these shapes into 4 equal parts/quarters.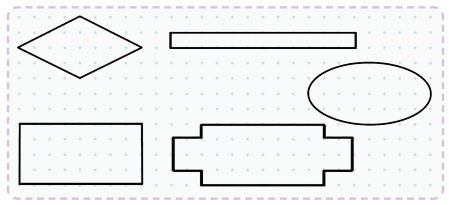
Ans: Draw lines to split each shape into four equal parts. For a rectangle, draw one vertical and one horizontal line to make four equal rectangles. For a circle, draw two lines through the center to make four equal sections.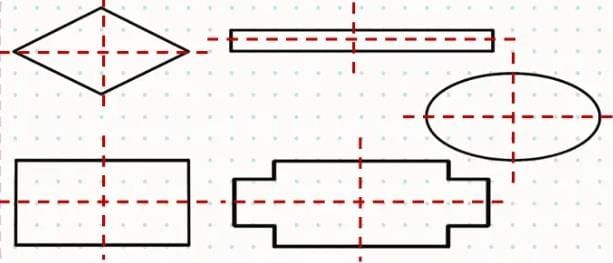
Page 64: Let Us Try
Q4: In how many different ways can you fold/cut a rectangular paper in two equal parts? Try it with a rectangular paper.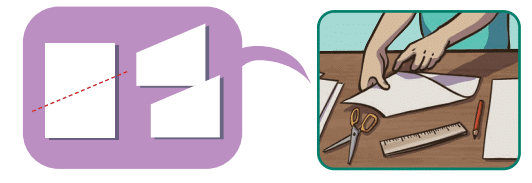
Ans: You can fold or cut a rectangular paper in two equal parts in these ways:
Fold vertically to make two equal rectangles.

Fold horizontally to make two equal rectangles.

Fold diagonally from one corner to the opposite corner to make two equal triangles.
There are at least three different ways.
Page 65: Let Us Do
Q2: Now try to draw and show five different ways in which we can fold/cut a rectangle into four equal parts (1/4 or quarter).
Ans: Five ways to fold or cut a rectangle into four equal parts:
Draw three vertical lines to make four equal vertical strips.
Draw three horizontal lines to make four equal horizontal strips.
Draw one vertical and one horizontal line to make four equal rectangles.
Draw two diagonal lines from opposite corners to make four equal triangles.
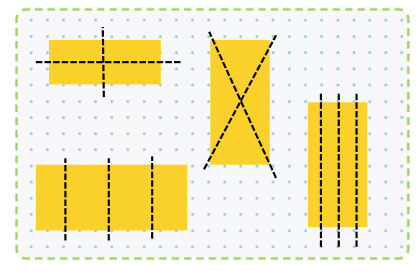
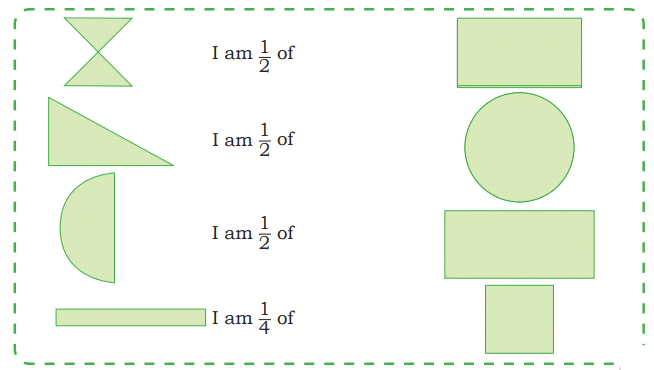
Q3: Match the following parts with their corresponding wholes.
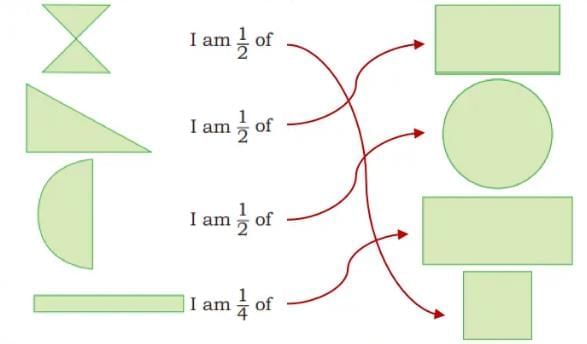
Ans:
Page 66 - 68 Ding Dong
Q. How much dhokla does Sumedha get now?
Ans: Each children get 1/5 part of dhokla
Sumedha's Part = 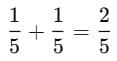
Page 68: Let Us Discuss
Q1: What is Sumedha observing about her share as each guest comes in?
Ans: Sumedha observes that her share of dhokla gets smaller as more guests come. When shared with more people, each person gets a smaller piece.
Q2: In which situation will Sumedha get to eat more dhokla: when shared among 9 people or 11 people?
Ans: Sumedha will get more dhokla when shared among 9 people. If the dhokla is divided into 9 parts, each piece is bigger than when divided into 11 parts.
Q3: How many pieces of 1/6 would make a complete dhokla?
Ans: Six pieces of 1/6 make a complete dhokla because .
.
Q4: What would be Sumedha’s share, if Idha and Vinayak both give their share of dhokla to her?
Ans: Idha’s share = 1/5
Vinayak’s share = 1/5
Sumedha’s total share =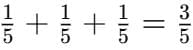
So, Sumedha will get 3/5 of the dhokla if both Idha and Vinayak give their share to her.
Page 68: Let Us Do
Q1: How much dhokla would each person get if it was shared equally among 6 people? Try also with 8 people. Who will get the bigger pieces of dhokla? Draw and explain.
Ans:
For 6 people: Divide the dhokla into 6 equal parts. Each person gets 1/6 of the dhokla.
For 8 people: Divide the dhokla into 8 equal parts. Each person gets 1/8 of the dhokla.
Explanation: The pieces are bigger when shared among 6 people because 1/6 is larger than 1/8. Draw a circle for the dhokla, divide it into 6 parts, and then into 8 parts to see that 1/6 is bigger.

Page 69: Let Us Do
Q2: Shade a portion of the dhokla to represent the fraction Sumedha would get when the dhokla is shared equally among the given number of people. Discuss why the fractions get smaller.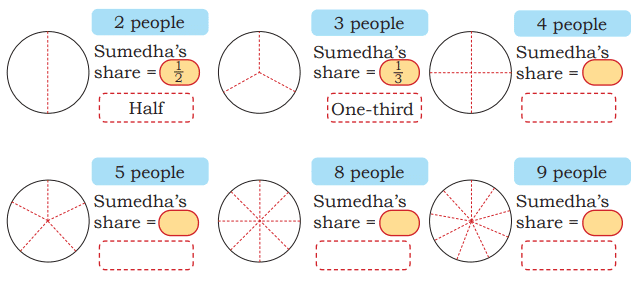
Ans: Divide the dhokla into equal parts based on the number of people and shade one part to show Sumedha’s share. For example, if 4 people, shade 1/4; if 5 people, shade 1/5. The fractions get smaller because as more people share the same dhokla, each person’s share becomes a smaller part of the whole.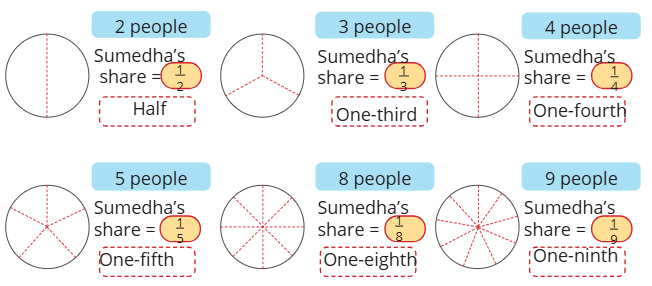
Page 69: Let Us Discuss
Q1: Share your observations about the different pieces and the whole.
Ans: The whole is the complete object, like a dhokla or paper. When divided into equal pieces, each piece is a fraction of the whole. For example, 1/2 is one of two equal parts, and 1/4 is one of four equal parts. Smaller fractions mean more pieces and smaller sizes.
Q2: Take any two different pieces of the fraction kit and compare them. Discuss which one is smaller and why.
Ans: Take two pieces, like 1/3 and 1/4.
Compare their sizes. 1/4 is smaller than 1/3 because the whole is divided into more parts (4 parts) for 1/4, so each part is smaller than when divided into 3 parts for 1/3.
Q3: Sumedha noticed that when a whole is equally divided into a larger number of parts, each part gets smaller. Do you agree with Sumedha?
Ans: Yes, I agree with Sumedha. When the whole is divided into more parts, each part is smaller. For example, 1/6 is smaller than 1/4 because 6 parts are smaller than 4 parts of the same whole.
Q4: Sumedha says, “When I join 5 pieces of 1/5, it makes a whole dhokla.” Try to do it yourself with your fraction kit. Ans: Yes, Sumedha is correct. Take 5 pieces of 1/5 from the fraction kit.
Ans: Yes, Sumedha is correct. Take 5 pieces of 1/5 from the fraction kit.
When you join them, they make a whole dhokla because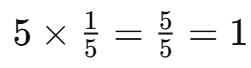
Q5: Sumedha says that this part is one-third of the complete whole. Why is she saying so?
Ans: Sumedha says it is one-third because the whole is divided into three equal parts, and one part is shaded or taken. One-third (1/3) means one out of three equal parts of the whole.
Page 70: Let Us Try
Q1: ______ is greater than _________. (1/5, 1/4).
Ans: 1/4 is greater than 1/5.
When the whole is divided into 4 parts, each part (1/4) is bigger than when divided into 5 parts (1/5).
Q2: ________ > __________. (1/9, 1/6).
Ans: 1/6 is greater than 1/9.
When the whole is divided into 6 parts, each part (1/6) is bigger than when divided into 9 parts (1/9).
Q3: 1/6 _______ 1/8.
Ans: 1/6 is greater than 1/8.
Same as above, 1/6 is larger because fewer parts mean bigger pieces.
Q4: ______ is smaller than _______ ( ______, _______).
Ans: 1/7 is smaller than 1/5.
Page 70: My Flower Garden
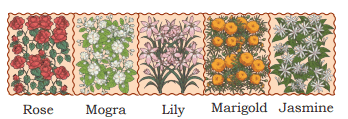
Mogra in 1/5 or one-fifth part of the garden.
Marigold in _______ part of the garden.
Jasmine in _______ part of the garden.
Rose in 1/5 and 1/5 or a total of 2/5 (two-fifths) part of the garden.
Ans:
Marigold in 1/5 part of the garden.
Jasmine in 1/5 part of the garden.
Page 71: Look at the garden and Answer the questions.

Mogra in _____ part
Marigold in _____ part
Rose in 1/5 + 1/5 + 1/5 part or a total of 3/5 (three-fifths) part
Ans:
Mogra: 1/5 (one of the remaining parts)
Marigold: 1/5 (one of the remaining parts)
Look at the garden and answer the questions.

a) Marigold in ...........
Ans: The garden is divided into 5 equal parts (1/5 each).
Marigold: 1/5
b) Rose: 4/5 (given as 1/5 + 1/5 + 1/5 + 1/5 = 4/5): True

Page 71: Let Us Do
Make a flower garden with seven flowering seeds—Mogra, Marigold, Jasmine, Rose, Lily, Hibiscus, and Periwinkle?


Ans: 


Page 73: Do It Yourself
Write the fractions for each of the toppings in the following dosas.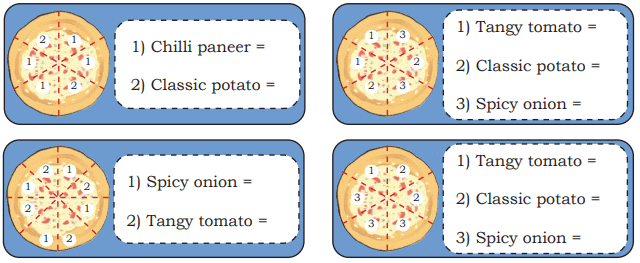
Ans: 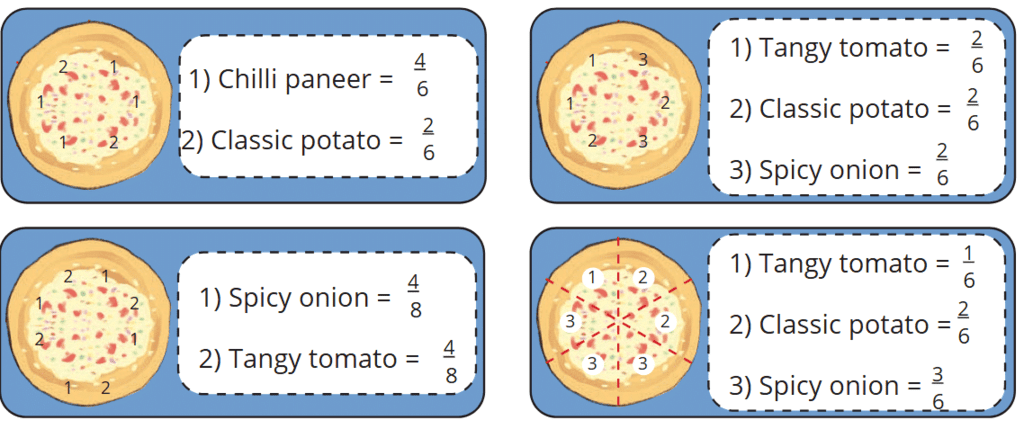
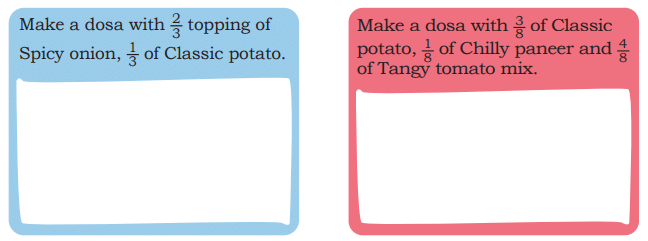
Make a dosa with 2/3 topping of Spicy onion, 1/3 of Classic potato.
Ans: Divide the dosa into 3 equal parts. Shade 2 parts for Spicy onion (2/3) and 1 part for Classic potato (1/3).
Make a dosa with 2/3 of Classic potato, 1/8 of Chilly paneer and 4/5 of Tangy tomato mix.
Ans: This seems incorrect as 2/3 + 1/8 + 4/5 exceeds 1. Assuming a typo, a possible correction is: Divide the dosa into 24 equal parts (LCM of 3, 8, 5). Shade 16/24 for Classic potato (2/3), 3/24 for Chilly paneer (1/8), and 19/24 for Tangy tomato (≈4/5, adjusted).
Page 73: Let Us Explore
Meena has 8 diyas. Colour 1/4 of her diyas red. To find 1/4, let us divide the number of diyas into 4 equal parts. Can you see how to divide the diyas into 4 equal parts? Now colour 2 diyas red.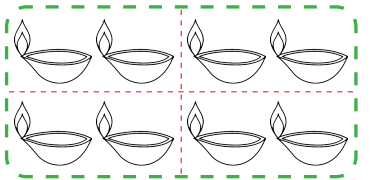
Ans: Divide 8 diyas into 4 equal parts: 8 ÷ 4 = 2 diyas per part. One-fourth (1/4) of 8 is 2 diyas. Colour 2 diyas red.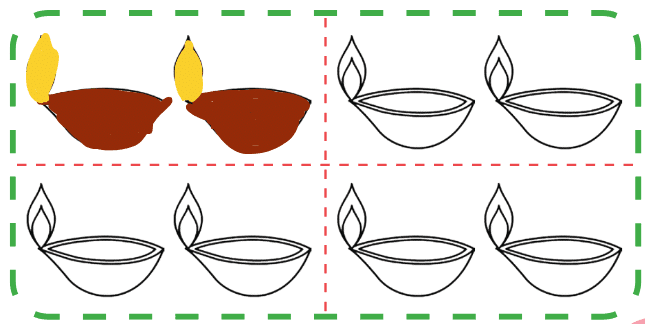
Page 74: Let Us Do
Now let us try to find fractions for the situations given below. Circle the appropriate parts in the pictures.
Q1: There are 12 cookies. What fraction of cookies will each get if the number of children are as follows:
a) 3 children
Ans: 12 ÷ 3 = 4 cookies each.
Fraction: 4/12 = 1/3. b) 6 children
b) 6 children
Ans: 12 ÷ 6 = 2 cookies each.
Fraction: 2/12 = 1/6. c) 2 children
c) 2 children
Ans: 12 ÷ 2 = 6 cookies each.
Fraction: 6/12 = 1/2. d) 4 children
d) 4 children
Ans: 12 ÷ 4 = 3 cookies each.
Fraction: 3/12 = 1/4.
Q2: Simran calls her school friends for her birthday party. 1/3 of her friends receive a hairband as their return gift. Place hairbands on 1/3 of her friends.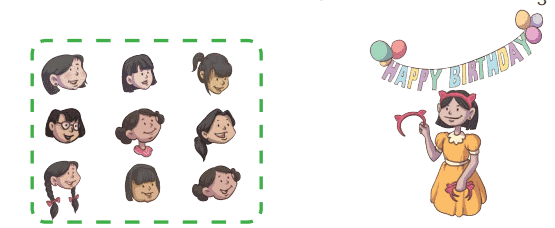
Ans: Count the number of friends. Divide by 3 to find 1/3. Place hairbands on that many friends. For example, if 9 friends, 1/3 = 3 friends get hairbands.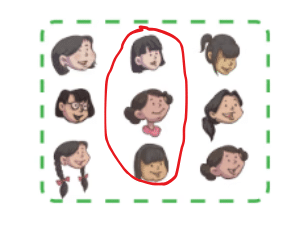
Q3: Draw flowers in 1/5 of the given number of pots.
Ans: Count the number of pots. Divide by 5 to find 1/5. Draw flowers in that many pots. For example, if 15 pots, 1/5 = 3 pots with flowers.
Page 75: Let Us Find Fractions in Our Surroundings
Q1: Yesterday, Mummy asked to divide a box of barfis into four equal parts. There are 16 barfis in the box. Draw a picture of 16 barfis and find 1/4 of the whole. How many barfis are in each part?
Ans: Draw 16 barfis in a 4x4 grid. Divide into 4 equal parts: 16 ÷ 4 = 4 barfis per part. One-fourth (1/4) is 4 barfis.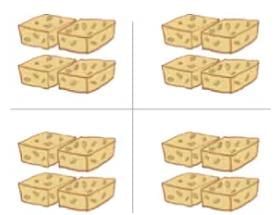
Q2: Rohan has a piece of ribbon to decorate his notebook. Mohan’s ribbon is one-fourth as long as Rohan’s ribbon. How long will Rohan’s ribbon be? Draw it. 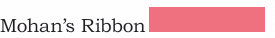
Ans: If Mohan’s ribbon is 1/4 of Rohan’s, Rohan’s ribbon is 4 times Mohan’s. Draw Rohan’s ribbon 4 times longer than Mohan’s. For example, if Mohan’s is 1 cm, Rohan’s is 4 cm.
Page 75: Try Yourself
Q. Observe your surroundings and think of situations where we use fractions, and write any two of them in the space provided below.
Ans:
Dividing a pizza into 8 equal slices, each slice is 1/8.
Sharing 12 chocolates among 4 friends, each gets 3/12 = 1/4.
Page 76: Let Us Do
1. Take a rectangular piece of paper and fold the paper into three equal parts and then unfold it.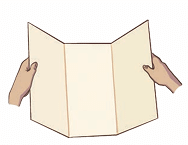
2. Colour one of the three equal parts as shown in the image.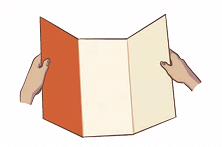
3. Fold the paper back into three equal parts like before, and then fold it in half.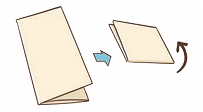
4. Observe the colored part. What is the fraction for the shaded part now? What does this mean?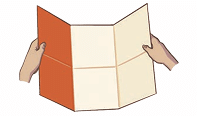
5. Fold the paper again and check how the coloured part changes.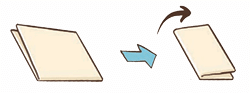
6. Write down what fraction you observe after each fold.
1/3 = 2/6 = ______ = ______ =______
Ans: 1/3 = 2/6 = 3/9 = 4/12 = 5/15
Page 77: Let Us Try
Q. Take another piece of paper and try the same starting with two equal parts, and halving every time. Share the findings with your friends.
Ans: Take a piece of paper. Fold it in half to make 2 equal parts. Fold it in half again to make 4 equal parts. Keep folding in half each time. You get 8 parts, then 16 parts, then 32 parts. Each fold makes twice as many parts as before.
1/2 = 2/4 = 4/8 = 8/16 = 16/32
Page 77: Let Us Discuss
Observe the fraction chart and discuss the following questions. 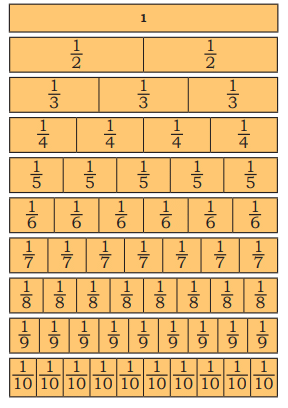
Q1: How many 1/4 s are equal to 1/2?
Ans: Two 1/4s equal 1/2 because 1/4 + 1/4 = 2/4 = 1/2, then answer is 2.
Q2: Is 2/3 less than or greater than 1/2?
Ans: 2/3 is greater than 1/2.
Compare: 2/3 = 4/6, 1/2 = 3/6.
Since 4/6 > 3/6, 2/3 is greater.
Q3: Ten pieces of 1/10 make a complete whole. Is this statement true?
Ans: Yes, true. Ten pieces of 1/10 make 10/10 = 1 whole.
Q4: Three pieces of 1/6 are equal to two pieces of 1/8. Is this true?
Ans: No, not true.
Three pieces of 1/6 = 3/6 = 1/2.
Two pieces of 1/8 = 2/8 = 1/4.
Since 1/2 ≠ 1/4.
Q5: How many pieces of 1/8 make 1/4?
Ans: Two pieces of 1/8 make 1/4 because 1/8 + 1/8 = 2/8 = 1/4.
Q6: Find the pieces that you can put together to make another bigger piece.
Ans: Do it Yourself!
Page 78: Let Us Do
Q1: Bablu is playing with square shapes. He wants to cut them in such a way that each piece is equal in size. Circle the squares that have been cut into equal parts. Write the fraction for the shaded part, whenever possible.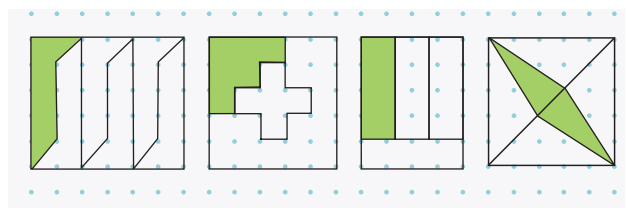
Ans: Circle the squares where each piece is the same size. For example, if a square is divided into four equal parts and one is shaded, the fraction is 1/4. If it’s not equal, don’t circle it.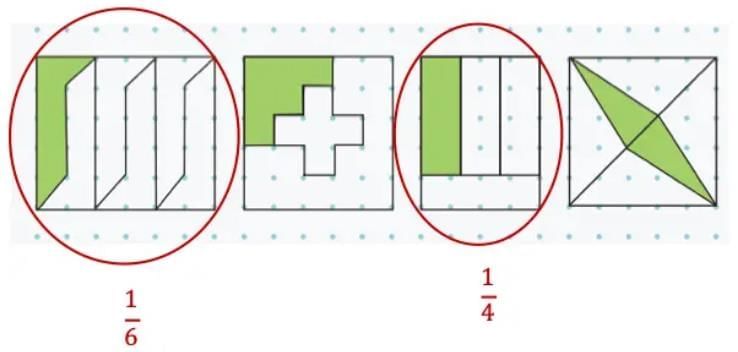
Q2: Check if the children’s claim below about the shaded parts of each of the pictures is correct. Circle the ones which you think are correct, cross out the ones which are not correct. You can draw additional lines to make the parts equal. Discuss your thinking.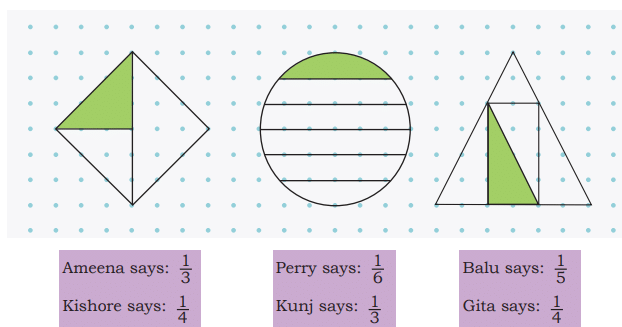
Ans: Do it Yourself!
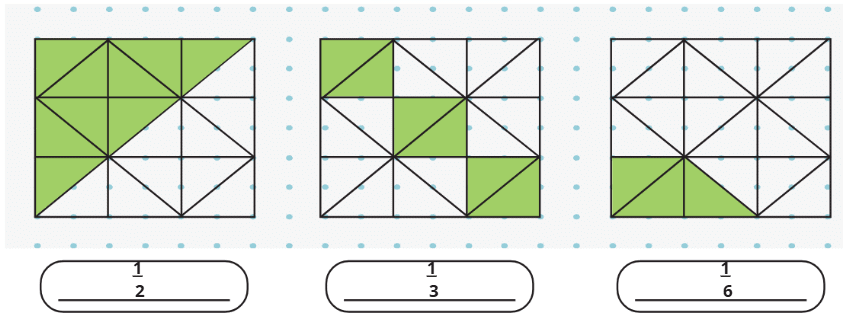
Q3: Identify the fractions represented by the coloured parts in the given pictures.
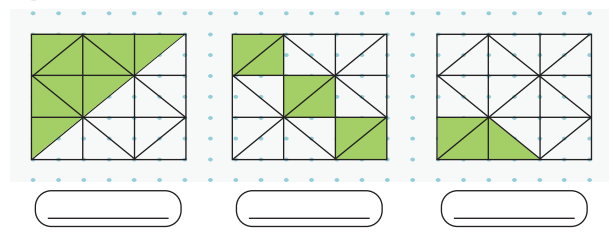
Q4: Identify the fraction of the whole that the blue parts make in each of the pictures given below.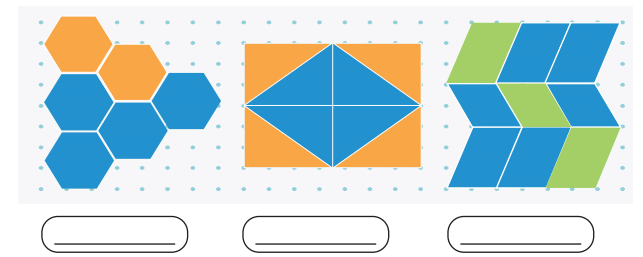
Ans: Count the total parts and the blue parts. For example, if 3 out of 4 parts are blue, the fraction is 3/4.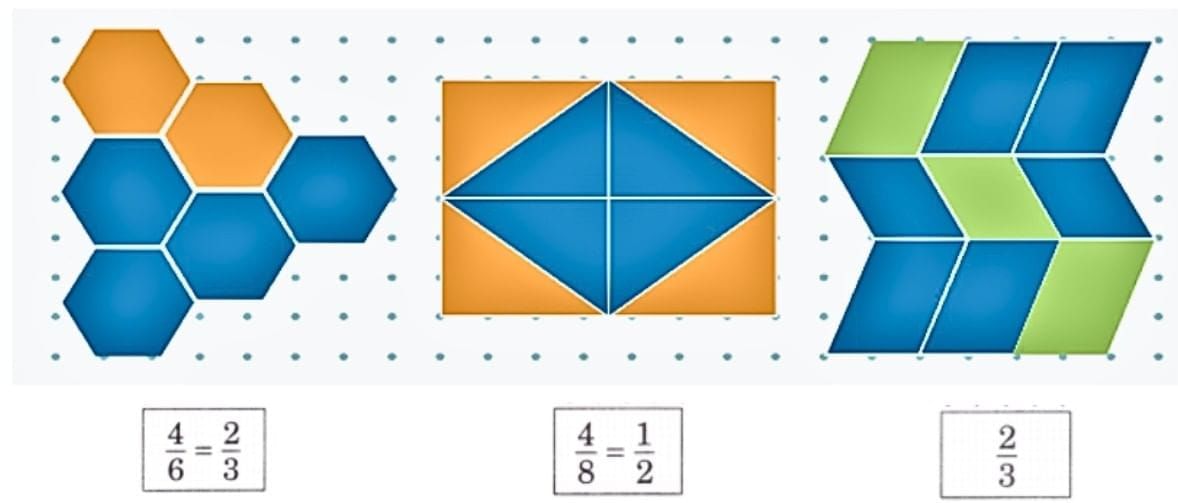
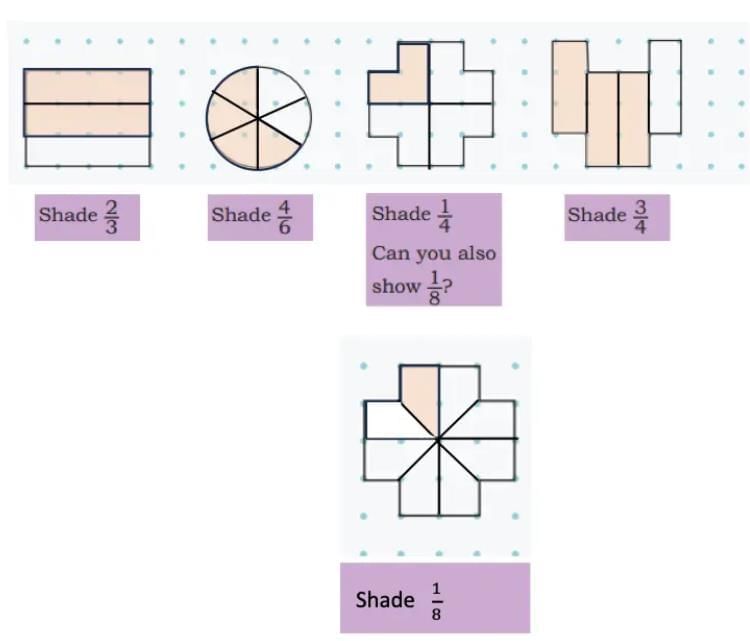
Q5: Divide the following into equal parts and shade the appropriate parts in each.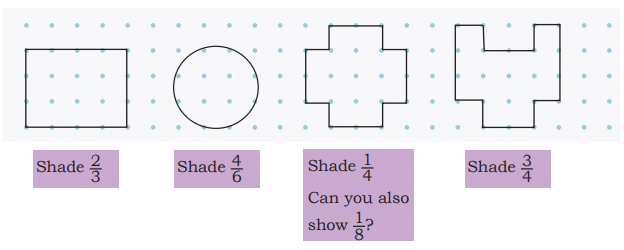
Ans:
Shade 2/3: Divide into 3 equal parts, shade 2.
Shade 4/6: Divide into 6 equal parts, shade 4.
Shade 1/4: Divide into 4 equal parts, shade 1.
Shade 3/4: Divide into 4 equal parts, shade 3.
|
54 videos|186 docs|14 tests
|
FAQs on NCERT Solutions for Class 4 Maths Chapter 5 - Sharing and Measuring
| 1. What is the main theme of the article "Let Us Discuss" and "Let Us Do"? |  |
| 2. How can students effectively participate in the activities mentioned in the article? |  |
| 3. What are some examples of activities that could be included under "Let Us Do"? |  |
| 4. Why is it important for students to try different approaches as suggested in "Let Us Try"? |  |
| 5. How can teachers facilitate discussions and activities effectively based on the article's content? |  |






















