The Solid State - 2 (Old NCERT) NCERT Solutions | Chemistry for JEE Main & Advanced PDF Download
Exercise Questions
Q1.1. Define the term ‘amorphous’. Give a few examples of amorphous solids.
Ans: Amorphous solids are solids without a regular/ definitive arrangement of its constituent particles (ions, atoms or molecules) and they possess something called the short-range order i.e., a regular and periodically repeating arrangement is seen only over short distances, e.g., rubber, glass.
Q1.2. What makes a glass different from a solid such as quartz? Under what conditions could quartz be converted into glass?
Ans: The arrangement of the constituent particles differentiates glass from quartz. The constituent particles in glass have a short-range order, but the constituent particles of quartz possess long range orders.
Quartz is converted into glass by heating it and then rapidly cooling it.
Q.1.3. Classify each of the following solids as ionic, metallic, molecular, network (covalent) or amorphous.
(i) Tetraphosphorus decoxide (P4O10)
(ii) Ammonium phosphate (NH4)3PO4
(iii) SiC
(iv) I2
(v) P4
(vi) Graphite
(vii) Brass
(viii) Rb
(ix) LiBr
(x) Si
Ans:
- Ionic:
(ii) Ammonium phosphate (NH4)3PO4
(x) LiBr - Metallic:
(viii) Brass
(ix) Rb - Molecular:
(i) Tetraphosphorus decoxide (P4O10)
(iv) I2
(v) P4 - Covalent (network):
(iii) SiC
(vii) Graphite
(xi) Si - Amorphous: (vi) Plastic
Q.1.4. (i) What is meant by the term 'Coordination number'?
(ii) What is the coordination number of atoms:
(a) in a cubic close-packed structure?
(b) in a body-centred cubic structure?
Ans:
(i) The number of nearest neighbours of any constituent particle present in the crystal lattice is called its coordination number.
(ii) The coordination number of atoms:
(a) in a cubic close-packed structure is 12, and
(b) in a body-centred cubic structure is 8
Q.1.5. How can you determine the atomic mass of an unknown metal if you know its density and the dimension of its unit cell? Explain.
Ans:
- By knowing the density of an unknown metal and the dimension of its unit cell, the atomic mass of the metal can be determined.
- Let ‘a’ be the edge length of a unit cell of a crystal, ‘d’ be the density of the metal, ‘m’ be the atomic mass of the metal and ‘z’ be the number of atoms in the unit cell.
Now, density of the unit cell
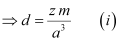
[Since the mass of the unit cell = Number of atoms in the unit cell × Atomic mass]
[Volume of the unit cell = (Edge length of the cubic unit cell)3]
From equation (i), we have: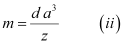
Now, mass of the metal (m) 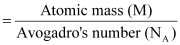
Therefore,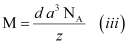
If the edge lengths are different (say a, b and c), then equation (ii) becomes:
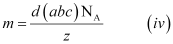
From equations (iii) and (iv), we can determine the atomic mass of the unknown metal.
Q.1.6. 'Stability of a crystal is reflected in the magnitude of its melting point'. Comment. Collect melting points of solid water, ethyl alcohol, diethyl ether and methane from a data book. What can you say about the intermolecular forces between these molecules?
Ans:
Higher the melting point, greater is the intermolecular force of attraction and greater is the stability. A substance with higher melting point is more stable than a substance with a lower melting point.
The melting points of the given substances are:
Solid water → 273 K
Ethyl alcohol → 158.8 K
Diethyl ether → 156.85 K
Methane → 89.34 K
Now, on observing the values of the melting points, it can be said that among the given substances, the intermolecular force in solid water is the strongest and that in methane is the weakest.
Q.1.7. Classify each of the following as being either a p-type or an n-type semiconductor:
(i) Ge doped with In
(ii) B doped with Si.
Ans:
(i) Ge (a group 14 element) is doped with In (a group 13 element). Therefore, a hole will be created and the semiconductor generated will be a p-type semiconductor.
(ii) B (a group 13 element) is doped with Si (a group 14 element). So, there will be an extra electron and the semiconductor generated will be an p-type semiconductor.
Q.1.8. How many lattice points are there in one unit cell of each of the following lattice?
(i) Face-centred cubic
(ii) Face-centred tetragonal
(iii) Body-centred
Ans:
(i) There are 14 (8 from the corners + 6 from the faces) lattice points in face-centred cubic.
(ii) There are 14 (8 from the corners + 6 from the faces) lattice points in face-centred tetragonal.
(iii) There are 9 (1 from the centre + 8 from the corners) lattice points in body-centred cubic.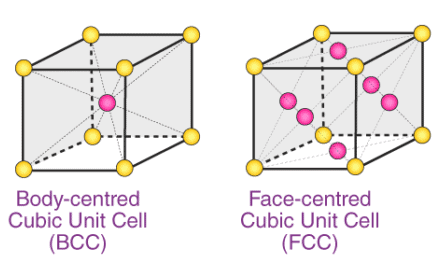
Q.1.9. Explain
(i) The basis of similarities and differences between metallic and ionic crystals.
(ii) Ionic solids are hard and brittle.
Ans:
(i) The basis of similarities between metallic and ionic crystals is that both these crystal types are held by the electrostatic force of attraction.
- In metallic crystals, the electrostatic force acts between the positive ions and the electrons.
- In ionic crystals, it acts between the oppositely charged ions. Hence, both have high melting points.
- The basis of differences between metallic and ionic crystals is that in metallic crystals, the electrons are free to move and so, metallic crystals can conduct electricity.
- However, in ionic crystals, the ions are not free to move. As a result, they cannot conduct electricity. However, in molten state or in aqueous solution, they do conduct electricity.
(ii) The constituent particles of ionic crystals are ions. These ions are held together in three-dimensional arrangements by the electrostatic force of attraction. Since the electrostatic force of attraction is very strong, the charged ions are held in fixed positions. This is the reason why ionic crystals are hard and brittle.
Q.1.10. If NaCl is doped with 10−3 mol % of SrCl2, what is the concentration of cation vacancies?
Ans:
- It is given that NaCl is doped with 10−3 mol% of SrCl2.
- This means that 100 mol of NaCl is doped with 10−3 mol of SrCl2.
- Therefore, 1 mol of NaCl is doped with mol of SrCl2 = 10−5 mol of SrCl2
- Cation vacancies produced by one Sr2+ ion = 1
- Hence, the concentration of cation vacancies created by SrCl2 is 6.022 × 108 per mol of NaCl.
Q.1.11. Silver crystallizes in fcc lattice. If edge length of the cell is 4.07 × 10−8 cm and density is 10.5 g cm−3, calculate the atomic mass of silver.
Ans: It is given that the edge length, a = 4.077 × 10−8 cm
Density, d = 10.5 g cm−3
As the lattice is fcc type, the number of atoms per unit cell, z = 4
We also know that NA = 6.022 × 1023 mol−1
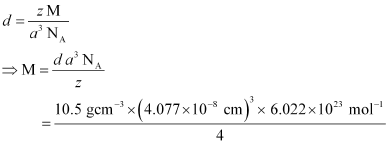
Using the relation:
= 107.13 gmol−1
Therefore, atomic mass of silver = 107.13 u
Q.1.12. A cubic solid is made of two elements P and Q. Atoms of Q are at the corners of the cube and P at the body centre. What is the formula of the compound? What are the coordination numbers of P and Q?
Ans: It is given that the atoms of Q are present at the corners of the cube.
Therefore, number of atoms of Q in one unit cell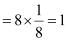
It is also given that the atoms of P are present at the body centre.
Therefore, number of atoms of P in one unit cell = 1
This means that the ratio of the number of P atoms to the number of Q atoms, P:Q = 1:1
Hence, the formula of the compound is PQ.
The coordination number of both P and Q is 8.
Q.1.13. Niobium crystallizes in a body-centred cubic structure. If density is 8.55 g cm−3, calculate atomic radius of niobium using its atomic mass 93 u.
Ans: It is given that the density of niobium, d = 8.55 g cm−3
Atomic mass, M = 93 gmol−1
As the lattice is bcc type, the number of atoms per unit cell, z = 2
We also know that, NA = 6.022 × 1023 mol−1
Applying the relation:

= 3.612 × 10−23 cm3
So, a = 3.306 × 10−8 cm
For body-centred cubic unit cell:
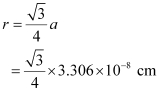
= 1.432 × 10−8 cm
= 14.32 × 10−9 cm
= 14.32 nm
Q.1.14. If the radius of the octahedral void is r and radius of the atoms in close packing is R, derive relation between r and R.
Ans:
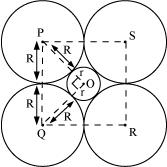
A sphere with centre O, is fitted into the octahedral void as shown in the above figure. It can be observed from the figure that ΔPOQ is right-angled
∠POQ = 900
Now, applying Pythagoras theorem, we can write:
PQ2 = PO2 + OQ2
⇒ (2R)2 = (R +r)2 + (R+r)2
⇒ (2R)2 = 2 (R + r)2
⇒ √2R = R+ r
⇒ r = √2R - R
⇒ r = (√2 - 1)R
⇒ r = 0.414 R
Q.1.15. Copper crystallises into a fcc lattice with edge length 3.61 × 10−8 cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm−3.
Ans: Edge length, a = 3.61 × 10−8 cm
As the lattice is fcc type, the number of atoms per unit cell, z = 4
Atomic mass, M = 63.5 g mol−1
We also know that, NA = 6.022 × 1023 mol−1
Applying the relation:
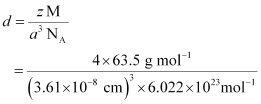
= 8.97 g cm−3
The measured value of density is given as 8.92 g cm−3. Hence, the calculated density 8.97 g cm−3 is in agreement with its measured value.
Q.1.16. Aluminium crystallises in a cubic close-packed structure. Its metallic radius is 125 pm.
(i) What is the length of the side of the unit cell?
(ii) How many unit cells are there in 1.00 cm3 of aluminium?
Ans:
(i) For cubic close-packed structure:
a = 2√2r
= 2√2 x 125 pm
= 353.55 pm
= 354 pm (approximately)
(ii) Volume of one unit cell = (354 pm)3
= 4.4 × 107 pm3
= 4.4 × 107 × 10−30 cm3
= 4.4 × 10−23 cm3
Therefore, number of unit cells in 1.00 cm3 = 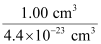
= 2.27 × 1022
Q.1.17. Gold (atomic radius = 0.144 nm) crystallises in a face-centred unit cell. What is the length of a side of the cell?
Ans: For a face-centred unit cell:
a = 2√2r
It is given that the atomic radius, r = 0.144 nm
So, 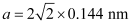
= 0.407 nm
Hence, length of a side of the cell = 0.407 nm
Q.1.18. In terms of band theory, what is the difference
(i) Between a conductor and an insulator
(ii) Between a conductor and a semiconductor
Ans:
(i) The valence band of a conductor is partially filled or it overlaps with higher energy, unoccupied conduction band.
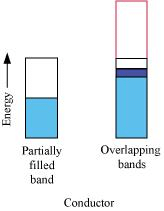
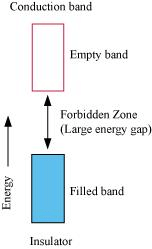
On the other hand, in the case of an insulator, the valence band is fully- filled and there is a large gap between the valence band and the conduction band.
(ii) In the case of a conductor, the valence band is partially filled or it overlaps with a higher energy, unoccupied conduction band. So, the electrons can flow easily under an applied electric field.
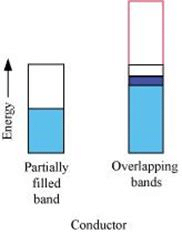
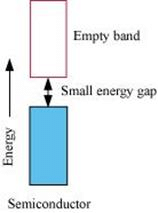
On the other hand, the valence band of a semiconductor is filled and there is a small gap between the valence band and the next higher conduction band. Therefore, some electrons can jump from the valence band to the conduction band and conduct electricity.
Q.1.19. Non-stoichiometric cuprous oxide, Cu2O can be prepared in laboratory. In this oxide, copper to oxygen ratio is slightly less than 2:1. Can you account for the fact that this substance is a p-type semiconductor?
Ans: In the cuprous oxide (Cu2O) prepared in the laboratory, copper to oxygen ratio is slightly less than 2:1. This means that the number of Cu+ ions is slightly less than twice the number of O2− ions. This is because some Cu+ ions have been replaced by Cu2+ ions. Every Cu2+ ion replaces two Cu+ ions, thereby creating holes. As a result, the substance conducts electricity with the help of these positive holes. Hence, the substance is a p-type semiconductor.
Q.1.20. Ferric oxide crystallises in a hexagonal close-packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of the ferric oxide.
Ans: Let the number of oxide (O2−) ions be x.
So, number of octahedral voids = x
It is given that two out of every three octahedral holes are occupied by ferric ions.
So, number of ferric (Fe3 ) ions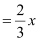
Therefore, ratio of the number of Fe3 ions to the number of O2− ions,
Fe3 : O2−
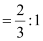
= 2 : 3
Hence, the formula of the ferric oxide is Fe2O3.
|
334 videos|651 docs|300 tests
|
FAQs on The Solid State - 2 (Old NCERT) NCERT Solutions - Chemistry for JEE Main & Advanced
| 1. What is the solid state in chemistry? |  |
| 2. What are the properties of solids? |  |
| 3. What are the different types of solids? |  |
| 4. What is the difference between amorphous and crystalline solids? |  |
| 5. How are solid-state structures determined? |  |






















