NCERT Solutions for Class 10 Maths Chapter 6 - Triangles (Exercise 6.2)
Exercise 6.2
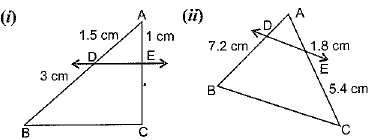
Q1. In figures (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
Sol.
(i) Given, in △ ABC, DE∥BC
∴ AD/DB = AE/EC [Using Basic proportionality theorem]
⇒ 1.5/3 = 1/EC
⇒ EC = 3/1.5
EC = 3×10/15 = 2 cm
Hence, EC = 2 cm.
(ii) Given, in △ ABC, DE∥BC
∴ AD/DB = AE/EC [Using Basic proportionality theorem]
⇒ AD/7.2 = 1.8 / 5.4
⇒ AD = 1.8 ×7.2/5.4 = (18/10)×(72/10)×(10/54) = 24/10
⇒ AD = 2.4
Hence, AD = 2.4 cm.
Q2. E and F are points on the sides PQ and PR respectively of a ΔPQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Sol.
Given, in ΔPQR, E and F are two points on side PQ and PR respectively. See the figure below;
(i) Given, PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2,4 cm
Therefore, by using Basic proportionality theorem, we get,
PE/EQ = 3.9/3 = 39/30 = 13/10 = 1.3
And PF/FR = 3.6/2.4 = 36/24 = 3/2 = 1.5
So, we get, PE/EQ ≠ PF/FR
Hence, EF is not parallel to QR.
(ii) Given, PE = 4 cm, QE = 4.5 cm, PF = 8cm and RF = 9cm
Therefore, by using Basic proportionality theorem, we get,
PE/QE = 4/4.5 = 40/45 = 8/9
And, PF/RF = 8/9
So, we get here,
PE/QE = PF/RF
Hence, EF is parallel to QR.
(iii) Given, PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
From the figure,
EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm
And, FR = PR – PF = 2.56 – 0.36 = 2.20 cm
So, PE/EQ = 0.18/1.10 = 18/110 = 9/55…………. (i)
And, PE/FR = 0.36/2.20 = 36/220 = 9/55………… (ii)
So, we get here,
PE/EQ = PF/FR
Hence, EF is parallel to QR.
Q3.In the figure, if LM || CB and LN || CD, prove that
AM/AB = AN/AD Sol.
Sol.
In the given figure, we can see, LM || CB,
By using basic proportionality theorem, we get,
AM/AB = AL/AC……………………..(i)
Similarly, given, LN || CD and using basic proportionality theorem,
∴ AN/AD = AL/AC……………………………(ii)
From equation (i) and (ii), we get,
AM/AB = AN/AD
Hence, proved.
Q4. In the figure, DE||AC and DF||AE. Prove that BF/FE = BE/EC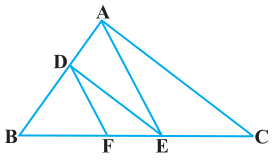 Sol.
Sol.
In ΔABC, given as, DE || AC
Thus, by using Basic Proportionality Theorem, we get,
∴ BD/DA = BE/EC ………………………………………………(i)
In ΔABC, given as, DF || AE
Thus, by using Basic Proportionality Theorem, we get,
∴ BD/DA = BF/FE ………………………………………………(ii)
From equation (i) and (ii), we get
BE/EC = BF/FE
Hence, proved.
Q5. In the figure, DE || OQ and DF || OR. Show that EF || QR.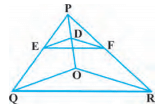 Sol.
Sol.
Given,
In ΔPQO, DE || OQ
So by using Basic Proportionality Theorem,
PD/DO = PE/EQ……………… ..(i)
Again given, in ΔPQO, DE || OQ ,
So by using Basic Proportionality Theorem,
PD/DO = PF/FR………………… (ii)
From equation (i) and (ii), we get,
PE/EQ = PF/FR
Therefore, by converse of Basic Proportionality Theorem,
EF || QR, in ΔPQR.
Q6. In the figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.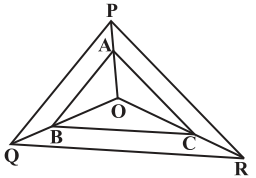 Sol.
Sol.
Given here,
In ΔOPQ, AB || PQ
By using Basic Proportionality Theorem,
OA/AP = OB/BQ…………….(i)
Also given,
In ΔOPR, AC || PR
By using Basic Proportionality Theorem
∴ OA/AP = OC/CR……………(ii)
From equation (i) and (ii), we get,
OB/BQ = OC/CR
Therefore, by converse of Basic Proportionality Theorem,
In ΔOQR, BC || QR.
Q7. Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. 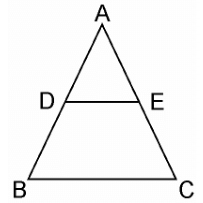 Sol.
Sol.
Given, in ΔABC, D is the midpoint of AB such that AD=DB.
A line parallel to BC intersects AC at E as shown in above figure such that DE || BC.
We have to prove that E is the mid point of AC.
Since, D is the mid-point of AB.
∴ AD=DB
⇒ AD/DB = 1 ………… (i)
In ΔABC, DE || BC,
By using Basic Proportionality Theorem,
Therefore, AD/DB = AE/EC
From equation (i), we can write,
⇒ 1 = AE/EC
∴ AE = EC
Hence, proved, E is the midpoint of AC.
Q8. Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Sol.
Given, in ΔABC, D and E are the mid points of AB and AC respectively, such that,
AD=BD and AE=EC. We have to prove that: DE || BC.
We have to prove that: DE || BC.
Since, D is the midpoint of AB
∴ AD=DB
⇒ AD/BD = 1…………. (i)
Also given, E is the mid-point of AC.
∴ AE=EC
⇒ AE/EC = 1
From equation (i) and (ii), we get,
AD/BD = AE/EC
By converse of Basic Proportionality Theorem,
DE || BC
Hence, proved.
Q9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AO/BO = CO/DO.
Sol. Given, ABCD is a trapezium where AB || DC and diagonals AC and BD intersect each other at O.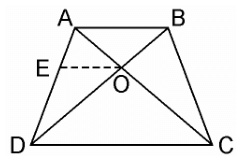
We have to prove, AO/BO = CO/DO
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB
In ΔADC, we have OE || DC
Therefore, By using Basic Proportionality Theorem
AE/ED = AO/CO ……………..(i)
Now, In ΔABD, OE || AB
Therefore, By using Basic Proportionality Theorem
DE/EA = DO/BO…………….(ii)
From equation (i) and (ii), we get,
AO/CO = BO/DO
⇒ AO/BO = CO/DO
Hence, proved.
Q10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/DO. Show that ABCD is a trapezium.
Sol.
Given, Quadrilateral ABCD where AC and BD intersects each other at O such that,
AO/BO = CO/DO.
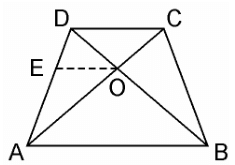 We have to prove here, ABCD is a trapezium
We have to prove here, ABCD is a trapezium
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB
In ΔDAB, EO || AB
Therefore, By using Basic Proportionality Theorem
DE/EA = DO/OB ………(i)
Also, given,
AO/BO = CO/DO
⇒ AO/CO = BO/DO
⇒ CO/AO = DO/BO
⇒ DO/OB = CO/AO ………….(ii)
From equation (i) and (ii), we get
DE/EA = CO/AO
Therefore, By using converse of Basic Proportionality Theorem,
EO || DC also EO || AB
⇒ AB || DC.
Hence, quadrilateral ABCD is a trapezium with AB || CD.
|
126 videos|457 docs|75 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 6 - Triangles (Exercise 6.2)
| 1. What are the properties of an equilateral triangle? |  |
| 2. How can we prove that two triangles are congruent? |  |
| 3. What is the Pythagorean theorem and how is it related to triangles? |  |
| 4. How can we find the area of a triangle? |  |
| 5. What is the concept of similar triangles? |  |

|
Explore Courses for Class 10 exam
|

|


















