NCERT Solutions for Class 10 Maths Chapter 7 - Coordinate Geometry (Exercise 7.2)
Q1. Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2 : 3.
Ans: Given,
Let P(x, y) be the required point.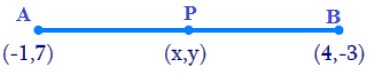 Let A(−1, 7) and B(4, −3)
Let A(−1, 7) and B(4, −3)
m: n = 2:3
Hence
x1 = −1
y1 = 7
x2 = 4
y2 = −3
By Section formula
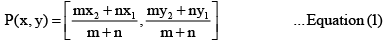
By substituting the values in the Equation (1)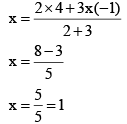
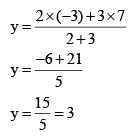
Therefore, the co-ordinates of point P are (1, 3).
Q2. Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Ans: 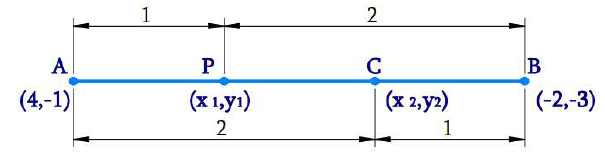
Given,
Let line segment joining the points be A(4, −1) and B(−2, −3).
Let P (x1, y1) and Q (x2, y2) be the points of trisection of the line segment joining the given points i.e., AP = PQ = QB
By Section formula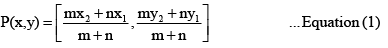
Therefore, by observation point P divides AB internally in the ratio 1:2.
Hence m: n = 1:2
By substituting the values in the Equation (1)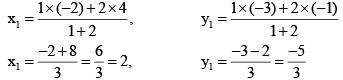
Therefore,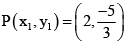
Therefore, by observation point Q divides AB internally in the ratio 2:1.
Hence m:n = 2:1
By substituting the values in the Equation (1)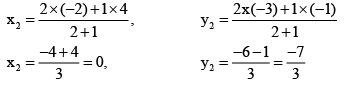
Therefore, 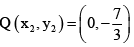
Hence the points of trisection are P(x1, y1) = 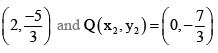
Q3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the figure. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5 th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?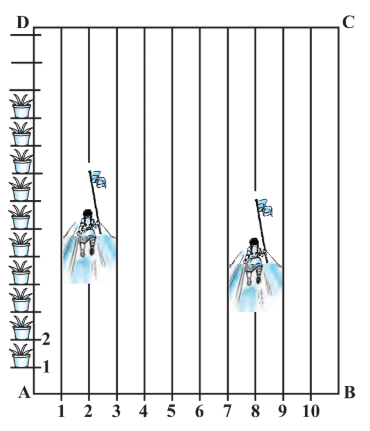 Ans: From the Figure,
Ans: From the Figure,
Given,
- By observation, that Niharika posted the green flag at of the distance P i.e.,
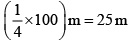 from the starting point of 2nd line. Therefore, the coordinates of this point P is (2, 25).
from the starting point of 2nd line. Therefore, the coordinates of this point P is (2, 25). - Similarly, Preet posted red flag at 1/5 of the distance
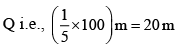 from the starting point of 8th line. Therefore, the coordinates of this point Q are (8, 20)
from the starting point of 8th line. Therefore, the coordinates of this point Q are (8, 20)
We know that the distance between the two points is given by the Distance Formula,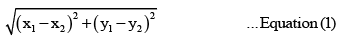
To find the distance between these flags PQ by substituting the values in Equation (1),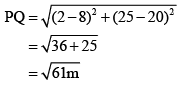
- The point at which Rashmi should post her blue flag is the mid-point of the line joining these points.
- Let this point be M (x, y).
By Section formula
Therefore, Rashmi should post her blue flag at 22.5 m on 5th line
Q4. Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Ans: From the figure, Given,
Given,
- Let the ratio in which the line segment joining A(−3, 10) and B(6, −8) is divided by point P(−1, 6) be k:1.
By Section formula
Therefore,
Hence the point P divides AB in the ratio 2:7
Q5. Find the ratio in which the line segment joining A (1, -5) and B (-4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Ans: From the Figure,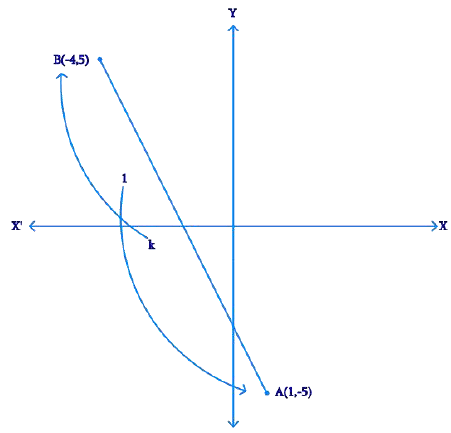 Given,
Given,
- Let the ratio be k : 1.
- Let the line segment joining A (1, −5) and B (−4, 5)
By Section formula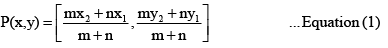
By substituting the values in Equation (1)
Therefore, the coordinates of the point of division is 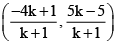
We know that y-coordinate of any point on x-axis is 0.
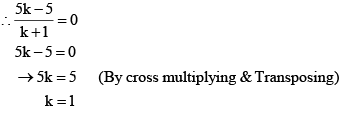
Therefore, x-axis divides it in the ratio 1:1.
Division point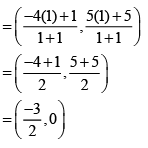
Q6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Ans: From the Figure,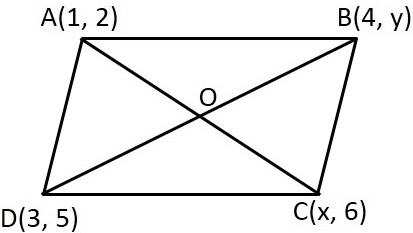
Given,
- Let A (1, 2), B (4, y), C(x, 6), and D (3, 5) are the vertices of a parallelogram ABCD.
- Since the diagonals of a parallelogram bisect each other, Intersection point O of diagonal AC and BD also divides these diagonals
Therefore, O is the mid-point of AC and BD.
If O is the mid-point of AC, then the coordinates of O are
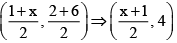
If O is the mid-point of BD, then the coordinates of O are
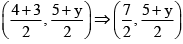
Since both the coordinates are of the same point O,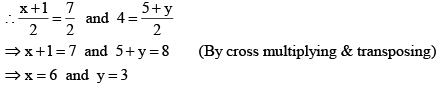
Q7. Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Ans: From the Figure,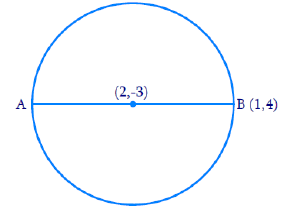
Given,
- Let the coordinates of point A be (x, y).
- Mid-point of AB is C (2, −3), which is the center of the circle.
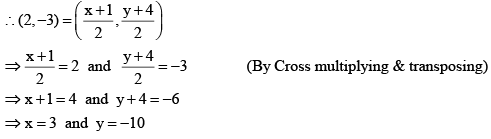
Therefore, the coordinates of A are (3, −10)
Q8. If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that  and P lies on the line segment AB.
and P lies on the line segment AB.
Ans: From the Figure,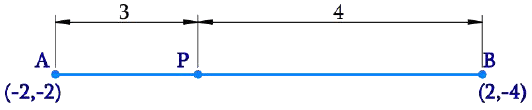 Given,
Given,
- The coordinates of point A and B are (−2, −2) and (2, −4) respectively.
- AP = 3/7AB
Hence AB/AP = 7/3
We know that AB = AP + PB from figure,
Therefore, AP:PB = 3:4
Point P(x, y) divides the line segment AB in the ratio 3:4. Using Section Formula,

Q9. Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
Ans: From the Figure,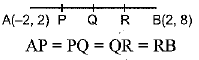
By observation, that points P, Q, R divides the line segment A (−2, 2) and B (2, 8) into four equal parts
Point P divides the line segment AQ into two equal parts
Hence, Coordinates of P = 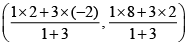
= 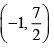
Point Q divides the line segment AB into two equal parts
Coordinates of Q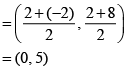
Point R divides the line segment BQ into two equal parts
Coordinates of R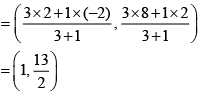
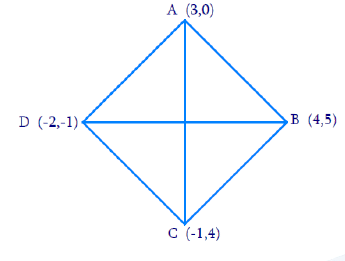
Q10. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2, -1) taken in order. [Hint: Area of a rhombus = 1/2 (product of its diagonals)]
Ans: From the Figure,
 Given,
Given,
- Let A(3, 0), B(4, 5), C(−1, 4) and D(−2, −1) are the vertices of a rhombus ABCD.
We know that the distance between the two points is given by the Distance Formula, Therefore, distance between A (3, 0) and C (−1, 4) is given by
Therefore, distance between A (3, 0) and C (−1, 4) is given by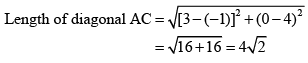
Therefore, distance between B (4, 5) and D (−2, −1) is given by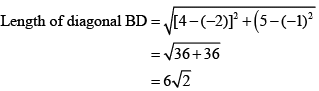
Area of the rhombus ABCD = 1/2 x (Product of lengths of diagonals)
= 1/2 AC x BD
Therefore, area of rhombus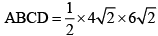
= 24 Square units
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 7 - Coordinate Geometry (Exercise 7.2)
| 1. What are the basic concepts of coordinate geometry? |  |
| 2. How do you find the distance between two points in coordinate geometry? |  |
| 3. What is the slope of a line in coordinate geometry? |  |
| 4. How do you find the midpoint of a line segment in coordinate geometry? |  |
| 5. Can you explain the concept of parallel and perpendicular lines in coordinate geometry? |  |






















