NCERT Solutions for Class 10 Maths Chapter 8 - Introduction to Trigonometry (Exercise 8.1)
Exercise 8.1
Q1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Ans:
In a given triangle ABC, right angled at B = ∠B = 90°
Given: AB = 24 cm and BC = 7 cm
According to the Pythagoras Theorem,
In a right-angled triangle, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides.
By applying the Pythagoras theorem, we get
AC2 = AB2 + BC2
AC2 = (24)2+72
AC2 = (576+49)
AC2 = 625cm2
AC = √625 = 25
Therefore, AC = 25 cm
(i) To find Sin (A), Cos (A)
We know that the sine (or) Sin function is equal to the ratio of the length of the opposite side to the hypotenuse side. So it becomes
Sin (A) = Opposite side /Hypotenuse = BC/AC = 7/25
Cosine or Cos function is equal to the ratio of the length of the adjacent side to the hypotenuse side and it becomes,
Cos (A) = Adjacent side/Hypotenuse = AB/AC = 24/25
(ii) To find Sin (C), Cos (C)
Sin (C) = AB/AC = 24/25
Cos (C) = BC/AC = 7/25
Q2. In Fig. 8.13, find tan P – cot R
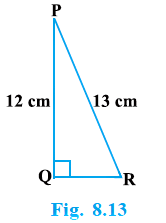
Ans:
In the given triangle PQR, the given triangle is right-angled at Q and the given measures are:
PR = 13cm,
PQ = 12cm
Since the given triangle is right-angled triangle, to find the side QR, apply the Pythagoras theorem
According to Pythagoras theorem,
In a right-angled triangle, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides.
PR2 = QR2 + PQ2
Substitute the values of PR and PQ
132 = QR2+122
169 = QR2+144
Therefore, QR2 = 169−144
QR2 = 25
QR = √25 = 5
Therefore, the side QR = 5 cm
Now, tan P – cot R=?
According to the trigonometric ratio, the tangent function is equal to the ratio of the length of the opposite side to the adjacent sides, the value of tan (P) becomes
tan (P) = Opposite side /Adjacent side = QR/PQ = 5/12
Since cot function is the reciprocal of the tan function, the ratio of cot function becomes,
Cot (R) = Adjacent side/Opposite side = QR/PQ = 5/12
Therefore,
tan (P) – cot (R) = 5/12 – 5/12 = 0
Therefore, tan(P) – cot(R) = 0
Q3. If sin A = 3/4, Calculate cos A and tan A.
Ans:
Let us assume a right-angled triangle ABC, right-angled at B
Given: Sin A = 3/4
We know that Sin function is equal to the ratio of the length of the opposite side to the hypotenuse side.
Therefore, Sin A = Opposite side /Hypotenuse= 3/4
Let BC be 3k and AC will be 4k
where k is a positive real number.
According to the Pythagoras theorem, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides of a right-angle triangle and we get,
AC2=AB2 + BC2
Substitute the value of AC and BC
(4k)2=AB2 + (3k)2
16k2−9k2 =AB2
AB2=7k2
Therefore, AB = √7k
Now, we have to find the value of cos A and tan A
We know that,
Cos (A) = Adjacent side/Hypotenuse
Substitute the value of AB and AC and cancel the constant k in both numerator and denominator, we get
AB/AC = √7k/4k = √7/4
Therefore, cos (A) = √7/4
tan(A) = Opposite side/Adjacent side
Substitute the Value of BC and AB and cancel the constant k in both numerator and denominator, we get,
BC/AB = 3k/√7k = 3/√7
Therefore, tan A = 3/√7
Q4. Given 15 cot A = 8, find sin A and sec A.
Ans:
Let us assume a right-angled triangle ABC, right-angled at B
Given: 15 cot A = 8
So, Cot A = 8/15
We know that cot function is equal to the ratio of the length of the adjacent side to the opposite side.
Therefore, cot A = Adjacent side/Opposite side = AB/BC = 8/15
Let AB be 8k and BC will be 15k
Where k is a positive real number.
According to the Pythagoras theorem, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides of a right-angle triangle and we get,
AC2=AB2 + BC2
Substitute the value of AB and BC
AC2= (8k)2 + (15k)2
AC2= 64k2 + 225k2
AC2= 289k2
Therefore, AC = 17k
Now, we have to find the value of sin A and sec A
We know that,
Sin (A) = Opposite side /Hypotenuse
Substitute the value of BC and AC and cancel the constant k in both numerator and denominator, we get
Sin A = BC/AC = 15k/17k = 15/17
Therefore, sin A = 15/17
Since secant or sec function is the reciprocal of the cos function which is equal to the ratio of the length of the hypotenuse side to the adjacent side.
Sec (A) = Hypotenuse/Adjacent side
Substitute the Value of BC and AB and cancel the constant k in both numerator and denominator, we get,
AC/AB = 17k/8k = 17/8
Therefore sec (A) = 17/8
Q5. Given sec θ = 13/12 Calculate all other trigonometric ratios
Ans:
We know that sec function is the reciprocal of the cos function which is equal to the ratio of the length of the hypotenuse side to the adjacent side
Let us assume a right-angled triangle ABC, right-angled at B
sec θ =13/12 = Hypotenuse/Adjacent side = AC/AB
Let AC be 13k and AB will be 12k
Where k is a positive real number.
According to the Pythagoras theorem, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides of a right-angled triangle and we get,
AC2=AB2 + BC2
Substitute the value of AB and AC
(13k)2= (12k)2 + BC2
169k2= 144k2 + BC2
169k2= 144k2 + BC2
BC2 = 169k2 – 144k2
BC2= 25k2
Therefore, BC = 5k
Now, substitute the corresponding values in all other trigonometric ratios
So,
Sin θ = Opposite Side/Hypotenuse = BC/AC = 5/13
Cos θ = Adjacent Side/Hypotenuse = AB/AC = 12/13
tan θ = Opposite Side/Adjacent Side = BC/AB = 5/12
Cosec θ = Hypotenuse/Opposite Side = AC/BC = 13/5
cot θ = Adjacent Side/Opposite Side = AB/BC = 12/5
Q6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B.
Ans:
Let us assume the triangle ABC in which CD⊥AB with D on AB.
Give that the angles A and B are acute angles, such that
Cos (A) = cos (B)
As per the angles taken, the cos ratio is written as
AD/AC = BD/BC
Now, interchange the terms, we get
AD/BD = AC/BC
Let take a constant value
AD/BD = AC/BC = k
Now consider the equation as
AD = k BD …(1)
AC = k BC …(2)
By applying Pythagoras theorem in △CAD and △CBD we get,
CD2 = BC2 – BD2 … (3)
CD2 =AC2 −AD2 ….(4)
From the equations (3) and (4) we get,
AC2−AD2 = BC2−BD2
Now substitute the equations (1) and (2) in (3) and (4)
K2(BC2−BD2)=(BC2−BD2) k2=1
Putting this value in equation, we obtain
AC = BC
∠A=∠B (Angles opposite to equal side are equal-isosceles triangle)
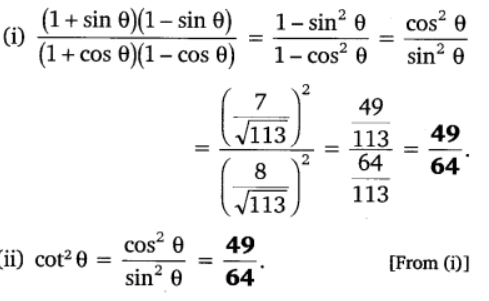
Q7. If cot θ = 7/8, evaluate:
(i) (1 + sin θ)(1 – sin θ)/(1+cos θ)(1-cos θ)
(ii) cot2 θ
Ans:
Let us assume a △ABC in which ∠B = 90° and ∠C = θ
Given:
cot θ = BC/AB = 7/8
Let BC = 7k and AB = 8k, where k is a positive real number
According to the Pythagoras theorem in △ABC we get.
AC2 = AB2+BC2
AC2 = (8k)2+(7k)2
AC2 = 64k2+49k2
AC2 = 113k2
AC = √113 k
According to the sine and cos function ratios, it is written as
sin θ = AB/AC = Opposite Side/Hypotenuse = 8k/√113 k = 8/√113 and
cos θ = Adjacent Side/Hypotenuse = BC/AC = 7k/√113 k = 7/√113
Now apply the values of sin function and cos function:
Q8. If 3 cot A = 4, check whether (1-tan2 A)/(1+tan2 A) = cos2 A – sin 2 A or not.
Ans:
Let △ABC in which ∠B=90°
We know that cot function is the reciprocal of tan function and it is written as
cot(A) = AB/BC = 4/3
Let AB = 4k and BC =3k, where k is a positive real number.
According to the Pythagoras theorem,
AC2=AB2+BC2
AC2=(4k)2+(3k)2
AC2=16k2+9k2
AC2=25k2
AC=5k
Now, apply the values corresponding to the ratios
tan(A) = BC/AB = 3/4
sin (A) = BC/AC = 3/5
cos (A) = AB/AC = 4/5
Now compare the left-hand side(LHS) with right-hand side(RHS)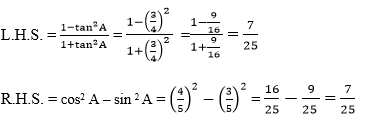
Since, both the LHS and RHS = 7/25
R.H.S. = L.H.S.
Hence, (1-tan2 A)/(1+tan2 A) = cos2 A – sin 2 A is proved
Q9. In triangle ABC, right-angled at B, if tan A = 1/√3 find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Ans:
Let ΔABC in which ∠B=90°
tan A = BC/AB = 1/√3
Let BC = 1k and AB = √3 k,
Where k is the positive real number of the problem
By Pythagoras theorem, in ΔABC we get:
AC2=AB2+BC2
AC2=(√3 k)2+(k)2
AC2=3k2+k2
AC2=4k2
AC = 2k
Now find the values of cos A, Sin A
Sin A = BC/AC = 1/2
Cos A = AB/AC = √3/2
Then find the values of cos C and sin C
Sin C = AB/AC = √3/2
Cos C = BC/AC = 1/2
Now, substitute the values in the given problem
(i) sin A cos C + cos A sin C = (1/2) ×(1/2 )+ √3/2 ×√3/2 = 1/4 + 3/4 = 1
(ii) cos A cos C – sin A sin C = (√3/2 )(1/2) – (1/2) (√3/2 ) = 0
Q10. In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P
Ans:
In a given triangle PQR, right angled at Q, the following measures are
PQ = 5 cm
PR + QR = 25 cm
Now let us assume, QR = x
PR = 25-QR
PR = 25- x
According to the Pythagoras Theorem,
PR2 = PQ2 + QR2
Substitute the value of PR as x
(25- x) 2 = 52 + x2
252 + x2 – 50x = 25 + x2
625 + x2-50x -25 – x2 = 0
-50x = -600
x= -600/-50
x = 12 = QR
Now, find the value of PR
PR = 25- QR
Substitute the value of QR
PR = 25-12
PR = 13
Now, substitute the value to the given problem
(1) Sin P = Opposite Side/Hypotenuse = QR/PR = 12/13
(2) Cos P= Adjacent Side/Hypotenuse = PQ/PR = 5/13
(3) Tan P =Opposite Side/Adjacent side = QR/PQ = 12/5
Q11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 4/3 for some angle θ.
Ans:
(i) The value of tan A is always less than 1.
False
Justification: In ΔMNC in which ∠N = 90∘,
MN = 3, NC = 4 and MC = 5
Value of tan M = 4/3 which is greater than 1.
The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as it will follow the Pythagoras theorem.
MC2 = MN2 + NC2
52 = 32 + 42
25 = 9 + 16
25 = 25
(ii) sec A = 12/5 for some value of angle A
True
Justification: Let a ΔMNC in which ∠N = 90º,
MC=12k and MB=5k, where k is a positive real number.
By Pythagoras theorem we get,
MC2=MN2+NC2
(12k)2=(5k)2+NC2
NC2+25k2=144k2
NC2=119k2
Such a triangle is possible as it will follow the Pythagoras theorem.
(iii) cos A is the abbreviation used for the cosecant of angle A.
False
Justification: Abbreviation used for cosecant of angle M is cosec M. Cos M is the abbreviation used for cosine of angle M.
(iv) cot A is the product of cot and A.
False
Justification: cot M is not the product of cot and A. It is the cotangent of ∠A.
(v) sin θ = 4/3 for some angle θ.
False
Justification: sin θ = Height/Hypotenuse
We know that in a right-angled triangle, Hypotenuse is the longest side.
∴ sin θ will always be less than 1 and it can never be 4/3 for any value of θ.
Exercise 8.2
Q1. Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60
Solution:
(i) The values of the given trigonometric ratios:
sin 30° = 1/2, cos 30° = √3/2, sin 60° = 3/2, cos 60°= 1/2
Now, substitute the values in the given problem
sin 60° cos 30° + sin 30° cos 60° = √3/2 ×√3/2 + (1/2) ×(1/2 ) = 3/4+1/4 = 4/4 = 1
(ii) The values of the trigonometric ratios:
sin 60° = √3/2, cos 30° = √3/2, tan 45° = 1
Substitute the values in the given problem
2 tan2 45° + cos2 30° – sin2 60 = 2(1)2 + (√3/2)2-(√3/2)2 = 2 + 0 = 2
(iii) We know that:
cos 45° = 1/√2, sec 30° = 2/√3, cosec 30° = 2
Substitute the values, we get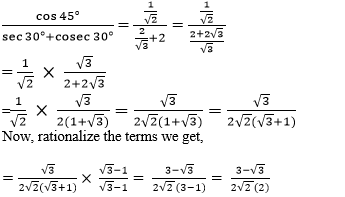
Now, multiply both the numerator and denominator by √2, we get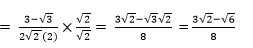
Therefore, cos 45°/(sec 30°+cosec 30°) = (3√2 – √6)/8
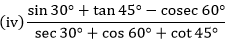
We know that,
sin 30° = 1/2, tan 45° = 1, cosec 60° = 2/√3, sec 30° = 2/√3, cos 60° = 1/2, cot 45° = 1
Substitute the values in the given problem, we get
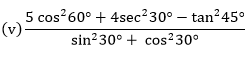
We know that,
cos 60° = 1/2, sec 30° = 2/√3, tan 45° = 1, sin 30° = 1/2, cos 30° = √3/2
Now, substitute the values in the given problem, we get
(5cos260° + 4sec230° – tan245°)/(sin2 30° + cos2 30°)
= 5(1/2)2 + 4(2/√3)2 - 12/(1/2)2 + (√3/2)2 = (5/4 + 16/3 - 1)/(1/4 + 3/4) = {(15 + 64 - 12)/12}/(4/4) = 67/12
Q2. Choose the correct option and justify your choice:
(i) 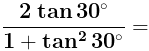
(a) sin 60°
(b) cos 60°
(c) tan 60°
(d) sin 30°
Ans. (A) is correct
Justification: Substitute tan 30° = 1/√3 in the given equation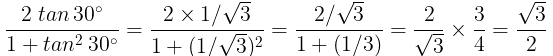
∵ √3/2 = sin 60°
The obtained solution is equivalent to the trigonometric ratio sin 60°
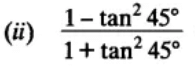
(a) tan 90°
(b) 1
(c) sin 45°
(d) 0
Ans. (D) is correct
Justification:
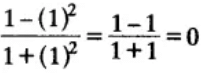
(iii) sin 2A = 2 sin A is true when A =
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Ans. (A) is correct.
Justification: To find the value of A, substitute the degree given in the options one by one
sin 2A = 2 sin A is true when A = 0°
As, sin 2A = sin 0° = 0 and 2 sin A = 2 sin 0° = 2 × 0 = 0
or,
Apply the sin 2A formula, to find the degree value
sin 2A = 2sin A cos A
⇒ 2sin A cos A = 2 sin A
⇒ 2cos A = 2 ⇒ cos A = 1
Now, we have to check, to get the solution as 1, which degree value has to be applied.
When 0 degree is applied to cos value, i.e., cos 0 = 1
Therefore, ⇒ A = 0°
(iv) 
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
Ans. (C) is correct.
Justification: 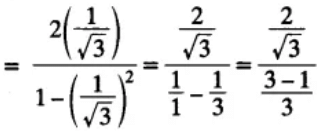
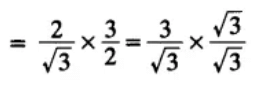
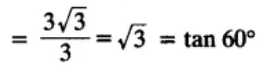
Q3. If tan (A + B) = √3 and tan (A – B) = 1/√3 ,0° < A + B ≤ 90°; A > B, find A and B.
Solution:
tan (A + B) = √3
Since √3 = tan 60°
Now substitute the degree value
⇒ tan (A + B) = tan 60°
(A + B) = 60° … (i)
The above equation is assumed as equation (i)
tan (A – B) = 1/√3
Since 1/√3 = tan 30°
Now substitute the degree value
⇒ tan (A – B) = tan 30°
(A – B) = 30° … equation (ii)
Now add the equation (i) and (ii), we get
A + B + A – B = 60° + 30°
Cancel the terms B
2A = 90°
A= 45°
Now, substitute the value of A in equation (i) to find the value of B
45° + B = 60°
B = 60° – 45°
B = 15°
Therefore A = 45° and B = 15°
Q4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
Ans. False
Justification: Let us take A = 30° and B = 60°, then
Substitute the values in the sin (A + B) formula, we get
sin (A + B) = sin (30° + 60°) = sin 90° = 1 and,
sin A + sin B = sin 30° + sin 60°
= 1/2 + √3/2 = 1+√3/2
Since the values obtained are not equal, the solution is false.
(ii) The value of sin θ increases as θ increases.
Ans. True
Justification: According to the values obtained as per the unit circle, the values of sin are: sin 0° = 0, sin 30° = 1/2, sin 45° = 1/√2, sin 60° = √3/2, sin 90° = 1
Thus the value of sin θ increases as θ increases. Hence, the statement is true
(iii) The value of cos θ increases as θ increases.
Ans. False
Justification: According to the values obtained as per the unit circle, the values of cos are: cos 0° = 1, cos 30° = √3/2, cos 45° = 1/√2, cos 60° = 1/2, cos 90° = 0
Thus, the value of cos θ decreases as θ increases. So, the statement given above is false.
(iv) sin θ = cos θ for all values of θ.
Ans. False
Justification: sin θ = cos θ, when a right triangle has 2 angles of (π/4). Therefore, the above statement is false.
(v) cot A is not defined for A = 0°.
Ans. True
Justification: Since cot function is the reciprocal of the tan function, it is also written as:
cot A = cos A/sin A
Now substitute A = 0°
cot 0° = cos 0°/sin 0° = 1/0 = undefined.
Hence, it is true
Exercise 8.3
Q1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:
To convert the given trigonometric ratios in terms of cot functions, use trigonometric formulas
We know that,
cosec2A – cot2A = 1
cosec2A = 1 + cot2A
Since cosec function is the inverse of sin function, it is written as
1/sin2A = 1 + cot2A
Now, rearrange the terms, it becomes
sin2A = 1/(1+cot2A)
Now, take square roots on both sides, we get
sin A = ±1/(√(1+cot2A)
The above equation defines the sin function in terms of cot function
Now, to express sec function in terms of cot function, use this formula
sin2A = 1/ (1+cot2A)
Now, represent the sin function as cos function
1 – cos2A = 1/ (1+cot2A)
Rearrange the terms,
cos2A = 1 – 1/(1+cot2A)
⇒cos2A = (1-1+cot2A)/(1+cot2A)
Since sec function is the inverse of cos function,
⇒ 1/sec2A = cot2A/(1+cot2A)
Take the reciprocal and square roots on both sides, we get
⇒ sec A = ±√ (1+cot2A)/cotA
Now, to express tan function in terms of cot function
tan A = sin A/cos A and cot A = cos A/sin A
Since cot function is the inverse of tan function, it is rewritten as
tan A = 1/cot A
Q2. Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Cos A function in terms of sec A:
sec A = 1/cos A
⇒ cos A = 1/sec A
sec A function in terms of sec A:
cos2A + sin2A = 1
Rearrange the terms
sin2A = 1 – cos2A
sin2A = 1 – (1/sec2A)
sin2A = (sec2A-1)/sec2A
sin A = ± √(sec2A-1)/sec A
cosec A function in terms of sec A:
sin A = 1/cosec A
⇒cosec A = 1/sin A
cosec A = ± sec A/√(sec2A-1)
Now, tan A function in terms of sec A:
sec2A – tan2A = 1
Rearrange the terms
⇒ tan2A = sec2A + 1
tan A = √(sec2A + 1)
cot A function in terms of sec A:
tan A = 1/cot A
⇒ cot A = 1/tan A
cot A = ±1/√(sec2A + 1)
Q3. Choose the correct option. Justify your choice.
(i) 9 sec2A – 9 tan2A =
(a) 1
(b) 9
(c) 8
(d) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(a) 0
(b) 1
(c) 2
(d) – 1
(iii) (sec A + tan A) (1 – sin A) =
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
(iv) 1+tan2A/1+cot2A =
(a) sec2 A
(b) -1
(c) cot2A
(d) tan2A
Solution:
(i) (B) is correct.
Justification:
Take 9 outside, and it becomes
9 sec2A – 9 tan2A
= 9 (sec2A – tan2A)
= 9×1 = 9 (∵ sec2 A – tan2 A = 1)
Therefore, 9 sec2A – 9 tan2A = 9
(ii) (C) is correct
Justification:
(1 + tan θ + sec θ) (1 + cot θ – cosec θ)
We know that, tan θ = sin θ/cos θ
sec θ = 1/ cos θ
cot θ = cos θ/sin θ
cosec θ = 1/sin θ
Now, substitute the above values in the given problem, we get
= (1 + sin θ/cos θ + 1/ cos θ) (1 + cos θ/sin θ – 1/sin θ)
Simplify the above equation,
= (cos θ +sin θ+1)/cos θ × (sin θ+cos θ-1)/sin θ
= (cos θ+sin θ)2-12/(cos θ sin θ)
= (cos2θ + sin2θ + 2cos θ sin θ -1)/(cos θ sin θ)
= (1+ 2cos θ sin θ -1)/(cos θ sin θ) (Since cos2θ + sin2θ = 1)
= (2cos θ sin θ)/(cos θ sin θ) = 2
Therefore, (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =2
(iii) (D) is correct.
Justification:
We know that,
Sec A= 1/cos A
Tan A = sin A / cos A
Now, substitute the above values in the given problem, we get
(secA + tanA) (1 – sinA)
= (1/cos A + sin A/cos A) (1 – sinA)
= (1+sin A/cos A) (1 – sinA)
= (1 – sin2A)/cos A
= cos2A/cos A = cos A
Therefore, (secA + tanA) (1 – sinA) = cos A
(iv) (D) is correct.
Justification:
We know that,
tan2A =1/cot2A
Now, substitute this in the given problem, we get
1+tan2A/1+cot2A
= (1+1/cot2A)/1+cot2A
= (cot2A+1/cot2A)×(1/1+cot2A)
= 1/cot2A = tan2A
So, 1+tan2A/1+cot2A = tan2A
Q4. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ – cot θ)2 = (1-cos θ)/(1+cos θ)
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]
(iv) (1 + sec A)/sec A = sin2A/(1-cos A)
[Hint : Simplify LHS and RHS separately]
(v) ( cos A–sin A+1)/( cos A +sin A–1) = cosec A + cot A, using the identity cosec2A = 1+cot2A.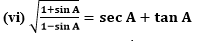
(vii) (sin θ – 2sin3θ)/(2cos3θ-cos θ) = tan θ
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
[Hint : Simplify LHS and RHS separately]
(x) (1+tan2A/1+cot2A) = (1-tan A/1-cot A)2 = tan2A
Solution:
(i) (cosec θ – cot θ)2 = (1-cos θ)/(1+cos θ)
To prove this, first take the Left-Hand side (L.H.S) of the given equation, to prove the Right Hand Side (R.H.S)
L.H.S. = (cosec θ – cot θ)2
The above equation is in the form of (a-b)2, and expand it
Since (a-b)2 = a2 + b2 – 2ab
Here a = cosec θ and b = cot θ
= (cosec2θ + cot2θ – 2cosec θ cot θ)
Now, apply the corresponding inverse functions and equivalent ratios to simplify
= (1/sin2θ + cos2θ/sin2θ – 2cos θ/sin2θ)
= (1 + cos2θ – 2cos θ)/(1 – cos2θ)
= (1-cos θ)2/(1 – cosθ)(1+cos θ)
= (1-cos θ)/(1+cos θ) = R.H.S.
Therefore, (cosec θ – cot θ)2 = (1-cos θ)/(1+cos θ)
Hence proved.
(ii) (cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A
Now, take the L.H.S of the given equation.
L.H.S. = (cos A/(1+sin A)) + ((1+sin A)/cos A)
= [cos2A + (1+sin A)2]/(1+sin A)cos A
= (cos2A + sin2A + 1 + 2sin A)/(1+sin A) cos A
Since cos2A + sin2A = 1, we can write it as
= (1 + 1 + 2sin A)/(1+sin A) cos A
= (2+ 2sin A)/(1+sin A)cos A
= 2(1+sin A)/(1+sin A)cos A
= 2/cos A = 2 sec A = R.H.S.
L.H.S. = R.H.S.
(cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A
Hence proved.
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
L.H.S. = tan θ/(1-cot θ) + cot θ/(1-tan θ)
We know that tan θ =sin θ/cos θ
cot θ = cos θ/sin θ
Now, substitute it in the given equation, to convert it in a simplified form
= [(sin θ/cos θ)/1-(cos θ/sin θ)] + [(cos θ/sin θ)/1-(sin θ/cos θ)]
= [(sin θ/cos θ)/(sin θ-cos θ)/sin θ] + [(cos θ/sin θ)/(cos θ-sin θ)/cos θ]
= sin2θ/[cos θ(sin θ-cos θ)] + cos2θ/[sin θ(cos θ-sin θ)]
= sin2θ/[cos θ(sin θ-cos θ)] – cos2θ/[sin θ(sin θ-cos θ)]
= 1/(sin θ-cos θ) [(sin2θ/cos θ) – (cos2θ/sin θ)]
= 1/(sin θ-cos θ) × [(sin3θ – cos3θ)/sin θ cos θ]
= [(sin θ-cos θ)(sin2θ+cos2θ+sin θ cos θ)]/[(sin θ-cos θ)sin θ cos θ]
= (1 + sin θ cos θ)/sin θ cos θ
= 1/sin θ cos θ + 1
= 1 + sec θ cosec θ = R.H.S.
Therefore, L.H.S. = R.H.S.
Hence proved
(iv) (1 + sec A)/sec A = sin2A/(1-cos A)
First find the simplified form of L.H.S
L.H.S. = (1 + sec A)/sec A
Since secant function is the inverse function of cos function and it is written as
= (1 + 1/cos A)/1/cos A
= (cos A + 1)/cos A/1/cos A
Therefore, (1 + sec A)/sec A = cos A + 1
R.H.S. = sin2A/(1-cos A)
We know that sin2A = (1 – cos2A), we get
= (1 – cos2A)/(1-cos A)
= (1-cos A)(1+cos A)/(1-cos A)
Therefore, sin2A/(1-cos A)= cos A + 1
L.H.S. = R.H.S.
Hence proved
(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A, using the identity cosec2A = 1+cot2A.
With the help of identity function, cosec2A = 1+cot2A, let us prove the above equation.
L.H.S. = (cos A–sin A+1)/(cos A+sin A–1)
Divide the numerator and denominator by sin A, we get
= (cos A–sin A+1)/sin A/(cos A+sin A–1)/sin A
We know that cos A/sin A = cot A and 1/sin A = cosec A
= (cot A – 1 + cosec A)/(cot A+ 1 – cosec A)
= (cot A – cosec2A + cot2A + cosec A)/(cot A+ 1 – cosec A) (using cosec2A – cot2A = 1
= [(cot A + cosec A) – (cosec2A – cot2A)]/(cot A+ 1 – cosec A)
= [(cot A + cosec A) – (cosec A + cot A)(cosec A – cot A)]/(1 – cosec A + cot A)
= (cot A + cosec A)(1 – cosec A + cot A)/(1 – cosec A + cot A)
= cot A + cosec A = R.H.S.
Therefore, (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A
Hence Proved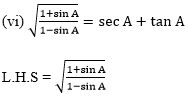
First divide the numerator and denominator of L.H.S. by cos A,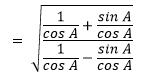
We know that 1/cos A = sec A and sin A/ cos A = tan A and it becomes,
= √(sec A+ tan A)/(sec A-tan A)
Now using rationalization, we get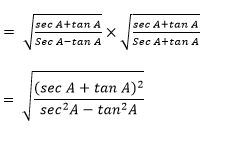
= (sec A + tan A)/1
= sec A + tan A = R.H.S
Hence proved
(vii) (sin θ – 2sin3θ)/(2cos3θ-cos θ) = tan θ
L.H.S. = (sin θ – 2sin3θ)/(2cos3θ – cos θ)
Take sin θ as in numerator and cos θ in denominator as outside, it becomes
= [sin θ(1 – 2sin2θ)]/[cos θ(2cos2θ- 1)]
We know that sin2θ = 1-cos2θ
= sin θ[1 – 2(1-cos2θ)]/[cos θ(2cos2θ -1)]
= [sin θ(2cos2θ -1)]/[cos θ(2cos2θ -1)]
= tan θ = R.H.S.
Hence proved
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A
L.H.S. = (sin A + cosec A)2 + (cos A + sec A)2
It is of the form (a+b)2, expand it
(a+b)2 =a2 + b2 +2ab
= (sin2A + cosec2A + 2 sin A cosec A) + (cos2A + sec2A + 2 cos A sec A)
= (sin2A + cos2A) + 2 sin A(1/sin A) + 2 cos A(1/cos A) + 1 + tan2A + 1 + cot2A
= 1 + 2 + 2 + 2 + tan2A + cot2A
= 7+tan2A+cot2A = R.H.S.
Therefore, (sin A + cosec A)2 + (cos A + sec A)2 = 7+tan2A+cot2A
Hence proved.
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A + cotA)
First, find the simplified form of L.H.S
L.H.S. = (cosec A – sin A)(sec A – cos A)
Now, substitute the inverse and equivalent trigonometric ratio forms
= (1/sin A – sin A)(1/cos A – cos A)
= [(1-sin2A)/sin A][(1-cos2A)/cos A]
= (cos2A/sin A)×(sin2A/cos A)
= cos A sin A
Now, simplify the R.H.S
R.H.S. = 1/(tan A+cotA)
= 1/(sin A/cos A +cos A/sin A)
= 1/[(sin2A+cos2A)/sin A cos A]
= cos A sin A
L.H.S. = R.H.S.
(cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
Hence proved
(x) (1+tan2A/1+cot2A) = (1-tan A/1-cot A)2 = tan2A
L.H.S. = (1+tan2A/1+cot2A)
Since cot function is the inverse of tan function,
= (1+tan2A/1+1/tan2A)
= 1+tan2A/[(1+tan2A)/tan2A]
Now cancel the 1+tan2A terms, we get
= tan2A
(1+tan2A/1+cot2A) = tan2A
Similarly,
(1-tan A/1-cot A)2 = tan2A
Hence proved
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 8 - Introduction to Trigonometry (Exercise 8.1)
| 1. What is the basic concept of trigonometry? |  |
| 2. How is trigonometry used in real life? |  |
| 3. What are the primary trigonometric ratios? |  |
| 4. How do you find the trigonometric ratios of an angle? |  |
| 5. What are the applications of trigonometry in solving problems? |  |






















