NCERT Solutions for Class 6 Maths Chapter 5 - Understanding Elementary Shapes
| Table of contents |

|
| Exercise 5.1 |

|
| Exercise 5.2 |

|
| Exercise 5.3 |

|
| Exercise 5.4 |

|
| Exercise 5.5 |

|
| Exercise 5.6 |

|
| Exercise 5.7 |

|
| Exercise 5.8 |

|
Exercise 5.1
Q1. What is the disadvantage in comparing line segments by mere observation?
Ans: We will be using the concept of line segments to solve this.
In the given figure, line segment PQ and RS seem to be equal but actually, they are not equal.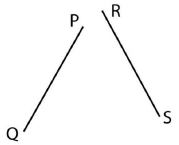 The disadvantage of comparing the lengths of two line segments by mere observation is that the lengths might not be accurate. Hence, a divider is used to compare the lengths of the line segments.
The disadvantage of comparing the lengths of two line segments by mere observation is that the lengths might not be accurate. Hence, a divider is used to compare the lengths of the line segments.
Q2. Why is it better to use a divider than a ruler, while measuring the length of a line segment?
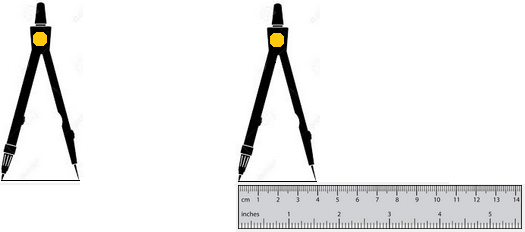
Ans: It is often better to use a divider than a ruler to measure the length of a line segment because:
 Divider & Ruler
Divider & Ruler
More Accurate: A divider helps you mark the exact endpoints of a line segment without worrying about lining up a ruler perfectly. This makes the measurement more accurate.
No Viewing Mistakes: With a ruler, you have to look directly from above to read the measurement correctly. If you look from the side, it might look different. A divider avoids this problem since you only need to set its points on the ends of the line segment.
Easy to Measure with a Ruler: After you mark the length on the divider, you can place it on a ruler to measure the distance easily.
So, a divider can help you measure line segments more accurately and easily!
Q3. Draw any line segment, say 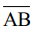 . Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AB = AC + CB?
. Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AB = AC + CB?
[Note : If A,B,C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B]
Ans: We will be using the concept of the line segment to solve this. Let us consider the line AB with point C being in the center of A and B and AB = 7 cm.
Let us consider the line AB with point C being in the center of A and B and AB = 7 cm.
AC = 3 cm
CB = 4 cm
Therefore, AC + CB = 3 cm + 4 cm
AC + CB = 7 cm.
But, AB = 7 cm.
Hence, AB = AC + CB
Q4. If A, B, C are three points on a line such that AB = 5 cm, BC = 3 cm and AC = 8 cm, which one of them lies between the other two?
Ans: We will be using the concept of line segments to solve this.
We have, AB = 5 cm
BC = 3 cm
Therefore, AB + BC = 5 + 3
AB + BC = 8 cm
But, AC = 8 cm
Hence, B lies between A and C.
Q5. Verify, whether D is the mid point of 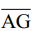 .
.
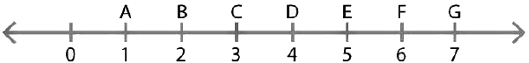 Ans: We will be using the concept of midpoint to solve this.
Ans: We will be using the concept of midpoint to solve this.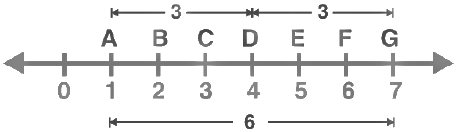 From the given figure,
From the given figure,
We have,
AG = 7 cm – 1 cm
AG = 6 cmAD = 4 cm – 1 cm
AD = 3 cm
DG = 7 cm – 4 cm
DG = 3 cm
AD + DG = 3cm + 3cm
AD + DG = 6 cm
Therefore, AG = AD + DG
Where, AD = DG = 3cm
Hence, D is the midpoint of AG
Q6. If B is the mid-point of  and C is the midpoint of
and C is the midpoint of  , where A, B, C, D lie on a straight line, say why AB = CD?
, where A, B, C, D lie on a straight line, say why AB = CD?
Ans: We will be using the concept of midpoint to solve this.
We have been given that, B is the midpoint of AC
⇒ AB = BC ----------------- (1)
C is the midpoint of BD
⇒ BC = CD --------------- (2)
Hence, we can say that AB = CD [From equation(1) and equation(2)]
Q7. Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Ans: We will be using the concept of triangles to solve this.
Case I. In ∆ABC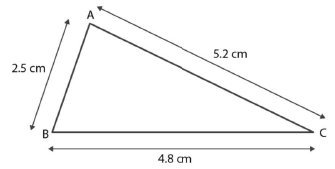 Consider:
Consider:
AB = 2.5 cm
BC = 4.8 cm
AC = 5.2 cm
AB + BC = 2.5 cm + 4.8 cm
AB + BC = 7.3 cm
Since, 7.3 > 5.2 , AB + BC > AC
Therefore, the sum of any two sides of a triangle is greater than the third side.
Case II. In ∆PQR,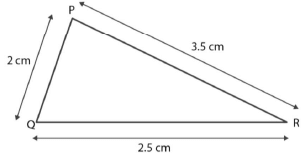 Consider:
Consider:
PQ = 2 cm
QR = 2.5 cm
PR = 3.5 cm
PQ + QR = 2 cm + 2.5 cm
PQ + QR = 4.5 cm
Since, 4.5 > 3.5, PQ + QR > PR
Therefore, the sum of any two sides of a triangle is greater than the third side.
Case III. In ∆XYZ,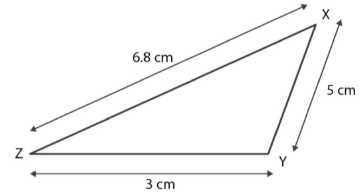 Consider
Consider
XY = 5 cm
YZ = 3 cm
ZX = 6.8 cm
XY + YZ = 5 cm + 3 cm
XY + YZ = 8 cm
Since, 8 > 6.8, XY + YZ > ZX
Therefore, the sum of any two sides of a triangle is greater than the third side.
Case IV. In ∆MNS,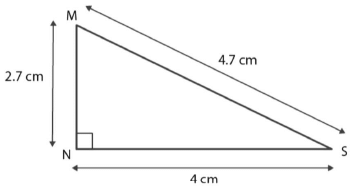 Consider
Consider
MN = 2.7 cm
NS = 4 cm
MS = 4.7 cm
MN + NS = 2.7 cm + 4 cm
MN + NS = 6.7 cm
Since, 6.7 >4.7, MN + NS > MS
Hence, the sum of any two sides of a triangle is greater than the third side.
Case V. In ∆KLM,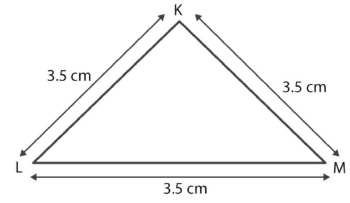 Consider
Consider
KL = 3.5 cm
LM = 3.5 cm
KM = 3.5 cm
L + LM = 3.5 cm + 3.5 cm
L + LM = 7 cm
7 cm > 3.5 cm, KL + LM > KM
Therefore, the sum of any two sides of a triangle is greater than the third side. Hence, we conclude that the sum of any two sides of a triangle is never less than the third side.
Exercise 5.2
Q1. What fraction of a clockwise revolution does the hour hand of a clock turn through, when it goes from
(a) 3 to 9
(b) 4 to 7
(c) 7 to 10
(d) 12 to 9
(e) 1 to 10
(f) 6 to 3
Hint: To find the portion of the clock swept by the hour hand between any two numbers(hours) say 'a' and 'b' where b > a will be found by subtracting 'a' from 'b' i.e, b - a.
Also, to find the fraction of a clockwise revolution between 'a' and 'b' we now divide the portion of the clock swept by the hour hand between them by 12 (since, the clock is divided into 12 equal divisions) Hence, the fraction will be (b - a) / 12 Using this concept, let's solve the given problems.
(a) 3 to 9
Ans: Lets first subtract 3 from 9 and then divide the answer by 12
9 – 3 = 6 ÷ 12 = 1/2 of a clockwise revolution
(b) 4 to 7
Ans: Lets first subtract 4 from 7 and then divide the answer by 12
7 – 4 = 3 ÷ 12 = 1/4 of a clockwise revolution
(c) 7 to 10
Ans: Lets first subtract 7 from 10 and then divide the answer by 12
10 – 7 = 3 ÷ 12 = 1/4 of a clockwise revolution
(d) 12 to 9
Ans: i.e., 0 to 9 [Since, 12 is at 0th position of the clock]
Lets first subtract 0 from 9 and then divide the answer by 12
9 – 0 = 9 ÷ 12 = 3/4 of a clockwise revolution
(e) 1 to 10
Ans: Lets first subtract 1 from 10 and then divide the answer by 12
10 – 1 = 9 ÷ 12 = 3/4 of a clockwise revolution
(f) 6 to 3
Ans: i.e., 6 to 12 and then 12 to 3
6 to 12 = 12 – 6 = 6 and 12 to 3 = 0 to 3 = 3 – 0 = 3
6 + 3 = 9 ÷ 12 = 3/4 of a clockwise revolution
Q2. Where will the hand of a clock stop if it
(a) starts at 12 and makes 1/2 of a revolution, clockwise?
Ans: When the clock hand starts from 12 and makes ½ of a revolution, the clock hand stops at 6.
1 revolution = 12 hours
1/2 revolution = 6 hours
Hence, the clock will land at 6.
(b) starts at 2 and makes 1/2 of a revolution, clockwise?
Ans: When the clock hand starts from 2 and makes ½ of a revolution, the clock hand stops at 8
1 revolution = 12 hours
1/2 revolution = 6 hours
Hence, the clock will land at 2 + 6 = 8.
(c) starts at 5 and makes 1/4 of a revolution, clockwise?
Ans: When the clock hand starts from 5 and makes 1/4 of a revolution, the clock hand stops at 8
1 revolution = 12 hours
1/4 revolution = 3 hours
Hence, the clock will land at (5 + 3) = 8.
(d) starts at 5 and makes 3/4 of a revolution, clockwise?
Ans: When the clock hand starts from 5 and makes 3/4 of a revolution, the clock hand stops at 2.
1 revolution = 12 hours
3/4 revolution = 9 hours
Hence, the clock will land at (5 + 9) = 14
Which is 2 hours added to 12 so the answer is 2 o'clock.
Q3. Which direction will you face if you start facing
(a) East and make ½ of a revolution clockwise?
(b ) East and make 1 ½ of a revolution clockwise?
(c) West and make ¾ of a revolution anti-clockwise?
(d) South and make one full revolution?
(Should we specify clockwise or anticlockwise for this last question? Why not?)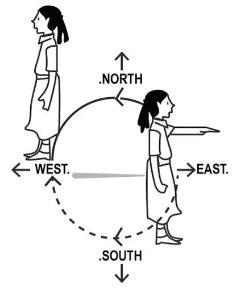 (a) East and make ½ of a revolution clockwise?
(a) East and make ½ of a revolution clockwise?
Ans: If we start facing East and make ½ of a revolution clockwise, we will be facing the West direction.
1 revolution = 360 degrees
1/2 revolution = 180 degrees
Thus, we start from East, move 180 degrees clockwise and stop at West.
(b) East and make 1 ½ of a revolution clockwise?
Ans: If we start facing East and make 1 ½ revolution clockwise, we will be facing the West direction.
1 revolution = 360 degrees
1/2 revolution = 180 degrees
Hence, 1 ½ revolution = 360 + 180 = 1 revolution + another 1/2 revolution
Thus, we start from East, move 360 degrees clockwise to complete 1 revolution, and continue moving for another 180 degrees to cover 1/2 revolution and stop at West.
(c) West and make ¾ of a revolution anti-clockwise?
Ans: If we start facing the West and make ¾ revolution anticlockwise, we will be facing the North direction.
1 revolution = 360 degrees
3/4 revolution = 270 degrees = 1/2 revolution + 1/4 revolution (180 degrees + 90 degrees)
Thus, we start from West, move 180 degrees anti-clockwise to complete 1/2 revolution till East, and continue moving for another 90 degrees to cover 1/4 revolution anti-clockwise and stop at North.
(d) South and make one full revolution?
Ans: It does not matter if we turn clockwise or anticlockwise, taking one full revolution will make it a full revolution and reach back to the starting position.
Thus, after 1 complete revolution that is 360 degrees, we stop at the same point from where we had started i.e, South.
Q4. What part of a revolution have you turned through if you stand facing
(a) east and turn clockwise to face north?
Ans: If we start from east and turn clockwise to face north,3/4 of a revolution is required, as seen in the image below.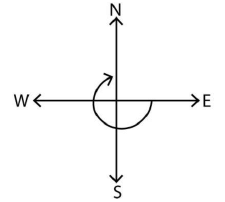
(b) south and turn clockwise to face east?
Ans: If we start from the south and turn clockwise to face east, 3/4 of a revolution is required.
(c) west and turn clockwise to face east?
Ans: If we start from the west and turn clockwise to face east, 1/2 of a revolution is required.
Q5. Find the number of right angles turned through by the hour hand of a clock when it goes from
(a) 3 to 6
Ans: 3 to 6 - The hour hand turns through 1 right angle starting from 3 to 6.
(b) 2 to 8
Ans: 2 to 8 - The hour hand turns through 2 right angles starting from 2 to 8.
(c) 5 to 11
Ans: 5 to 11- The hour hand turns through 2 right angles starting from 5 to 11.
(d) 10 to 1
Ans: 10 to 1 - The hour hand turns through 1 right angle starting from 10 to 1.
(e) 12 to 9
Ans: 12 to 9 - The hour hand turns through 3 right angles starting from 12 to 9.
(f) 12 to 6
Ans: 12 to 6 - The hour hand turns through 2 right angles starting from 12 to 6.
Q6. How many right angles do you make if you start facing
(a) south and turn clockwise to west?
Ans: The number of right angles made while facing the south and turning clockwise to the west is 1 right angle.
(b) north and turn anticlockwise to east?
Ans: The number of right angles made while facing the north and turning anticlockwise to the east is 3 right angles.
(c) west and turn to the west?
Ans: The number of right angles made while facing the west and turning to the west is 4 right angles.
(d) south and turn to north?
Ans: The number of right angles made while facing the south and turning to the north is 2 right angles.
Q7. Where will the hour hand of a clock stop if it starts
(a) from 6 and turns through 1 right angle?
(b) from 8 and turns through 2 right angles?
(c) from 10 and turns through 3 right angles?
(d) from 7 and turns through 2 straight angles?
(a) from 6 and turns through 1 right angle?
Ans: We know that in 1 complete revolution in either clockwise or anticlockwise direction, hour hand of a clock will rotate by 360o or 4 right angles
(a) If hour hand of a clock starts from 6 and turns through 1 right angle, it will stop at 9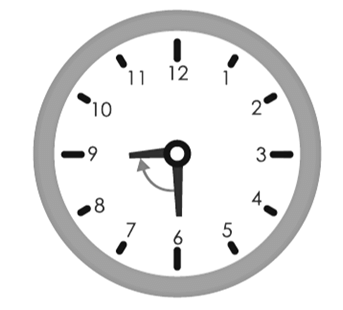
(b) If hour hand of a clock starts from 8 and turns through 2 right angles, it will stop at 2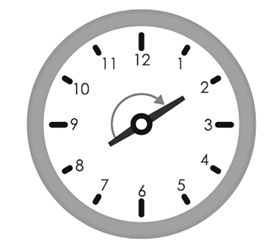
(c) If hour hand of a clock starts from 10 and turns through 3 right angles, it will stop at 7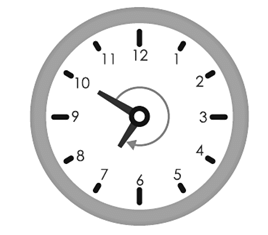
(d) If hour hand of a clock starts from 7 and turns through 2 straight angles, it will stop at 7
Exercise 5.3
Q1. Match the following:
Ans: We will use the concept of angles to solve this.
Q2. Classify each one of the following angles as right, straight, acute, obtuse or reflex: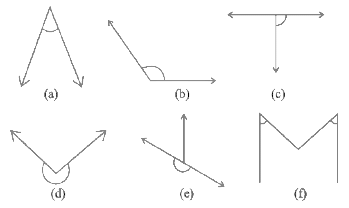 Ans: We will use the concept of angles to solve this.
Ans: We will use the concept of angles to solve this.
(a) Acute angle - It is less than 90°
(b) Obtuse angle - It is greater than 90° but less than 180°
(c) Right angle - It is equal to 90°
(d) Reflex angle - It is greater than 180° but less than 360°
(e) Straight angle - It is equal to 180°
(f) Acute angle - It is less than 90°
Exercise 5.4
Q1. What is the measure of
(i) a right angle?
Ans: The measure of a right angle is 90o
(ii) a straight angle?
Ans: The measure of a straight angle is 180o
Q2. Say True or False:
(a) The measure of an acute angle < 90°.
(b) The measure of an obtuse angle < 90°.
(c) The measure of a reflex angle > 180°.
(d) The measure of on complete revolution = 360°.
(e) If m∠A = 53o and m∠B = 35o then m∠A > m∠B.
Ans:
(a) True; the measure of an acute angle is less than 90o
(b) False; the measure of an obtuse angle is more than 90o but less than 180o
(c) True; the measure of a reflex angle is more than 180o
(d) True; the measure of one complete revolution is 360o
(e) True; ∠A is greater than ∠B
Q3. Write down the measure of:
(a) some acute angles
(b) some obtuse angles
(give at least two examples of each)
Ans: (a) The measures of an acute angle are 50°, 65°
(b) The measures of obtuse angle are 110°, 175°
Q4. Measure the angles given below using the Protractor and write down the measure: 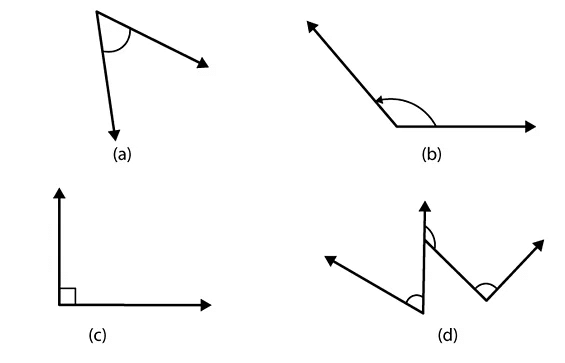
Ans: (a) The measure of an angle is 45°
(b) The measure of an angle is 120°
(c) The measure of an angle is 90°
(d) The measures of angles are 60°, 90° and 130°
Q5. Which angle has a large measure? First estimate and then measure:
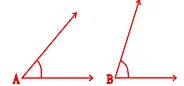 Measure of angle A = ?
Measure of angle A = ?
Measure of angle B = ?
Ans: ∠B has larger measure.
∠A = 40o and ∠B = 68o
Q6. From these two angles which has larger measure? Estimate and then confirm by measuring them:
Ans: Second angle has larger measure.
The measures of these angles are 45o and 55o.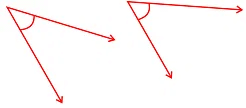
Q7. Fill in the blanks with acute, obtuse, right or straight:
(a) An angle whose measure is less than that of a right angle is ________________.
Ans: acute angle
(b) An angle whose measure is greater than that of a right angle is ________________.
Ans: obtuse angle
(c) An angle whose measure is the sum of the measures of two right angles is ________________.
Ans: straight angle
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is ________________.
Ans: acute angle
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be ________________.
Ans: obtuse angle
Q8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor.) 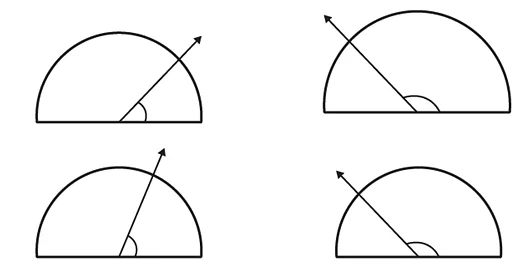
Ans: The measures of the angles shown in the above figures are 40o, 130o, 65o and 135o
Q9. Find the angle measure between the hands of the clock in each figure:
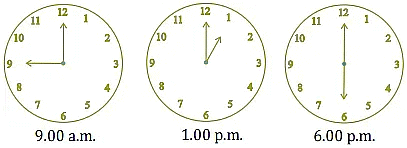 Ans: (i) 90 (Right angle)
Ans: (i) 90 (Right angle)
(ii) 30 (Acute angle)
(iii) 180 (Straight angle)
Q10. Investigate:
In the given figure, the angle measure 30o. Look at the same figure through a magnifying glass. Does the angle becomes larger? Does the size of the angle change?
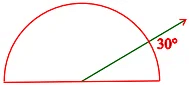
Ans: No, the measure of angle will be same.
Q11. Measure and classify each angle:
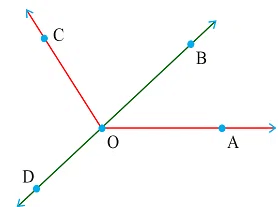
Ans: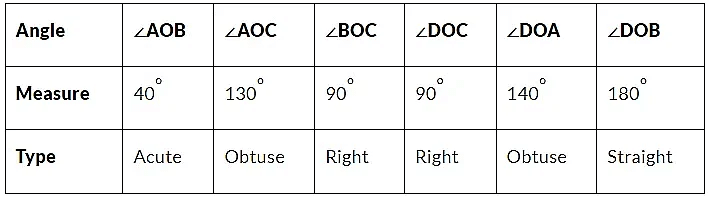
Exercise 5.5
Q1. Which of the following are models for perpendicular lines:
(a) The adjacent edges of a table top.
(b) The lines of a railway track.
(c) The line segments forming the letter ‘L’.
(d) The letter V.
Ans:
(a) Perpendicular
(b) Not perpendicular
(c) Perpendicular
(d) Not perpendicular
Q2. Let 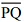 be the perpendicular to the line segment
be the perpendicular to the line segment 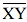 . Let
. Let 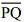 and
and 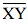 intersect in the point A. What is the measure of ∠PAY?
intersect in the point A. What is the measure of ∠PAY?
Ans: We will be using the concept of perpendicular lines to solve this.
Since PQ ⊥ XY Therefore, ∠PAY = 90°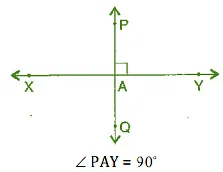
Q3. There are two “set-squares” in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
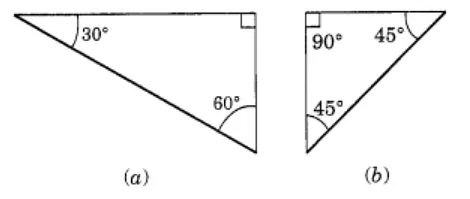
Ans: One set-square has 60°,90°, 30° and other set-square has 45° ,90° ,45°. They have 90° as common angle.
Q4. Study the diagram. The line l is perpendicular to line m.
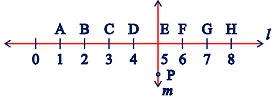
(a) Is CE = EG?
(b) Does PE bisect CG?
(c) Identify any two line segments for which PE is the perpendicular bisector.
(d) Are these true?
(i) AC > FG
(ii) CD = GH
(iii) BC < EH
Ans: (a) Yes, both measure 2 units.
(b) Yes, because CE = EG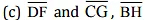 (d) (i) True, (ii) True, (iii) True
(d) (i) True, (ii) True, (iii) True
Exercise 5.6
Q1. Name the types of following triangles:
(a) Triangle with lengths of sides 7 cm, 8 cm and 9 cm.
(b) ΔABC with AB = 8.7 cm, AC = 7 cm and BC = 6 cm.
(c) ΔPQR such that PQ = QR = PR = 5 cm.
(d) ΔDEF with m∠D = 90o
(e) ΔXYZ with m∠Y = 90o and XY = YZ
(f) ΔLMN with m∠L = 30o , m∠M = 70o and m∠N = 80o.
Ans: (a) Scalene triangle
(b) Scalene triangle
(c) Equilateral triangle
(d) Right-angled triangle
(e) Isosceles right-angled triangle
(f) Acute-angled triangle
Q2. Match the following:
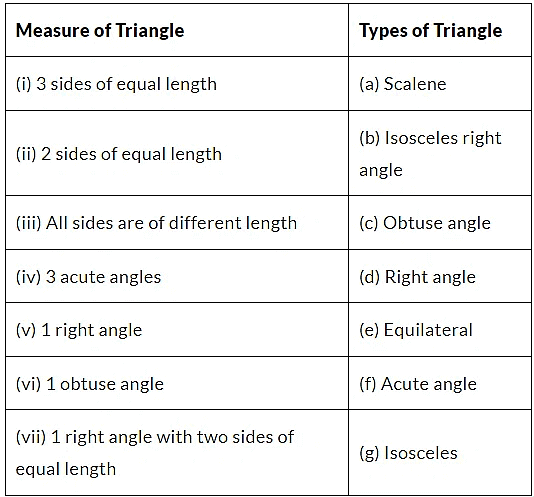
Ans: (i) → (e)
(ii) → (g)
(iii) → (a)
(iv) → (f)
(v) → (d)
(vi) → (c)
(vii) → (b)
Q3. Name each of the following triangles in two different ways: (You may judge the nature of angle by observation) 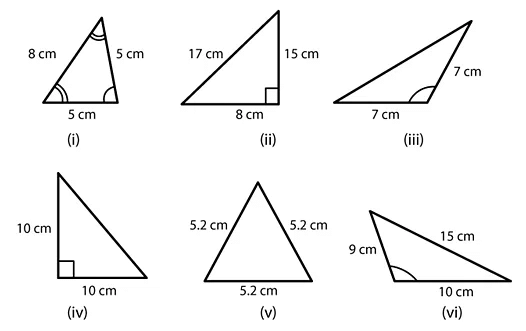
Ans: (i) Acute-angled and isosceles triangle
(ii) Right-angled and scalene triangle
(iii) Obtuse-angled and isosceles triangle
(iv) Right-angled and isosceles triangle
(v) Equilateral and acute-angled triangle
(vi) Obtuse-angled and scalene triangle
Q4. Try to construct triangles using match sticks. Some are shown here.
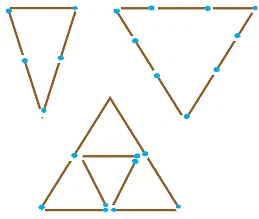
Can you make a triangle with:
(a) 3 matchsticks?
(b) 4 matchsticks?
(c) 5 matchsticks?
(d) 6 matchsticks?
(Remember you have to use all the available matchsticks in each case)
If you cannot make a triangle, think of reasons for it.
Ans: (a) 3 matchsticks This is an acute angle triangle and it is possible with 3 matchsticks to make a triangle because sum of two sides is greater than third side.
(b) 4 matchsticks This is a square, hence with four matchsticks we cannot make triangle.
(c) 5 matchsticks This is an acute angle triangle and it is possible to make triangle with five matchsticks, in this case sum of two sides is greater than third side.
(d) 6 matchsticks This is an acute angle triangle and it is possible to make a triangle with the help of 6 matchsticks because sum of two sides is greater than third side.
Exercise 5.7
Q1. Say true or false:
(a) Each angle of a rectangle is a right angle.
(b) The opposite sides of a rectangle are equal in length.
(c) The diagonals of a square are perpendicular to one another.
(d) All the sides of a rhombus are of equal length.
(e) All the sides of a parallelogram are of equal length.
(f) The opposite sides of a trapezium are parallel.
Ans: (a) True
(b) True
(c) True
(d) True
(e) False
(f) False
Q2. Give reasons for the following:
(a) A square can be thought of as a special rectangle.
(b) A rectangle can be thought of as a special parallelogram.
(c) A square can be thought of as a special rhombus.
(d) Squares, rectangles, parallelograms are all quadrilateral.
(e) Square is also a parallelogram.
Ans: (a) Because its all angles are right angle and opposite sides are equal.
(b) Because its opposite sides are equal and parallel.
(c) Because its four sides are equal and diagonals are perpendicular to each other.
(d) Because all of them have four sides.
(e) Because its opposite sides are equal and parallel.
Q3. A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Ans: A square is a regular quadrilateral because all the interior angles are 90o, and all sides are of the same length.
Exercise 5.8
Q1. Examine whether the following are polygons. If anyone among these is not, say why?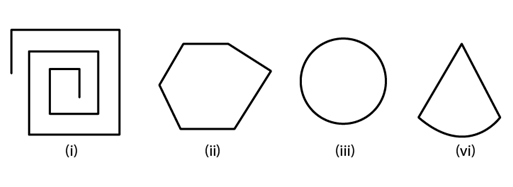 Ans: (a) As it is not a closed figure, therefore, it is not a polygon.
Ans: (a) As it is not a closed figure, therefore, it is not a polygon.
(b) It is a polygon because it is closed by line segments.
(c) It is not a polygon because it is not made by line segments.
(d) It is not a polygon because it not made only by line segments, it has curved surface also.
Q2. Name each polygon: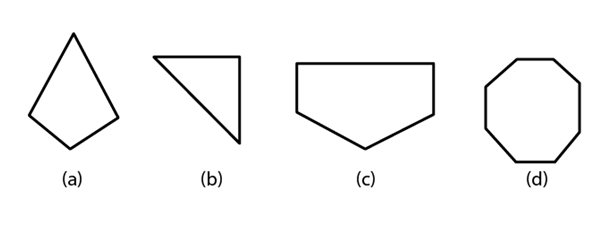 Make two more examples of each of these.
Make two more examples of each of these.
Ans: (a) Quadrilateral
(b) Triangle
(c) Pentagon
(d) Octagon
Q3. Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.
Ans: ABCDEF is a regular hexagon and triangle thus formed by joining AEF is an isosceles triangle.
Q4. Draw a rough sketch of a regular octagon. (Use squared paper if you wish). Draw a rectangle by joining exactly four of the vertices of the octagon.
Ans: ABCDEFGH is a regular octagon and CDGH is a rectangle.
Q5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
Ans: ABCDE is the required pentagon and its diagonals are AD, AC, BE and BD.
|
82 videos|273 docs|69 tests
|
FAQs on NCERT Solutions for Class 6 Maths Chapter 5 - Understanding Elementary Shapes
| 1. What are the basic geometric shapes covered in Understanding Elementary Shapes? |  |
| 2. How do you calculate the area of a rectangle? |  |
| 3. What is the difference between a square and a rectangle? |  |
| 4. How can we identify different types of triangles? |  |
| 5. Why is it important to understand the properties of geometric shapes? |  |
















