NCERT Solutions for Class 8 Maths - Algebraic Expressions and Identities - 1 (Exercise 8.1 and 8.2)

Exercise 8.1

Q1. Add the following:
(i) ab – bc, bc – ca, ca – ab
Ans: (ab – bc) + (bc – ca) + (ca-ab)
= ab – bc + bc – ca + ca – ab
= ab – ab – bc + bc – ca + ca
= 0

(ii) a – b + ab, b – c + bc, c – a + ac
Ans: (a – b + ab) + (b – c + bc) + (c – a + ac)
= a – b + ab + b – c + bc + c – a + ac
= a – a +b – b +c – c + ab + bc + ca
= 0 + 0 + 0 + ab + bc + ca
= ab + bc + ca

(iii) 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²

Ans: 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²
= (2p²q² – 3pq + 4) + (5 + 7pq – 3p²q²)
= 2p²q² – 3p²q² – 3pq + 7pq + 4 + 5
= – p²q² + 4pq + 9

(iv) l² + m², m² + n², n² + l², 2lm + 2mn + 2nl
Ans: (l² + m²) + (m² + n²) + (n² + l²) + (2lm + 2mn + 2nl)
= l² + l² + m² + m² + n² + n² + 2lm + 2mn + 2nl
= 2l² + 2m² + 2n² + 2lm + 2mn + 2nl

Q2. (a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
Ans: (12a – 9ab + 5b – 3) – (4a – 7ab + 3b + 12)
= 12a – 9ab + 5b – 3 – 4a + 7ab – 3b – 12
= 12a – 4a -9ab + 7ab +5b – 3b -3 -12
= 8a – 2ab + 2b – 15

(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
Ans: (5xy – 2yz – 2zx + 10xyz) – (3xy + 5yz – 7zx)
= 5xy – 2yz – 2zx + 10xyz – 3xy – 5yz + 7zx
=5xy – 3xy – 2yz – 5yz – 2zx + 7zx + 10xyz
= 2xy – 7yz + 5zx + 10xyz

(c) Subtract 4p²q – 3pq + 5pq² – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq² + 5p²q
Ans: (18 – 3p – 11q + 5pq – 2pq² + 5p²q) – (4p²q – 3pq + 5pq² – 8p + 7q – 10)
= 18 – 3p – 11q + 5pq – 2pq² + 5p²q – 4p²q + 3pq – 5pq² + 8p – 7q + 10
=18+10 -3p+8p -11q – 7q + 5 pq+ 3pq- 2pq² – 5pq^2 + 5 p^2 q – 4p^2 q
= 28 + 5p – 18q + 8pq – 7pq² + p²q

Exercise 8.2

Q1: Find the product of the following pairs of monomials. 
(i) 4, 7p 
Ans: 4 , 7 p =  4 × 7 × p = 28p

(ii) –4p, 7p 
Ans: – 4p × 7p = (-4 × 7 ) × (p × p )= -28p²

(iii) –4p, 7pq
Ans: – 4p × 7pq =(-4 × 7 ) (p × pq) =  -28p²q

(iv) 4p³, –3p 
Ans: 4p³ × – 3p = (4 × -3 ) (p³ × p ) =  -12p4

(v) 4p, 0
Ans: 4p ×  0 = 0

Q2: Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np)
Ans: Area of rectangle = Length x breadth. So, it is the multiplication of two monomials.
The results can be written in square units.
(i) p × q = pq
(ii)10m ×  5n = 50mn
(iii) 20x² ×  5y² =  100x²y²
(iv) 4x × 3x² = 12x³
(v) 3mn ×  4np = 12mn²p

Q3: Complete the table of products.

Ans: The table can be completed as follows.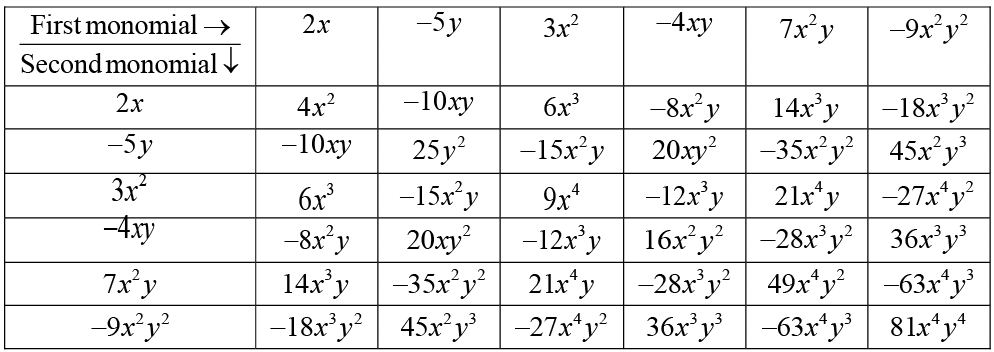

Q4. Obtain the volume of rectangular boxes with the following length, breadth and height respectively.

Volume of rectangle = length x  breadth x  height. To evaluate volume of rectangular boxes, multiply all the monomials.
(i) 5a, 3a², 7a⁴ 
Ans:  5a × 3a² × 7a⁴ = (5 × 3 × 7) (a × a² × a⁴ ) = 105a⁷

^{(ii) 2p, 4q, 8r}
Ans: 2p × 4q × 8r = (2 × 4 × 8 ) (p × q × r ) = 64pqr

(iii) xy, 2x²y, 2xy² 
Ans: y × 2x²y × 2xy² =(1 × 2 × 2 )( x × x² × x × y × y × y² ) =  4x⁴y⁴

^{(iv) a, 2b, 3c}
Ans: a x  2b x 3c = (1 × 2 × 3 ) (a × b × c) = 6abc

Q5. Obtain the product of
(i) xy, yz, zx
Ans: xy × yz × zx = x² y² z²

^{(ii) a, – a2, a3} 
Ans: a × – a²  × a³ = – a⁶

^{(iii) 2, 4y, 8y2, 16y3} 
Ans: 2 × 4y × 8y² × 16y³ = 1024 y⁶

^{(iv) a, 2b, 3c, 6abc}
Ans: a × 2b × 3c × 6abc = 36a² b² c²

^{(v) m, – mn, mnp}
Ans: m × – mn × mnp = –m³ n² p

Old NCERT Questions

Q1: Identify the terms, their coefficients for each of the following expressions.

(i) 5xyz² – 3zy

Ans:

(ii) 1 + x + x²

^Ans:

(iii) 4x²y² – 4x²y²z² + z²

^Ans:

(iv) 3 – pq + qr – rp

Ans:

(v) x/2 +x/2 - xy

Ans:

(vi) 0.3a – 0.6ab + 0.5b

Ans:

Q2: Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?

x + y, 1000,   x + x² + x³ + x⁴,   7 + y + 5x, 2y – 3y²,   2y – 3y² + 4y³,
5x – 4y + 3xy,   4z – 15z²,   ab + bc + cd + da, pqr,   p²q + pq², 2p + 2q

Sol: 

Following polynomials do not fit in any of these categories:

x + x² + x³ + x² [∵ It has 4 terms.]

ab + bc + cd + da [∵ It has 4 terms.]