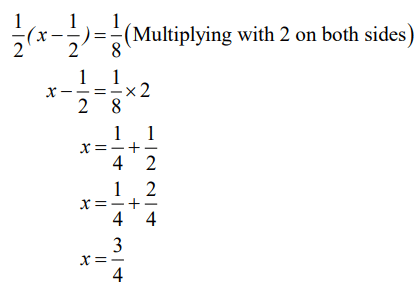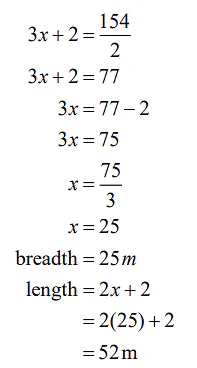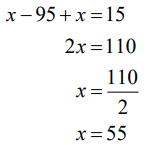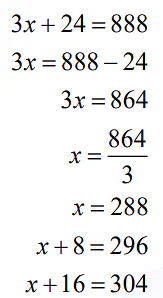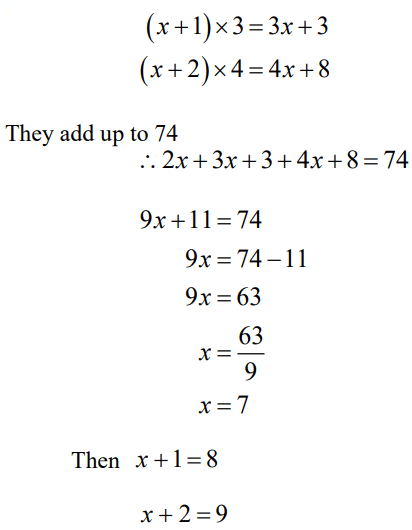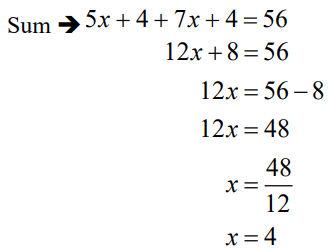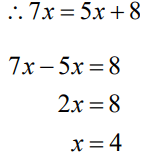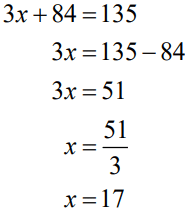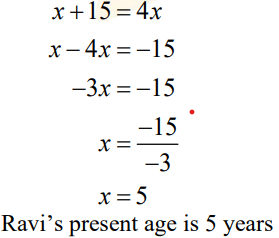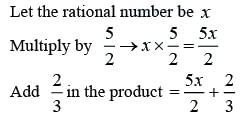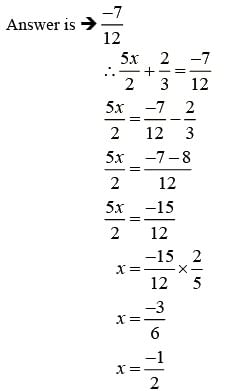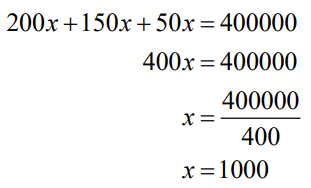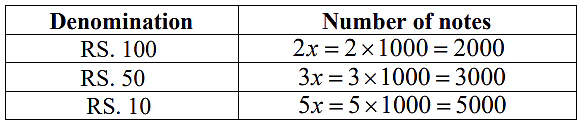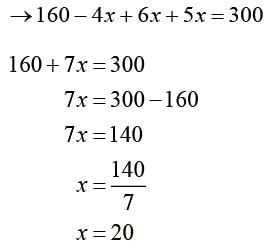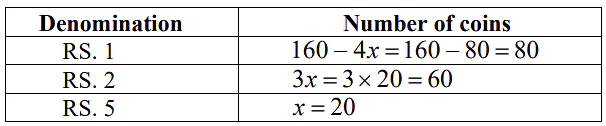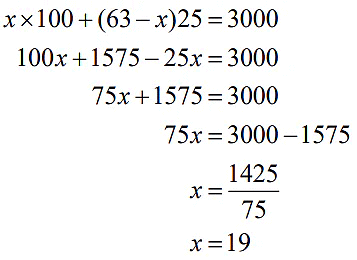NCERT Solutions for Class 8 Maths Chapter 2 - Ex 2.2 Linear Equations in One Variable

Q1. If you subtract 1/2 from a number and multiply the result by 1/2 , you get 1/8 . What is the number?
Answer:
Difficulty Level: MediumWhat is known or given?
- is subtracted from a number.
- Result is multiplied by 1/2
- Answer is 1/ 8
What is the unknown?
- The number
Reasoning:
Forming a linear equation for the given problem statement and solving it will lead to the solution
Step 1:
Let the number be xStep 2:
1/2 is subtracted from a number → x − 1/2
Step 3:
Result is multiplied by 12 → 1 2 ( x − 1/2)
Answer is 1/8 → 1/2 ( x − 1/2 ) = 1/ 8
Solving:
The number is 3/4.
Q2. The perimeter of a rectangular swimming pool is 154 m. Its length is 2 m more than twice its breadth. What are the length and the breadth of the pool?
Answer:
Difficulty Level: Medium
What is the known/given?
- Perimeter of a rectangular swimming pool is 154m.
- Its length is 2m more than twice its breadth.
What is the unknown?
- Length and breadth of the pool.
Reasoning:
Form a linear equation by using the formula for the perimeter of a rectangle. Assume either the breadth or the length to be a variable
Step 1:
Let the breadth of swimming pool be x m.Therefore, the length of the swimming pool will be (2x + 2) m
Step 2:
Perimeter of rectangular swimming pool: 2(Length +Breadth)
Therefore, 2( x + 2 x + 2) =154
Length of the pool = 52m
Breadth of the pool = 25m
Q3. The base of an isosceles triangle is 4/3 cm. The perimeter of the triangle is 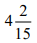 cm. What is the length of either of the remaining equal sides?
cm. What is the length of either of the remaining equal sides?
Answer:
Difficulty Level: Medium
What is the known/given?
- Base of an isosceles triangle = 4/3 cm
- Perimeter of the triangle =
cm
What is the unknown?
Length of sides of the equal sides of isosceles triangle.
Reasoning:
In an isosceles triangle, two sides of the triangle are equal. The value of one side is given. We can assume any one of the two sides to be a variable and form a linear equation using the following formula for the perimeter of any triangle:
Perimeter of a Triangle = Sum of the Lengths of all Three Sides
Step 1:
Let the length of either of equal sides be x cm.
Step 2:
Base of an isosceles triangle = 4/3 cm
Step 3:
Perimeter of the triangle → x + x + 4/3 =
(adding all these sides)
Length of either of the equal side of isosceles triangle is 7/5 cm
Q4. Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
Answer:
Difficulty Level: Medium
What is the known/given?
- Some of two numbers is 95.
- One exceeds the other by 15.
What is the unknown?
- Numbers
Reasoning:
Assume any one number to be a variable and form a linear equation by using the relationships between the two numbers mentioned in the problem statement.
Step 1:
Let one of the numbers be x .
Then the other number ➔95 – x (as sum of them is 95).
Step 2:
If we assume x to be larger among two of them.
x − (95 − x) =15 (as one exceeds other by 15)
Then other number ➔95 − x = 95 − 55 = 40
The numbers are 40 and 55.
Q5. Two numbers are in the ratio 5:3. If they differ by 18, what are the numbers?
Answer:
Difficulty Level: Medium
What is the known/given?
- Two number are in ratio 5:3.
- They differ by 18.
What is the unknown?
- Number
Reasoning:
Assume any one number to be a variable and form a linear equation by using the relationships between the two numbers as mentioned in the problem statement. Any one relationship will allow you to express one number in terms of the other number (assumed to be a variable first). Then, the second relationship will allow you to form a linear equation.
Two number are in ratio 5:3
∴The number are 5x and 3x.
The two numbers differ by 18:
5x − 3 x =18
2 x =18
x = 9
First number is 5x = 5 x9 = 45
Second number is 3x = 3x9 = 27
The numbers will be 45 and 27.
Q6. Three consecutive integers add up to 51. What are these integers?
Answer:
Difficulty Level: Medium
What is the known/given?
- Three consecutive integers add up to 51.
What is the unknown?
- Integers.
Reasoning:
Assume one integer to be a variable. Then use the property of consecutive integers and the given condition to form a linear equation.
Step 1:
Let the first integer be x.
Then next consecutive two integers are x + 1 and x + 2
Three consecutive integers are 16, 17 and 18.
Q7. The sum of three consecutive multiples of 8 is 888. Find the multiples.
Answer:
Difficulty Level: Medium
What is the known/given?
- Sum of three consecutive multiples of 8 is 888.
What is the unknown?
- Multiples.
Reasoning:
Assume one multiple to be a variable. Then use the property of consecutive multiples to form a linear equation.
Step 1:
Let the first multiple be xThen second consecutive multiple of 8➔ x + 8
Third consecutive multiple of 8 ➔ x + 8 + 8 = x +16
Step 2:
The multiples are 288, 296 and 304.
Q8. Three consecutive integers are such that when they are taken in increasing order and multiplied by 2, 3 and 4 respectively, they add up to 74. Find these numbers.
Answer:
Difficulty Level: Hard
What is the known/given?
- Three consecutive integers are such that when they are taken in increasing order and multiplied by 2, 3 and 4 respectively, they add up to 74.
What is the unknown?
- Number.
Reasoning:
Assume one integer to be a variable. Then use the property of consecutive integers and the given condition to form a linear equation.
Step 1:
Let the first integer be x.Step 2:
Next two consecutive integers are x + 1 and x + 2
They are taken in increasing order and multiplied by 2,3 and 4 respectively.
The numbers are 7, 8 and 9.
Q9. The ages of Rahul and Haroon are in the ratio 5:7. Four years later the sum of their ages will be 56 years. What are their present ages?
Answer:
Difficulty Level: Medium
What is the known/given?
- Ages of Rahul and Haroon are in ratio 5 :7
- Four years later, sum of their ages will be 56 years.
What is the unknown?
- Present ages of Rahul and Haroon.
Reasoning:
Assume the age of either Rahul or Haroon as a variable. Use the first condition to express the ages in terms of the variable. Then use the second condition to form a linear equation.
Step 1:
Ages of Rahul and Haroon are in ratio 5 :7
Present ages of Rahul and Haroon are 5x and 7x respectively.
Four years later, sum of their ages will be 56 years.
Four years later, age of Rahul = 5x + 4
Four years later, age of Haroon = 7x + 4
Step 2:
Present age of Rahul = 5x = 5x4 = 20
Present age of Haroon = 7x = 7x4 = 28
Present age of Rahul and Haroon are 20 and 28 years respectively.
Q10. The number of boys and girls in a class are in the ratio 7:5. The number of boys is 8 more than the number of girls. What is the total class strength?
Answer:
Difficulty Level: Medium
What is the known/given?
- Number of boys and girls in a class are in ratio 7:5
- Number of boys is 8 more than the number of girls.
What is the unknown?
- Total class strength.
Reasoning:
Use the first condition to express the numbers in terms of the variable. Use the second condition to form a linear equation.
Step 1:
Number of boys and girls in a class are in ratio 7:5Number of boys in class = 7x
Number of girls in class = 5x
Number of boys is 8 more than number of girls.
Number of boys in class = 7x = 7x4 = 28
Number of girls in class = 5x = 5x4 = 20
Total class strength = number of boys + number of girls
=28+20= 48
Total class strength is 48 students.
Q11. Baichung’s father is 26 years younger than Baichung’s grandfather and 29 years older than Baichung. The sum of the ages of all the three is 135 years. What is the age of each one of them?
Answer:
Difficulty Level: Hard
What is the known/given?
- Baichung’s father is 26 years younger than Baichung’s grandfather and
- 29 years older than Baichung
- Sum of the ages of all the three is 135 years.
What is the unknown?
- Ages of Baichung, Baichung’s father and Baichung’s grandfather.
Reasoning:
Assume Baichung’s age to be a variable. Then use the first condition to express the ages of Baichung’s father and grandfather. Finally, use the last second condition to form a linear equation.
Step 1:
Let the age of Baichung be x years.
Age of Baichung’s father = x + 29 years as he is 29 years older than Baichung.
Age of Baichung’s grandfather = age of Baichung father + 26 years
[ ∴ Since Baichung’s father is 26 years younger than Baichung’s grandfather]
x + 29 + 26
x + 55YearsSum of ages of all the three is 135 years.
∴ x + x + 29 + x + 55 =135
Ages: Baichung father grandfathers.
Age of Baichung is 17 years
Age of Baichung’s father is x + 29 = 17 + 29 = 46 years
Age of Baichung’s grandfathers is x + 55 = 17 + 55 = 72 years
Q12. Fifteen years from now Ravi’s age will be four times his present age. What is Ravi’s present age?
Answer:
Difficulty Level: Medium
What is the known/given?
- Fifteen years from now Ravi’s age will be four times his present age.
What is the unknown?
- Ravi’s present age
Reasoning:
Assume Ravi’s age to be a variable. Use the first and second condition to express his age after 15 years in the form of a linear equation.
Step 1:
Let the present age of Ravi be x years.15 years from now, Ravi’s age will be 4 times his present age
Step 2:
Q13. A rational number is such that when you multiply it by 5/2 and add 2/3 to the product, you get − 7/12 . What is the number?
Answer:
Difficulty Level: Medium
What is the known/given?
- A rational number is such that when multiply it by 5/2 and add 2/3 to the product, you get − 7/12
What is the unknown?
- Numbers.
Reasoning:
Assume the rational number to be a variable. Apply the conditions sequentially to form a linear equation.
Q14. Lakshmi is a cashier in a bank. She has currency notes of denomination Rs.100, Rs.50 and Rs.10, respectively. The ratio of the number of these notes is 2:3:5. The total cash with Lakshmi is Rs.4,00,000. How many notes of each denomination does she have?
Answer:
Difficulty Level: Hard
Reasoning:
Use the ratio condition and express the number of notes of different denominations in terms of a variable. Use the second condition to form a linear equation.
What is the known/given?
- Cashier Lakshmi has currency notes of denominaton Rs. 100, Rs.50, and Rs.10
- Ratio of the number of notes is 2:3:5.
- Total cash with Lakshmi is Rs. 4,00,000
What is the unknown?
- How many notes of each denomination.
Reasoning:
Use the ratio condition and express the number of notes of different denominations in terms of a variable. Use the second condition to form a linear equation.
Step 1:
Step 2:
- Lakshmi has currency notes of denomination Rs.100, Rs.50, Rs.10.
- Number of notes are in ratio 2:3:5, therefore number of notes is 2x, 3x and 5x
Step 3:
Q15. I have a total of Rs. 300 in coins of denomination Rs.1, Rs.2 and Rs.5. The number of Rs. 2 coins is 3 times the number of Rs.5 coins. The total number of coins is 160. How many coins of each denomination are with me?
Answer:
Difficulty Level: HardWhat is the known/given?
- Total amount = RS. 300
- Coin denominations are Rs. 1, Rs.2 and Rs. 5
- Number of Rs.2 coins are 3 times Rs. 5 coins.
- Total coins ➔160
What is the unknown?
- How many coins of each denominations are there.
Reasoning:
Assume the number of Rs. 5 coin to be a variable. Use the second condition to obtain the number of coins for Rs 2 in terms of the variable. Use the third condition to find the number of coins for Rs 1. Finally, use the first condition to form a linear equation.
Step 1:
Let the number of Rs 5 coins be x.Step 2:
Then the number of Rs.2 coins is 3x.
Number of Rs.1 coin is = 160 − ( x + 3 x) [as total coins are 160]
=160 − 4x
Q16. The organizers of an essay competition decide that a winner in the competition gets a prize of Rs.100 and a participant who does not win gets a prize of Rs. 25. The total prize money distributed is Rs.3,000. Find the number of winners, if the total number of participants is 63.
Answer:
Difficulty Level: Hard
What is the known/given?
- Winner of essay competition gets a prize of Rs 100
- Participant who does not win gets a prize of Rs 25
- Total prize of money distributed is Rs. 3000
- Total number of participants is 63.
What is the unknown?
- Number of winners.
Reasoning: Assume the total number of winners is x. As total number of participants is 63, number of participants who did not win will be 63 − x . Now use first, second, and third conditions to form a linear equation.
Step 1:
Let the number of number of winners be xStep 2:
Then the number of participants who do not win ➔ 63 − x [as the total participants is 63]
Total prize money = Rs. 3000
[ number of winners x100 + number of participants who do not win x25]=3000
Number of winners is 19
|
41 videos|48 docs|9 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 2 - Ex 2.2 Linear Equations in One Variable
| 1. What are linear equations in one variable? |  |
| 2. How to solve linear equations in one variable? |  |
| 3. What is the importance of linear equations in one variable? |  |
| 4. Can linear equations in one variable have multiple solutions? |  |
| 5. How can linear equations in one variable be used in everyday life? |  |