NCERT Textbook Exercise 1.1 Solutions: Chapter 1- Real Numbers, Class 10, Mathematics PDF Download
NCERT Mathematics Solutions
Maths Textbook Exercise 1.1 Solutions
(Page 7)
Q.1: Use Euclid’s division algorithm to find the HCF of:
(i) 135 and 225 (ii) 196 and 38220 (iii) 867 and 255
Solution:
(i) We have,
a = bq + r
Applying division lemma to 225 and 135 we obtain,
225 = 135 x 1 + 90
and 135 = 90 x 1 + 45
and 90 = 45 x 2 + 0
Therefore, HCF of 225, 135 = 45
(ii) We have,
a = bq + r
Applying division lemma to 196 and 38220 we obtain,
38220 = 196 x 195 + 0
Therefore, HCF of 196 and 38220 = 196
(iii) We have,
a = bq + r
Applying division lemma to 867 and 255 we obtain,
867 = 255 x 3 + 102
255 = 102 x 2 + 51
102 = 51 x 2 + 0
Therefore, HCF of 867 and 255 is 51.
Q.2: Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or6q + 5, where q is some integer.
Solution:
Let a be any positive number and a = 6. Then, by Euclid’s algorithm,
a = 6q + r (0 ≤ r < 6)
say, r = 0, 1, 2, 3, 4, 5
or, a = 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4 or 6q + 5
Also, 6q + 1 = 2 × 3q + 1 = 2k1 + 1, where k1 is a positive integer,
Similarly, 6q + 3 = (6q + 2) + 1 = 2 (3q + 1) + 1 = 2k2 + 1, where k2 is a positive integer,
and, 6q + 5 = (6q + 4) + 1 = 2 (3q + 2) + 1 = 2k3 + 1, where k3 is a positive integer.
From these we observe that 6q + 1, 6q + 3, 6q + 5 are of the form 2k + 1. So, these numbers are not divisible by 2 and hence, are odd positive integers.
Q.3: An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
To find the maximum number of columns, we have to find HCF of 616 and 32.
Applying Euclid’s algorithm to find the HCF we get,
616 = 32 × 19 + 8
32 = 8 × 4 + 0
Or, the HCF (616, 32) = 8.
Therefore, maximum number of column is 8.
Q.4: Use Euclid’s division lemma to show that the square of any positive integer is either of form 3m or 3m + 1 for some integer m.
Solution:
a = bq + r;
Let a be any positive integer, b = 3 and r = 0, 1, 2 because 0 ≤ r < 3
Then a = 3q + r for some integer q ≥ 0
Therefore, a = 3q + 0 or 3q + 1 or 3q + 2
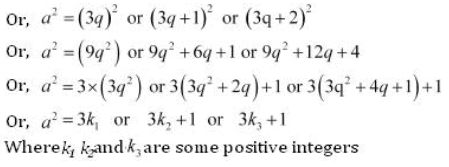
From the above we can say that the square of any positive integer is either of the form 3m or 3m + 1.
Q.5: Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
[Taking hint from the above do it yourselves]
FAQs on NCERT Textbook Exercise 1.1 Solutions: Chapter 1- Real Numbers, Class 10, Mathematics
| 1. What are real numbers and why are they important in mathematics? |  |
| 2. How can we determine if a given number is rational or irrational? |  |
| 3. Can you give an example of a non-repeating and non-terminating decimal number? |  |
| 4. How are real numbers used in practical applications? |  |
| 5. Can all real numbers be represented on a number line? |  |

|
Explore Courses for Class 10 exam
|

|


















