EXERCISE - 1.5
Q.1. Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}. Find
(i) A'
(ii) B'
(iii) (A ∪ C)'
(iv) (A ∪ B)'
(v) (A')'
(vi) (B - C)'
Ans.
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
(i) A' = {5, 6, 7, 8 ,9}
(ii) B' = {1, 3, 5, 7, 9}
(iii) A ∪ C = {1, 2, 3, 4, 5, 6} ∴ (A ∪ C)' = {7, 8, 9}
(iv) A ∪ B = {1, 2, 3, 4, 6, 8} (A ∪ B)' = {5, 7, 9}
(v) (A')' = A = {1, 2, 3, 4}
(vi) B - C = {2, 8} ∴ (B - C)' = {1, 3, 4, 5, 6, 7, 9}
Q.2. If U = {a, b, c, d, e, f, g, h}, find the complements of the following sets
(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g}
(iv) D = {f, g, h, a}
Ans. U = {a, b, c, d, e, f, g, h}
(i) A = {a, b, c} A' = {d, e, f, g, h}
(ii) B = {d, e, f, g} ∴ B' = {a, b, c, h}
(iii) C = {a, c, e, g} ∴ C' = {b, d, f, h}
(iv) D = {f, g, h, a} ∴ D' = {b, c, d, e}
Q.3. Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x : x is an even natural number}
(ii) {x : x is an odd natural number}
(iii) {x : x is a positive multiple of 3}
(iv) {x : x is a prime number}
(v) {x : x is a natural number divisible by 3 and 5}
(vi) {x : x is a perfect square}
(vii) {x : x is perfect cube}
(viii) {x : x + 5 = 8}
(ix) {x : 2x + 5 = 9}
(x) {x : x ≥ 7}
(xi) {x : x ∈ N and 2x + 1 > 10}
Ans. U = N: Set of natural numbers
(i) {x : x is an even natural number}´ = {x : x is an odd natural number}
(ii) {x : x is an odd natural number}´ = {x : x is an even natural number}
(iii) {x : x is a positive multiple of 3}´ = {x : x ∈ N and x is not a multiple of 3}
(iv) {x : x is a prime number}´ = {x : x is a positive composite number and x = 1}
(v) {x : x is a natural number divisible by 3 and 5}´ = {x : x is a natural number that is not divisible by 3 or 5}
(vi) {x : x is a perfect square}´ = {x : x ∈ N and x is not a perfect square}
(vii) {x : x is a perfect cube}´ = {x : x ∈ N and x is not a perfect cube}
(viii) {x : x + 5 = 8}´ = {x : x ∈ N and x ≠ 3}
(ix) {x : 2x + 5 = 9}´ = {x : x ∈ N and x ≠ 2}
(x) {x : x ≥ 7}´ = {x : x ∈ N and x < 7}
(xi) {x : x ∈ N and 2x + 1 > 10}´ = {x : x ∈ N and x ≤ 9/2}
Q.4. If U = {1, 2, 3, 4, 5,6,7,8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that
(i) (A U B)' = A' ∩ B'
(ii) (A ∩ B)' = A' U B'
Ans. It is given that
U = {1, 2, 3, 4, 5,6,7,8, 9}
A = {2, 4, 6, 8}
B = {2, 3, 5, 7}
(i) (A U B)' = {2, 3, 4, 5, 6, 7, 8}' = {1, 9}
A' ∩ B' = {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9} = {1, 9}
Therefore, (A U B)' = A' ∩ B'.
(ii) (A ∩ B)' = {2}' = {1, 3, 4, 5, 6, 7, 8, 9}
A' U B' = {1, 3, 5, 7, 9} U {1, 4, 6, 8, 9} = {1, 3, 4, 5, 6, 7, 8, 9}
Therefore, (A ∩ B)' = A' U B'.
Q.5. Draw appropriate Venn diagrams for each of the following:
(i) (A ∪ B)'
(ii) A' ∩ B'
(iii) (A ∩ B)'
(iv) A' ∪ B'
Ans.
(i) In the diagrams, shaded portion represents (A ∪ B)'
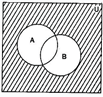
(ii) In the diagrams, shaded portion represents A' ∩ B'
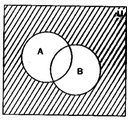
(iii) In the diagrams, shaded portion represents (A ∩ B)'
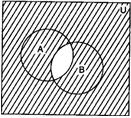
(iv) In the diagrams, shaded portion represents A' ∪ B'
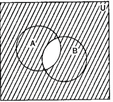
Q.6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60º what is A’?
Ans. Given: U = {x : x is a triangle}
A = {x : x is a triangle and has at least one angle different from 60º}
∴ A' = U – A = {x : x is a triangle and has all angles equal to 60º}
= Set of all equilateral triangles
Q.7. Fill in the blanks to make each of the following a true statement:
(i) A'∪A' = ____
(ii) ϕ'∩A = ____
(iii) A'∩A' = ____
(iv) U'∩A' = ____
Ans.
(i) A'∪ A' = U
(ii) ϕ'∩ A = U ∩ A = A
(iii) A'∩ A' = ϕ
(iv) U'∩ A' = ϕ∩ A = ϕ































