Notes: Applications of Derivatives | Mathematics (Maths) for JEE Main & Advanced PDF Download
Definition
If a quantity ‘y’ changes with a change in some other quantity ‘x’ given the fact that an equation of the form y = f(x) is always satisfied i.e. ‘y’ is a function of ‘x’; then the rate of change of ‘y’ with respect to ‘x’ is given by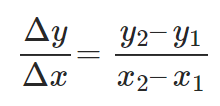
This is also sometimes simply known as the Average Rate of Change.
If the rate of change of a function is to be defined at a specific point i.e. a specific value of ‘x’, it is known as the Instantaneous Rate of Change of the function at that point. From the definition of the derivative of a function at a point, we have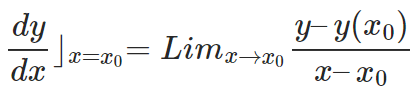
From this, one can conclude that the derivative of a function actually represents the Instantaneous Rate of Change of the function at that point. From the rate of change formula, it represents the case when Δx → 0. Thus, the rate of change of ‘y’ with respect to ‘x’ at x = x0 =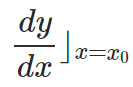
Note: If you plot a quantity ‘y’ as a function of the quantity ‘x’, then the derivative of ‘y’ with respect to ‘x’ represents the SLOPE of the tangent to the curve at that point. (We’ll discuss more tangents in a later section)
If the quantities ‘y’ and ‘x’ are themselves functions of another quantity, say ‘t’; then we can conveniently find the rate of change of y with respect to x from the formula: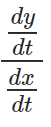
Solved Example
Question 1: A city’s population is modelled as P(t) = 2t2 + 10t + 200 persons(t is the number of years since 2000). What would be the average rate at which the population is changing in 2005?
Solution: For the average rate, we need the information at the beginning point and the endpoint of our domain. Clearly, the beginning point would be the year 2000 corresponding to which, we have t1 = 0 and P(t = 0) = 200. The endpoint: t2 = (2005-2000) = 5 corresponding to which, P(t = 5) = 300. The average rate of change of population in 2005: 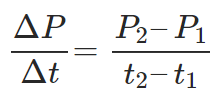
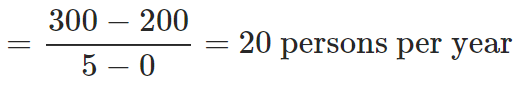
Question 2: Air is being pumped into a spherical balloon at a constant rate such that its radius increases constantly with respect to time according to the equation r(t) = 0.5t + r0(r is in cms and t is in minutes). Find the rate of change of its volume when its radius is 5 cm. Assume that the initial radius of the balloon is r=ocm. Answer with correct units.
Solution: Formula for volume of a sphere of radius r is: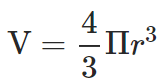
To find dV/dt, we can differentiate the expression for volume to get: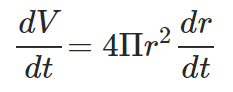
From the given information, we can get; dr/dt = 0.5cm/min. Using this value and r = 5cm in the expression for rate of change of volume, we finally have: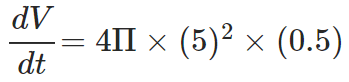
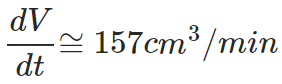
A Physical Example
Velocity and accelerationThis is a very crucial topic in the branch of Mechanics in physics. Given a particle has a position ‘x’ that depends on time ‘t’. Then the rate of change of the particle’s position ‘x’ with time ‘t’ is known as the velocity ‘v’ of the particle. This velocity may or may not depend on time according to the dependence of position on time.
Similarly, if the velocity ‘v’ has a time dependence; then the rate of change of the particle’s velocity ‘v’ with time ‘t’ is known as the acceleration ‘a’ of the particle. Thus, we have:
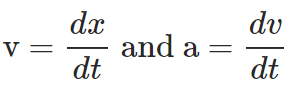
Let us solve a problem on this topic to clarify our concepts!
More Solved Examples for You
Question: A train moves along the railway track in such a way that the distance it covers, starting from the station A, is given by the equation x = 5t2 + t where x is in meters and t is in seconds. What would be the velocity and the acceleration of the train at time t = 25 seconds?
Solution: Given x(t) = 5t2 + t
To find: v(t = 25 sec) and a(t = 25 sec)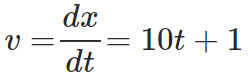
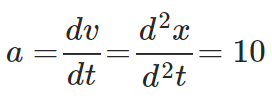
Now putting t = 25sec in the equations, we get v = 251 meters and a = 10 m/s2. Note that in this problem, the acceleration is independent of time. Such motion is said to be uniformly accelerated motion. This concludes the discussion on the Rate of Change of quantities.
Tangent and Normal
- The tangent line to the graph of f at the point P(a, f(a)) is
1. The line on P with slope f'(a) if f'(a) exists ;
2. The line x = a if= ∞.
- In neither (1) nor (2) holds, then the graph of does not have a tangent line at the point P(a, f(a)).
- In case f'(a) exists, then y - f(a) = f'(a) (x - a) is an equation of the tangent line to the graph of f at the point P(a, f(a)).
- The normal line N to the graph of a function f at the point P(a, f(a)) is defined to be the line through P perpendicular to the tangent line.
- It follows that if f'(a)
0 the slope of N is -1/f'(a) and
is an equation of N.
- If f'(a) = 0, then N is the vertical line x = a; and if the tangent line is vertical, then N is the horizontal line y = f(a).
Note :
1. The point P (x1 , y1) will satisfy the equation of the curve & the equation of tangent & normal line.
2. If the tangent at any point P on the curve is parallel to the axis of x then dy/dx = 0 at the point P.
3. If the tangent at any point on the curve is parallel to the axis of y, then dy/dx = ∞ or dx/dy = 0.
4. If the tangent at any point on the curve is equally inclined to both the axes there dy/dx = ± 1.
5. For equation of tangent at (x1, y1), substitute xx1 for x2, yy1 for y2,
for x,
for y and
for xy and keep the constant as such. This method is applicable only for second degree curves, i.e., ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
6. Method to find normal at (x1, y1) of second degree conics ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 The equation of normal at (x1, y1) is
Tangents at the Origin
- If a curve passing through the origin be given by a rational integral algebraic equation, the equation of the tangent (or tangents) at the origin is obtained by equating to zero the terms of the lowest degree in the equation.
e.g., if the equation of a curve be x2 - 4y2 + x4 + 3x3y + 3x2 y2 + y4 = 0, the tangents at the origin are given by x2 - 4y2 = 0 or x + 2y and x - 2y = 0. - In the curve x2 + y2 + ax + by = 0, ax + by = 0, is the equation of the tangent at the origin; and in the curve (x2 + y2)2 = a2 (x2 - y2), x2 - y2 = 0 is the equation of a pair of tangents at the origin.
- If the equation of a curve be x2 + y2 + x3 + 3 x2 y - y3 = 0, the tangents at the origin are given by x2 - y2 = 0 i.e. x + y = 0 and x - y = 0
Angle of intersection
Angle of intersection between two curves is defined as the angle between the two tangents drawn to the two curves at their point of intersection . If the angle between two curves is 90° then they are called ORTHOGONAL curves.
Example 1. Find the equation of tangent to the ellipse 3x2+y2+x+2y = 0 which are perpendicular to the line 4x - 2y = 1.
Sol. Since, tangent is the perpendicular to the line 4x - 2y = 1,
(slope of tangent) × (slope of normal) = –1
The given equation 3x2 + y2 + x + 2y = 0 ....(iii)
Let (x1, y1) be the point of contact of the tangent and the curve
From (i) and (iii), we get
Substituting this in (ii) [since the points lies on the curve] we get,
3x12 + 36x12 + x1 + 12x1 = 0
i.e., 13x1 (3x1 + 1) = 0 ⇒ x1 = 0, –1/3
Using (iv), x1 = 0 ⇒ y1 = 0 and x1 = –1/3 ⇒ y1 = –2
Hence, the points where tangent has slope –1/2 are P(0, 0) and Q(–1/3, –2).
Equation of tangents at P, Q are y = -1/2x i.e. x+2y = 0
i.e., 3x + 6y + 13 = 0 respectively..
Example 2. Find the equation of normal to the curve x + y = xy, where it cuts x-axis.
Sol.
Given curve is x + y = xy .....(i)
at x–axis y = 0, x + 0 = x0 ⇒ x = 1
Point is A(1, 0)
Now to differentiation x + y = xy taking log of both sides
⇒ log(x + y) = y log x
⇒
slope of normal = 1
Equation of normal is,
⇒ y = x – 1
Example 3. At what points on the curve the tangents make equal angles with co-ordintae axes ?
Sol.
Given curve is ....(1)
Differentiating both sides w.r.t.x, then dy/dx = 2x2 + 2
or 2x2 + 2x – x – 1 = 0 or (2x – 1) (x + 1)
(If 2x2 +x + 1 = 0 then x is imaginary)
From (1), for x = 1/2,
Example 4. Show that the curve x = 1 - 3t2, y = t - 3t3 is symmetrical about x-axis and has no real point for x > 1. If the tangent at the point t is inclined at an angle φ to OX. Prove that 3t = tanφ + secφ. If the tangent at P(-2, 2) meets the curve again at Q, prove that the tangents at P and Q are at right angles.
Sol. Given curve is x = 1 - 3t2 ...(1)
& y = t - 3t3 ...(2)
From (1) and (2), y = tx or 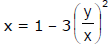 ⇒ x3 = x2 - 3y2
⇒ x3 = x2 - 3y2
Since all powers of y are even, so curve is symmetrical about x-axis.
For x > 1 ⇒ 1 – 3t2 > 1 ⇒ –3t2 > 0 Impossible
From (1) and (2),
...given (3)
Adding (3) and (4) we get, tan ø + secø = 3t
P(–2, 2)
1 – 3t2 = –2 and 2 = t – 3t3 then we get t = –1
Equation of tangent at (–2, 2) is
Therefore the tangent at t = –1 meets the curve again at
Hence the tangents at P and Q are at right angles.
Example 5. Tangent at P(2, 8) on the curve y = x3 meets the curve again at Q. Find coordinates of Q.
Sol. Equation of tangent at (2, 8) is y = 12x - 16
Solving this with y = x3 we get x3 - 12x + 16 = 0
this cubic must give all points of intersection of line and curve y = x3
i.e., point P and Q.
But, since line is tangent at P so x = 2 will be a repeated root of equation x3 -12x + 16 = 0 and another root will be x = h.
Using theory of equations sum of roots ⇒ 2 + 2 + h = 0 ⇒ h = -4
Hence coordinates of Q are (-4, -64)
Example 6. If the normal to the curve x2/3 + y2/3 = a2/3 makes an angle φ with the axis of x, show that its equation is y cosφ - x sinφ = a cos 2φ.
Sol. Given curve is x2/3 + y2/3 = a2/3 ...(1)
Differentiating both sides w.r.t.x, we get
From (1) and (2), y2/3 (1 + tan2Ø) = a2/3 Þ y2/3 = a2/3 cos2Ø
y = a cos3 Ø and x = a sin3 Ø
Therefore equation of normal is y – a cos3 Ø = tan Ø (x – a sin3 Ø)
y cos Ø– a cos4 Ø = x sin Ø – a sin4 Ø
y cosØ– x sin Ø = a (cos4 Ø– sin4 Ø)
= a (cos2 Ø + sin2 Ø) (cos2 Ø- sin2 Ø) = a . 1 . cos 2Ø
Hence y cos Ø– x sin Ø = a cos 2Ø
Example 7. (a) Find y' if x3 + y3 = 6xy.
(b) Find the tangent to the folium of Descartes x3 + y3 = 6xy at the point (3, 3).
(c) At what points on the curve is the tangent line horizontal ?
Sol. (a) Differentiating both sides x3 + y3 = 6xy with respect to x, regarding y as a function of x, and using the Chain Rule on the y3 term and the Product Rule on the 6xy term, we get
3x2 + 3y2y' = 6y + 6xy' or x2 + y2y' = 2y + 2xy'
We now solve for y' :y2y' – 2xy' = 2y – x2
(y2 – 2x)y' = 2y – x2,
(b) When x = y = 3
So, tangent to the folium of Descartes is y – 3 = –1(x – 3) or x + y = 6
(c) The tangent line is horizontal if y' = 0. Using the expression for y' from part (a), we see that y' = 0 when 2y – x2 = 0. Substituting y = 1/2x2 , n the equation of the curve, we get
which simplifies to x6 = 16x3. so either x = 0 or x3 = 16. If x = 161/3 = 24/3, then y = 1/2(28/3) = 25/3. Thus, the tangent is horizontal at (0, 0) and at (24/3, 25/3).
Example 8. In the curve xa yb = ka + b, (a b > 0) prove that the portion of the tangent intercepted between the coordinate axes is divided at its point of contact into segments which are in constant ratio.
Sol. Let P(x1, y1) be the point of contact of the tangent.
Here, xayb = ka + b
∴ a log x + b log y = (a + b) log k.
Solving with y = 0,
Let P divide AB in the ratio λ : 1. Then
P divides AB in the constant ratio b : a.
Example 9. Find the angle between curves y2 = 4x and y = e-x/2
Sol.
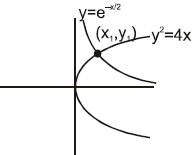
Let the curves intersect at point (x1,y1)
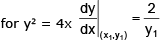
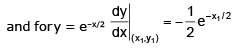
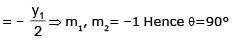
Note: here that we have not actually found the intersection point but geometrically we can see that the curves intersect.
Example 10. Show that the curves y = 2 sin2x and y = cos 2x intersect at π/6. What is their angle of intersection ?
Sol. Given curves are y = 2 sin2 x ...(1)
and y = cos 2x ...(2)
Solving (1) and (2), we get 2 sin2 x = cos 2x
⇒ 1 – cos 2x = cos 2x ⇒ cos2x = 1/2 ⇒ cos π/3 ⇒ 2x = ± π/3
x = ±π/6 are the points of intersection
From (1), dy/dx = 4 sin x cos x = 2 sin 2x = m1 (say)
From (2) dy/dx = -2 sin 2x = m2 (say)
If angle of intersection is θ, then tanθ 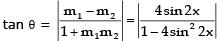
∴ 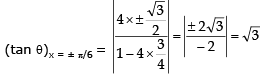
∴ 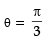
Example 11. Show that the angle between the tangents at any point P and the line joining P to the origin `O' is the same at all points of the curve ln (x2 + y2) = c tan-1 (y/x) where c is constant.
Sol. Let the point P(x, y) on the curve ln (x2 + y2) = c tan-1 (y/x) where c is constant.
Differentiating both sides w.r.t. x, we get
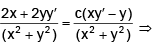
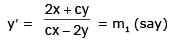
Slope of OP = y/x = m2 (say)
Let the angle between the tangents at P and OP be θ
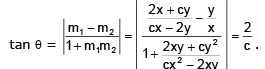
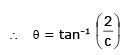 which is independent of x and y.
which is independent of x and y.
Example 12. Show tht the curves 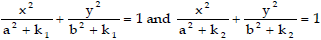 intersect orthogonally.
intersect orthogonally.
Sol.
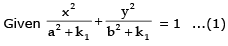
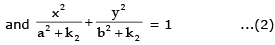
Subtracting (2) from (1), we get 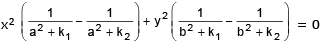
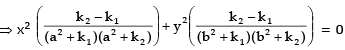
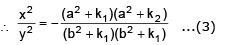

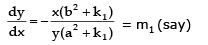
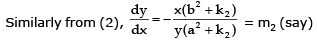
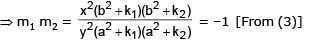
Hence given curves intersect orthogonally.
Example 13. Prove that the curves xy = 4 and x2 + y2 = 8 touch each other.
Sol.
Equation of the given curves are xy = 4 ....(i) and x2 + y2 = 8 ....(ii)
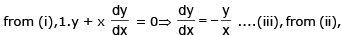
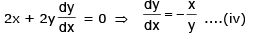
Putting the value fo y from (i) i (ii), we get x2 + 16/x2 = 8 or or x4 + 16 = 8x2
or x4 – 8x2 + 16 = 0 or (x2 – 4)2 = 0 or x2 – 4 = 0 or x2 = 4
from (i) ; when x = 2, y = 2 and when x = –2, y = -2
Hence points of intersection of the two curves are (2, 2) and (–2, –2).
Slope of the tangent to the curve (i) at point (2, 2) ⇒ m1 = -2/2 = -1 ...(from iii)
Slope of tangent to the curve (ii) at point (2, 2) ⇒ m2 = -2/2 = -1....( from iv)
Since m3 = m4, hence the two curves touch each other at (-2, -2). Thus curves (i) and (ii) touch each other.
Slope of tangent to curve (i), 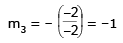
Slope of tangent to curve (ii), 
Since m3 = m4, hence the two curves touch each other at (–2, –2). Thus curves (i) and (ii) touch each other.
Example 14. The gradient of the common tangent to the two curves y = x2 - 5x + 6 & y = x2 + x + 1 is
(A) - 1/3
(B) - 2/3
(C) - 1
(D) - 3
Sol. y = ax + b on solving with both curves and putting D = 0 gives
a2 + 10a + 4b + 1 = 0 and a2 - 2a + 4b - 3 = 0 ⇒ a = - 1/3 & b = 5/9
⇒ 3x + 9y = 5 ; point of contact (7/3, - 2/9) & (- 2/3, 7/9)
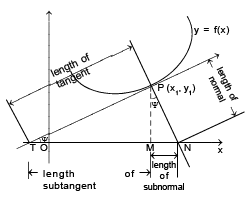
Length of Tangent
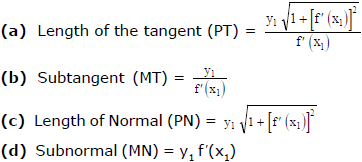
Example 15. What should be the value of n in the equation of curve y = a1 - n. xn, so that the sub-normal may be of constant length ?
Sol. Given curve is y = a1 - n . xn
Taking logarithm of both sides, we get, ln y = (1 - n) ln a + n ln x
Differentiating both sides w.r.tx, we get 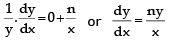 ...(1)
...(1)
Lengths of sub-normal = y dy/dx = y .ny/x ....{from 1}
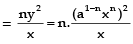
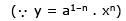
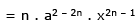
Since lengths of sub-normal is to be constant, so x should not appear in its value i.e., 2n – 1 = 0. n =1/2
Example 16. If the relation between sub-normal SN and sub-tangent ST at any point S on the curve
by2 = (x + a)3 is p(SN) = q(ST)2; then p/q is
(A) 8b/27
(B) b
(C) 1
(D) none of these
Sol.
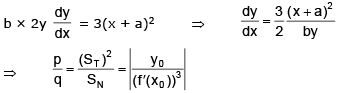
Let a point by (x0, y0) lying on the curve by = (x0 + a)3 ....(i)
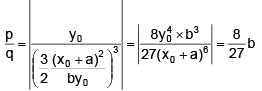 (from equation (i))
(from equation (i))
Example 17. For the curve y = 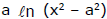 show that sum of lengths of tangent & subtangent at any point is proportional to coordinates of point of tangency.
show that sum of lengths of tangent & subtangent at any point is proportional to coordinates of point of tangency.
Sol.
Let point of tangency be (x1, y1) ⇒ 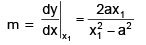
tangent + subtangent = 
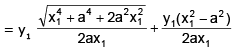
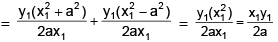 Hence proved.
Hence proved.
Example 18. Show that the segment of the tangent to the curve y = 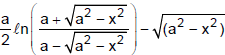 contained between the y-axis and point of tangency has a constant length.
contained between the y-axis and point of tangency has a constant length.
Sol.
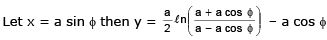
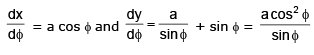
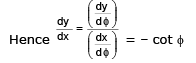
Equation of tangent at ‘ø’ y – a ln cot ø/2 + a cos ø = 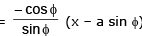
⇒y sin ø – a sinø ln cot ø/2 + a sin ø cos ø - x cosø + a sin ø cos ø
⇒x cos ø+ y sin ø = a sin ø ln cot ø/2
Point on y-axis P ≡ (0, a ln cot ø/2) and point of tangency
Q≡ (a sinø a ln cotø/2 – a cos ø)
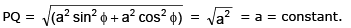
Solving Equations
Example 19. For what values of c does the equation ln x = cx2 have exactly one solution ?
Sol.
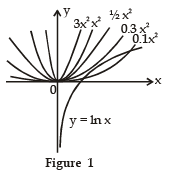
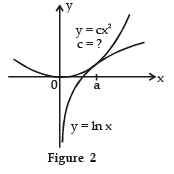
Let's start by graphing y = In x and y = cx2 for various values of c. We know that for c * 0, y = cx2 is a parabola that opens upward if c > 0 and downward if c < 0. Figure 1 shows the parabolas y = cx2 for several positive values of c. Most of them don't intersect y = In x at all and one intersect twice. We have the feeling that there must be a value of c (somewhere between 0.1 and 0.3) for which the curves intersect exactly once, as in Figure 2.
To find that particular value of c, we let 'a' be the x-coordinate of the single point of intersection. In other words, In a = ca2, so 'a' is the unique solution of the given equation. We see from Figure 2 that the curves just touch, so they have a common tangent line when x = a. That means the curves y = In x and y=cx2 have the same slope when x = a. Therefore 1/a = 2ca
Solving the equation In a = ca2 and 1/a = 2ca
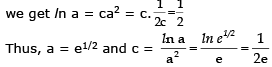
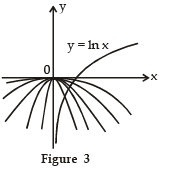
For negative values of c we have the situation illustrated in Figure 3: All parabolas y = cx2 with negative values of c intersect y = In x exactly once. And let's not forget about c = 0: The curve y = 0 x2 = 0 just he x-axis, which intersects y = In x exactly once.
To summarize, the required values of c are c=1/(2e) and c<0
Example 20. The set of values of p for which the equation px2 = ln x possess a single root is
Sol.
for p ≤ 0, there is obvious one solution ; for p > 0 one root
⇒ the curves touch each .
2 px1 = 1/x1 ⇒ x12 = 1/2p ;
Also px12 = ln x1 ⇒ p (1/2p) = ln x1 ⇒ x1 = e1/2
⇒ 2 p = 1/e ⇒ p = 1/2e . Hence p ∈ (- ∝, 0] U {1/2e}
Shortest distance
Shortest distance between two non-intersecting curves always along the common normal (wherever defined)
Example 21. Find the shortest distance between the line y = x - 2 and the parabola y = x2 + 3x + 2.
Sol. Let P(x1, y1) be a point closest to the line y = x - 2 then 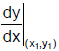 = slope of line
= slope of line
⇒ 2x1 + 3 = 1 ⇒ x1 = - 1 ⇒ y1 = 0 Hence point (-1, 0) is the closest and its perpendicular distance from the
line y = x - 2 will give the shortest distance ⇒ p = 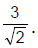
Example 22. Let P be a point on the curve C1: y = 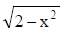 and Q be a point on the curve C2: xy = 9, both P and Q lie in the first quadrant. If 'd' denotes the minimum value between P and Q, find the value of d2.
and Q be a point on the curve C2: xy = 9, both P and Q lie in the first quadrant. If 'd' denotes the minimum value between P and Q, find the value of d2.
Sol. Note that C1 is a semicircle and C2 is a rectangular hyperbola.
PQ will be minimum if the normal at P on the semicircle is also a normal at Q on xy = 9
Let the normal at P be y = mx ....(1) (m > 0) solving it with xy = 9
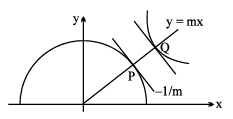
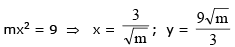
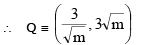
differentiating xy = 9
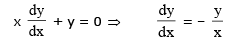
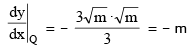
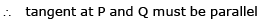
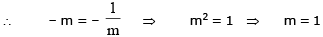
∴ normal at P and Q is y = x
solving P(1, 1) and Q(3, 3)
(PQ)2 = d2 = 4 + 4 = 8
Rate Measurement
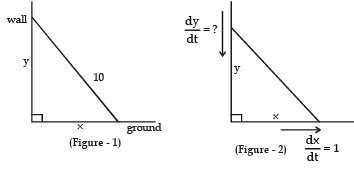
Example 23. A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1 ft/s, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 ft from the wall ?
Sol. We first draw a diagram and label it as in Figure 1. Let x feet be the distance from the bottom of the ladder to the wall and y feet the distance from the top of the ladder to the ground. Note that x and y are both function of t (time). We are given that dx/dt = 1 ft/s and we are asked to find dy/dt when x = 6 ft (see Figure 2). In this problem, the relationship between x and y is given by the Pythagorean Theorem : x2 + y2 = 100
Differentiating each side with respect to t using the Chain Rule, we have 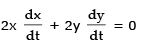
and solving this equation for the desired rate, we obtain 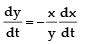
When x = 6, the Pythagorean Theorem gives y = 8 and so, substituting these values and dx/dt = 1,
we have 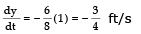
The fact that dy/dt is negative means thatthe distance from the top of the ladder to the ground is decreasing at a rate of 3/4 ft/s In other words, the top of the ladder is sliding down the wall at a rate of 3/4 ft/s .
Example 24. A water tank has the shape of an inverted circular cone with base radius 2 m and height 4 m. If water is being pumped into the tank at a rate of 2 m3/min, find the rate at which the water level is rising when the water is 3 m deep.
Sol.
We first sketch the cone and label it as in Figure. Let V, r, and h be the volume of the water, the radius of the surface, and the height at time t, where t is measured in minutes.
We are given that dV/dt = 2m3/min and we are asked to find dh/dt when h is 3 m. The quantities V and h are related by the equation V = 1/3pr2hBut it is the very useful to express V as a function of h alone.
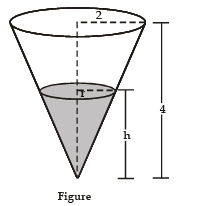
In order to eliminate r, we use the similar triangles in Figure to write 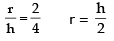 and the expression for V becomes
and the expression for V becomes 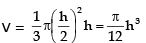
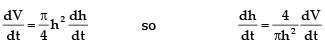
Substituting h = 3 m and dV/dt = 2m3/min, we have 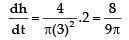
The water level is rising at a rate of 8/(9p) ≈ 0.28 m/min.
Example 25. A man walks along a straight path at the speed of 4 ft/s. A searchlight is located on the ground 20 ft from the path and is kept focused on the man. At what rate is the searchlight rotating when the man is 15 ft from the point on the path closest to the searchlight ?
Sol. We draw Figure and let x be the distance from the man to the point on the path closest to the searchlight. We let θ be the distance from the man to the point on the path closest to the searchlight and the perpendicular to the path.
We are given that dx/dt = 4 ft/s and are asked to find dq/dt when x = 15. The equation that relates
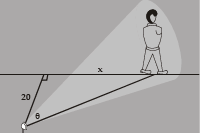
Differentiating each side with respect to t, we get dx/dt = 20sec2 θ dθ/dt
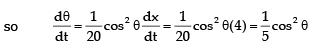
when x = 15, the length of the beam is 25, so cosθ = 4/5
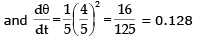
The searchlight is rotating at a rate of 0.128 rad/s.
Example 26. Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45º to each other. If they travel by different roads, find the rate at which they are being separated.
Sol.
Let L and M be the positions of men A and B at any time t,
Let OL = x and LM = y. Then OM = x
given, dx/dt = v; to find dy/dt from ΔLOM,
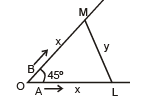
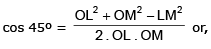
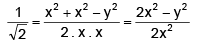
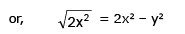
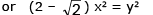
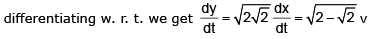
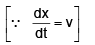
∴ they are being separated from each other at the rate 
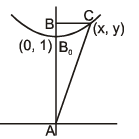
Example 27. A variable triangle ABC in the xy plane has its orthocentre at vertex 'B', a fixed vertex 'A' at the origin & the third vertex 'C' restricted to lie on the parabola y = 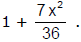 The point B starts at the point (0, 1) at time t = 0 & moves upward along the y axis at a constant velocity of 2 cm/sec. How fast is the area of the triangle increasing when t = 7/2 sec ?
The point B starts at the point (0, 1) at time t = 0 & moves upward along the y axis at a constant velocity of 2 cm/sec. How fast is the area of the triangle increasing when t = 7/2 sec ?
Sol.
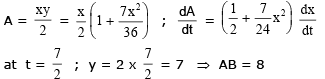
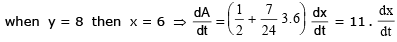

Example 28. Find the approximate value of (1.999)6.
Sol.
Let f(x) = x6. Now, f(x + δx) – f(x) = f'(x) . δx = 6x5 δx
We may write, 1.999 = 2 – 0.001
Taking x = 2 and δx = –0.001, we have f(1.999) – f(2) = 6(2)5 × – 0.001
⇒ f(1.999) = f(2) – 6 × 32 × 0.001 = 64 – 64 × 0.003 = 6
Increasing and Decreasing Functions
A function is basically a relation between input and output such that, each input is related to exactly one output.Functions can increase, decrease or can remain constant for intervals throughout their entire domain. Functions are continuous and differentiable in the given intervals.
An interval in Maths is defined as a continuous/connected portion on the real line. Since it is a “portion of a line”, it basically is a line segment which has two endpoints. So, an interval has two endpoints. Easy to keep track, let’s name our interval and the endpoints and in an interval, assume any two points viz.
x1 and x2 such that x1 < x2. Now, there can be a total of four different cases:
- If f(x1) ≤ f(x2), the function is said to be non-decreasing in l
- If f(x1) ≥ f(x2), the function is said to be non-increasing in l
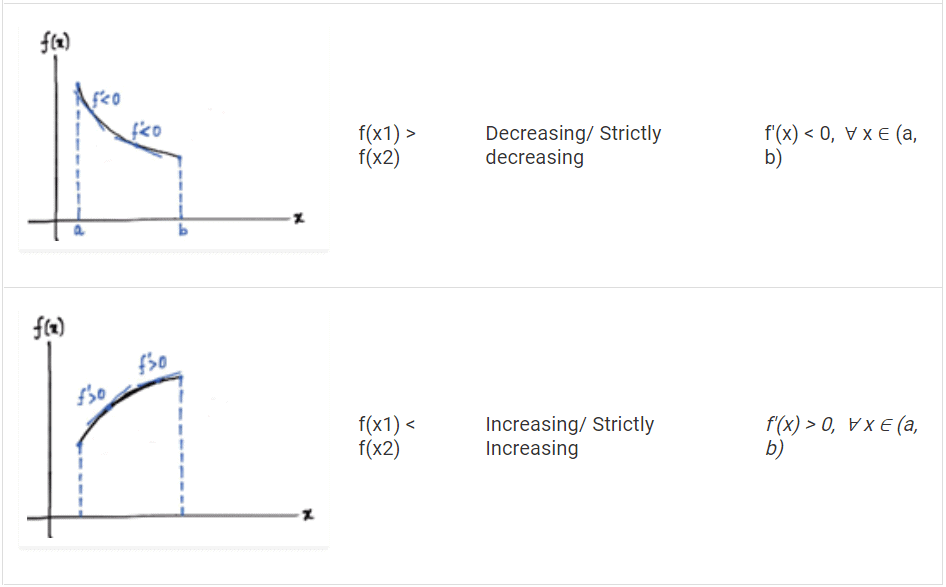
- If f(x1) > f(x2), the function is said to be decreasing (strictly) in l
- If f(x1) < f(x2), the function is said to be increasing (strictly) in l
This increasing or decreasing behaviour of functions is commonly referred to as monotonicity of the function. A monotonic function is defined as any function which follows one of the four cases mentioned above. Monotonic basically has two terms in it. Mono means one and tonic means tone. Together, it means, “in one tone”. When we tell that a function is non-decreasing, does it mean that it is increasing? No. It can also mean the function not varying at all! In other words, function having a constant value for some interval. Never confuse non-decreasing with increasing. That was the definition of increasing and decreasing functions. Let us now see how to know where and in which way the function is behaving.
Test for increasing and decreasing functions
Let us now use derivative of a function to determine the behaviour of a function. To test the monotonicity of a function f, we first calculate it’s derivative f′. There is a small catch here. Before starting the test, make sure that is continuous in the interval [a, b] and differentiable in (a, b). So, for all of the four cases discussed in previous heading, we have tests as:
- For function to be non-decreasing in l, f′(x) ≥ 0,∀ x∈(a, b)
- For function to be non-increasing in l, f′(x) ≤ 0,∀ x∈(a, b)
- For function to be decreasing/strictly decreasing in l, f′(x)< 0,∀ x∈(a, b)
- For function to be increasing/strictly increasing in l,f′(x) > 0,∀ x∈(a, b)<
Let us see examples of each case.

That was increasing and decreasing functions, monotonic functions and monotonicity explained. This concept is particularly very useful for drawing graphs of functions.
Definitions
The function f(x) is called strictly increasing on the open interval (a, b) if for any two points x1 and x2 belonging to the indicated interval and satisfying the inequality x1 < x2 the inequality f(x1) < f(x2) holds true.
The function f(x) is called strictly decreasing on the open interval (a, b) if for any points x1 and x2 belonging to the indicated interval and satisfying the inequality x1 < x2 the inequality f(x1) > f(x2) holds true.
A function f is said to be non-decreasing in an interval I contained in the domain of f
If for all numbers x1, x2 in I.
If f(x1) < f(x2) whenever x1 < x2 for all numbers x1, x2 in I,
then f is said to be strictly increasing in the interval I. Non-increasing and strictly decreasing functions are defined in a similar way. If f is strictly increasing in I, then the graph of f is rising as we traverse it from left to right; if f is strictly decreasing in I, the graph of f is falling in I. Some examples are show in Figure.
If a function f is either non-decreasing in an interval I or non-increasing in I, then f is said to be monotonic in I. Similarly, f is said to be strictly monotonic in I if f is either strictly increasing in I or strictly decreasing in I.
Basic definition test :
The function f(x) is said to be strictly increasing at a point x0 if for a sufficiently small h > 0 the condition (Fig. 1) f(x0 - h) < f(x0) < f(x0 + h) is fulfilled.
The function f(x) is said to be strictly decreasing at a point x0 if for a sufficiently small h > 0 the condition (Fig. 2) f(x0 - h) > f(x0) > f(x0 + h) is fulfilled.
A differentiable function is called increasing in an interval (a, b) if it is increasing at every point within the interval (but not necessarily at the end points). A function decreasing in an interval (a, b) is similarly defined.
Sufficiency Test:
If the derivative function f '(x) in an interval (a , b) is every where positive, then the function f (x) in this interval is Increasing ; If f '(x) is every where negative, then f (x) is Decreasing.
Note : The test (criterion) also holds true when the derivative takes on zero values in the interval (a, b) so long as f (x) does not identically become zero throughout the interval (a, b) or in some interval (a', b') comprising a part of (a, b). The function f (x) would be a constant on such an interval.
If f'(a) = 0 then examine the sign of f'(a+) and f'(a-)
(a) If f'(a+) > 0 and f'(a-) > 0 then strictly increasing
(b) If f'(a+) < 0 and f'(a-) < 0 then strictly decreasing
Note : If a function is invertible it has to be either increasing or decreasing.
If a function is continuous in the intervals in which it rises and falls may be separated by points at which its derivative is zero or it fails to exist.
Critical Point
A critical point of a function f is a number c in the domain of f such the either f'(c) = 0 or f'(c) does not exist.
Ex.1 Find the critical points of f(x) = x3/5 (4 - x).
Sol.
Therefore, f'(x) = 0 if 12 – 8x = 0, that is, x = 3/2. and f'(x) does not exist when x = 0.
Thus, the critical points are 3/2 and 0.
Ex.2 Find the critical numbers for the function
Sol.
The derivative is not defined at x = 2, but f is not defined at 2 either, so x = 2 is not a critical number. The actual critical numbers are found by solving f'(x) = 0 :
= 0
x = 3 This is the only critical number since ex > 0.
Ex.3 Find all possible values of the parameter ' b ' for which the function,
f (x) = sin 2 x - 8 (b + 2) cos x - (4 b2 + 16 b + 6) x
is monotonic decreasing throughout the number line and has no critical points.
Sol. f ' (x) = 2 cos 2 x + 8 (b + 2) sin x - (4 b2 + 16 b + 6)
= 2 (1 - 2 sin2 x) + 8 (b + 2) sin x - (4 b2 + 16 b + 6)
= - 4 [ sin2 x - 2 (b + 2) sin x + (b2 + 4 b + 1) ]
for monotonic decreasing and no critical points
Now, D = 4 (b + 2)2 - 4 (b2 + 4 b + 1) = 4 [3] = 12 which is always positive .
Now let sin x = y ; y ε [- 1 , 1]
g (y) = y2 - 2 (b + 2) y + (b2 + 4 b + 1)
we have to find those values of ' b ' for which g (y) > 0 for all y ε (- 1 , 1)
Conditions are
First condition gives 1 + 2 (b + 2) + b2 + 4 b + 1 > 0
b2 + 6 b + 6 > 0 .....(1) & < -1 or b < - 3 .....(2)
Ex.4 If where 0 < x < 1, then
Sol. Put x = π/6 & π/3 and observe the behavior of f(x) & g(x) . Alternatively
consider = 2 (1 - cos x) - x sin x
consider x - 2 sin x + x cos x
= 2x cos2x - 4 sin x cos x
Ex.5 Find possible values of a such that f(x) = e2x - (a + 1) ex + 2x is strictly increasing for x ε R.
Sol. f(x) = e2x - (a + 1) ex + 2x
f '(x) = 2e2x - (a + 1) ex + 2
Now, f(x) = e2x - (a + 1) ex + 2x ≥ 0 for x ∈R
Aliter : 2e2x – (a + 1) ex + 2 ≥ 0 for x ∈R
putting ex = t ; t ∈ (0,∝)
2t2 – (a + 1) t + 2 ≥ 0 for t∈ (0, ∝)
Hence either
(i) D ≤ 3 ⇒ (a + 1)2 – 4 ≤ 0 ⇒ (a + 5) (a – 3) ≤ 0 ⇒ a ∈ [–5, 3]
(ii) both roots are negative
D ≥ 0 & -b/2a < 0 & f(0) ≥ 0
Taking union of (i) and (ii), we get a ∈ (–∝, 3].
Ex. 6 Prove that the function f(x) = is strictly decreasing in (e, ∞). Hence, Prove that 303202 < 202303.
Sol.
We have f(x) = ,x > 0,
⇒ f(x) strictly decreases in (e,∝) Thus, we have f(303) < f(202)
i.e . 202 ln (303) < 303 ln (202)
⇒ 303202 < 202303 which is the desired result.
Ex.7 Let f(x) = x3 + 2x2 + x + 5. Show that f(x) has only one real root a such that [α] = -3.
Sol. We have f(x) = x3 + 2x2 + x + 5, x ∈ R and f '(x) = 3x2 + 4x + 1 = (x + 1) (3x + 1), x ∈ R
Drawing the number line for f'(x), we have f(x) strictly increases in (–∝, –1) strictly decreases in (–1, –1/3) strictly increases in (–1/3, ∝)
Also, we have f(–1) = –1 + 2 – 1 + 5 = 5 and
The graph of f(x) (see fig.) shows that f(x) cuts the X-axis only once.
Now, we havef(–3) = – 27 + 12 – 3 + 5 = – 13 and f(–2) = –8 + 8 – 2 + 5 = 3.
Which are of opposite signs. This proves that the curve cuts the X-axis somewhere between –2 and –3.
⇒ f(x) = 0 has a root α lying between – 2 and –3. Hence [α] = –3
Ex.8 Find the number of real roots of the equation = c where b1 < b2 < ..... <bn.
Sol.
Consider the function f(x) =
= f(x) strictly decreases in (–α, b1) U (b1,b2) U ... U (bn – 1, bn)
Now, we have
The plot of the curve y = f(x) is shown alongside.
Ex.9 If f: R → R and f is a polynomial with f(x) = 0 has real and distinct roots, show that the equation, [ f ' (x) ]2 - f(x) . f '' (x) = 0 cannot have real roots.
Sol. Let f(x) = c (x - x1) (x - x2) ...... (x - xn)
Again Let
⇒ h ' (x) < 0 ⇒ f(x) . f '' (x) - [f ' (x)]2 < 0
Alternatively : a function f(x) satisfying the equation [f ' (x)]2 - f(x) . f '' (x) = 0 is which can't have any root.
Intervals of Monotonicity
Ex.10 Find the intervals of monotonocity of the following functions :
(a) f(x) =
(b) f(x) =
(c) f(x) =
Sol.
(a) We have
Now, from the sign scheme for f'(x), we have ⇒ f(x) strictly increases i (-∞, 0)
strictly decreases in (0, 1) ; strictly increases in (1, 2) ; strictly decreases in (2, ∞)
Ans. : Increases in (-∞, 0), (1, 2); Decreases in (0, 1), (2, ∞)
(b) We have f(x)=2x2 – ln |x| and f '(x) = 4x – 1/x =
Now, from the sign scheme for f'(x), we have ⇒ f(x) strictly decreases in (-∞, -1/2)
strictly increases in (-1/2, 0) ; strictly decreases in (0, 1/2) ; strictly increases in (-1/2, ∞)
Ans. :
(c)
⇒ f(x) strictly decreases in (-∞, -3) ; strictly increases in (-3, 3) ; strictly decreases in (3, ∞).
Ans : Increases in (-3, 3) ; Decreases in (-∞, -3), (3, ∞)
Ex.11 A function f (x) is given by the equation , x2 f ' (x) + 2 x f (x) - x + 1 = 0 (x 0). If f (1) = 0 , then find the intervals of monotonocity of f.
Sol.
wherey = f (x)
Ans. : I in (- ∝, 0) U (1, ∝) ; D in (0, 1)
Operations on Monotonous Functions
I. (a) Negative : If f is an increasing function then its negative i.e. h = –f is a decreasing function.
By derivative h'(x) = –f'(x), f'(x) > 0 ∴h'(x) < 0
⇒ h is a decreasing function
In short – (an increasing function) = a decreasing function i.e. –I = D Similarly –D = I
(b) Reciprocal : Reciprocal of an increasing function is a decreasing function
II.(a) Sum : If f is an increasing function and g is also an increasing function their h = f + g is an increasing function.
By derivative
h'(x) = f'(x) + g'(x) f & g are increasing function, ⇒ f '(x) & g'(x) are positive ⇒ f '(x) + g'(x) is positive ⇒ f(x) + g(x) increases
In short, An increasing function + An increasing function = An increasing function
i.e. (i) I + I = I (ii) I + D = can’t say (iii) D + D = D
(b) Difference : Monotonocity of the difference of two function can be predicted using I(a) and II(a)
I - I = I + (-I) = I + D = can't say
I - D = I + (-D) = I + I = increasing
D - I = D + (-I) = D + D = decreasing
D - D = D + (-D) = D + I = can't say
III. (a) Product : Consider h = f × g
Case I : Both the function involved in the product i.e. f & g are positive
If f & g both are increasing function then h = f × g is also an increasing function.
In short I × I = I, I × D = can't say, D × D = D.
Case II : If any of the function takes negative values then we can predict the monotonocity by using I(a) & case I of III(a). If a function f is increasing & takes negative values & another function g is decreasing & takes positive values.
then h(x) = f(x) × g(x) = (-f(x)) × g(x) = - = increasing
(b) Division : Monotonocity of division of two functions can be predicted by using I(b) & III(a).
= I × I = I (assuming that both the functions I & D take positive values).
IV. Composition :
(I) I (I)= I
(II) I(D) = D
(III) D (I) = D
(IV) D(D) = I
Let h(x) = D(D(x)) x increases ⇒ D(x) decreases ⇒ D(D(x)) increases
Inequalities
General Approach to prove Inequalities :
To prove f(x) ≥ g(x) for x ≥ a, we Assume h(x) = f(x) – g(x)
Find h'(x) = f'(x) – g'(x)
If h'(x) ≥ 0 Apply increasing function h on x ≥ a to get h(x) ≥ h(a).
If h(a) ≥ 0 then h(x) ≥ 0 for x ≥ a i.e. then given inequality is true.
If h'(x) ≤ 0 Apply decreasing function h on x ≥ a to get h(x) ≤ h(a).
If h(a) ≤ 0 then h(x) ≤ 0 for x ≥ a i.e. the given inequality is false
Note : If the sign of h'(x) is not obvious then to determine its sign assume g(x) = h'(x) & apply the above procedure on g(x).
Ex.12 Prove that, 2 x sec x + x > 3 tan x for 0 < x <  /2 .
/2 .
Sol. f(x) = 2x sec x + x - 3 tan x
f ' (x) = 2 sec x + 2x sec x tan x + 1 - 3 sec2x = sec2 x [2 cos x + 2x sin x + cos2x - 3]
Consider g(x) = 2 cos x + 2x sin x + cos2x - 3
g ' (x) = - 2 sin x + 2x cos x + 2 sin x - 2 sin x cos x = 2 cos x (x - sin x) > 0 for x ε (0, /2)
Ex.13 Prove that tan x > x + for all x ε
.
Sol.
...(1)
Clearly, f(x) is defined at all x ∈ (0, π/2).
Now, f'(x) = sec2x – 1 x– x2 ...(2)
f''(x) = 2 sec2 x . tan x – 2x...(3)
f'''(x) = 2 sec4x + 4 sec2 x. tan2 x – 2 = 2 (1 + tan2x)2 + 4 sec2x . tan2 x – 2
= 2tan4x + 4 tan2x + 4 sec2x . tan2x > 0 for all x ∈ (0, π/2)
⇒ f'''(x) > 0 in the interval (0, p/2) ⇒ f''(x) is monotonic increasing in (0, π/2)
f''(x) > f''(0) when x ∈ (0, π/2).
But from (3), f''(0) = 0. Thus, f''(x) > 0 for all x ∈ (0, π/2)
∴f'(x) is monotonic increasing in (0, π/2)
∴f'(x) > f'(0) when x ∈ (0, π/2)
But from (2), f'(0) = 1 – 1 – 0 = 0.
Thus, f'(x) > 0 for all x ∈ (0, p/2)
∴f(x) is monotonic increasing in (0, π/2)
∴f(x) > f(0) when x ∈ (0, π/2)
But from (1), f(0) = 0.
Thus, f(x) > 0 for all x ∈ (0, π/2)
∴
Ex.14 Show that
Sol.
or
or
Since, f(x) is increasing for, x ≥ 0 ⇒ f(x) ≥ f(0)
⇒
Ex.15 Examine which is greater sin x tan x or x2. Hence evaluate
Sol. Let f(x) = sin x . tan x - x2
f '(x) = cos x . tan x + sin x . sec2x - 2x = sin x + sin x sec2 x - 2x
⇒ f ''(x) = cos x + cos x sec2 x + 2 sec2 x sin x tan x - 2
⇒ f ''(x) = (cos x + sec x - 2) + 2 sec2 x sin x tan x
Now cos x + sec x – 2 = and 2 sec2 x tan x . sin x > 0 because
⇒ f''(x) > 0 ⇒ f'(x) is M.I.
Hence f'(x) > f'(0)
⇒ f'(x) > 0 ⇒ f(x) is M.I. ⇒ f(x) > 0 ⇒ sin x tan x – x2 > 0
Hence sin x tan x – x2
Ex.16 Prove :
Sol. Consider the function f(x) = cot (x/2) – 1 – cot x, x ∈ (0, p)
⇒ f(x) strictly decreases in (0, π/2) strictly increases in (π/2, π)
⇒ f(x) has least value at x = π/2 ⇒ f(x) ≥ f(π/2) = 0
which proves the desired result.
Ex.17 Prove that Hence, show that the function f(x)=
strictly increases in (0, ∞).
Sol.
Consider the fucntion g(x) =
⇒ g(x) strictly decreases in (0, ∝) ⇒
which gives the desired result
Now, we have f(x)
[using result (1)] ⇒ f(x) strictly increases in (0, ∝)
Ex.18 Prove that
Sol.
Let f(x) = sin x tan x – x2 ⇒ f'(x) = sin x sec2x + sin x – 2x
⇒ f''(x) = 2 sin x sec2 x tan x + cos x – 2 + sec x
= 2 sin x tan x sec2 x + (cos x + sec x – 2)
⇒ f'(x) is an increasing function.
⇒ f'(x) > f'(0) ⇒ sin x sec2 x + sin x – 2x > 0
⇒ f(x) is an increasing function ⇒ f(x) > f(0) sin x tan x – x2 > 0 ⇒ sin x tan x > x2
Ex.19 Prove that sin 1 > cos (sin 1). Also show that the equation sin (cos (sin x)) = cos (sin (cos x)) has only one solution in
Sol. sin 1 > cos (sin 1) if
...(1)
Hence (1) is true ⇒ sin 1 > cos (sin 1).
Now let f(x) = sin (cos (sin x)) – cos (sin (cos x))
and f(0) = sin 1 – cos (sin 1) > 0
Since f(0) is positive and f(x) = 0 has one solution in
Ex.20 Using calculus establish the inequality, (xb + yb)1/b < (xa + ya)1/a , where x > 0 , y > 0 and b>a>0.
Sol. (xb + yb)1/b < (xa + ya)1/a
or T P T (tb + 1)a/b < ta + 1
Let f (t) = (tb + 1)a/b - ta - 1
Hence f'(t) < 0 i.e. f (t) is decreasing function
So f (t) < f (0) but f (0) = 0 ⇒ (tb + 1)a/b < ta + 1 Hence proved
Ex.21 Prove that the function f(x) = 2x3 + 21x2 - 60x + 41 is strictly positive in the interval (-∞, 1).
Sol.
f(x) = –2x3 + 21x2 – 60x + 41
f'(x) = –6x2 + 42x – 60 = – 6(x2 – 7x + 10) = –6(x – 5) (x – 2)
x ∈ (2, 5) ⇒ f'(x) > 0, i.e., f(x) is m.i.
and x Ï (2, 5) ⇒ f'(x) < 0 i.e., f(x) is m.d. ∴ x ∈ (–∝, 1) ⇒ f(x) is m.d.
When x ∈ (–∝, 1), x < 1; so, f(x) > f(1).
But f(1) = –2 + 21 – 60 + 41 = 0.
∴ x ∈ (–∝, 1) ⇒ f(x) > f(1) = 0
∴ f(x) is strictly positive in the interval (–∝, 1).
Rolle's Theorem
Let f be a function that satisfies the following three hypotheses :
1. f is continuous on the closed interval [a, b].
2. f is differentiable on the open interval (a, b).
3. f(a) = f(b)
Then there is a number c in (a, b) such that f'(c) = 0
Before given the proof let's take a look at the graphs of some typical functions that satisfy the three hypotheses. Figure 1 shows the graph of four such functions. In each case it appears that there is atleast one point (c, f(c)) on the graph where the tangent is horizontal and therefore f'(c) = 0. Thus, Rolle's Theorem is plausible.
Proof : There are three cases :
Case I : f(x) = k, a constant. Then f'(x) = 0, so the number c can taken to be any number in (a, b).
Case II : f(x) > f(a) for some x in (a, b) [as in Figure 1(b) or (c)]
By the Extreme Value Theorem (which we can apply by hypothesis 1), f has a maximum value somewhere in [a, b]. Since f(a) = f(b), it must attain this maximum value at a number c in the open interval (a, b). Then f has a local maximum at c and, by hypothesis 2, f is differentiable at c. Therefore, f'(c) = 0 by Fermat's Theorem.
Case III : f(x) < f(a) for some x in (a, b) [as in Figure 1(c) or (d)]
By the Extreme Value Theorem, f has minimum value in [a, b] and, since f(a) = f(b), it attains this minimum value at a number c in (a, b). Again f'(c) = 0 by Fermat's Theorem.
Ex.22 Prove that the equation x3 + x - 1 = 0 has exactly one real root.
Sol. First we use the Intermediate Value Theorem to show that a root exists. Let f(x) = x3 + x - 1. Then f(0) = -1 < 0 and f(1) = 1 > 0. Since f is a polynomial, it is continuous, so the Intermediate Value Theorem states that there is a number c between 0 and 1 such that f(c) = 0. Thus, the given equation has a root.
To show that the equation has no other real root, we use Rolle's Theorem and argue by contradiction. Suppose that it had two roots a and b. Then f(a) = 0 = f(b) and, since f is a polynomial, it is differentiable on (a, b) and continuous on [a, b]. Thus, by Rolle's Theorem, there is a number c between a and b such that f'(c) = 0. But for all x
(since x2 ≥ 0) so f'(x) can never be 0. This gives a contradiction. Therefore, the equation can't have two real roots.
Ex.23 Let f (x) & g (x) be differentiable for such that f (0) = 2, g (0) = 0, f (1) = 6 . Let there exist a real number c in [0, 1] such that f ' (c) = 2 g ' (c) , then the value of g (1)
Sol. Consider φ(x) = f (x) - 2 g (x) defined on [0, 1] since f (x) and g(x) are differentiable for therefore f (x) is differentiable on (0, 1) and continuous on [0, 1]
ø(0) = ø (0) - 2 g (0) = 2 - 0 = 2 ø (1) = f (1) - 2 g (1) = 6 - 2 g (1)
Now f '(x) = f '(x) - 2 g '(x) ⇒ f '(c) = f '(c) - 2 g '(x) = 0 (given)
⇒ f (x) satisfies Rolle's theorem on [0, 1] ∴ ø (0) =ø(1) ⇒ 2 - 6 - 2 g (1) ⇒ g (1) = 2
Our main use of Rolle's Theorem is in proving the following important theorem, which was first stated by another French mathematician, Joseph-Louis Lagrange.
Ex.24 If f(x) is continuous in [a, b] and differentiable in (a, b), prove that there is atleast one c ε(a, b), such that .
Sol. Let us consider a function, h(x) = f(x) - f(a) + A (x3 - a3)
Where A is obtained from the relation h(b) = 0.
So that, 0 = h(b) = f(b) - f(a) + A(b3 - a3) ...(i)
also, h(a) = 0
Since, (1) h(x) is continuous in [a, b] (2) h(x) is differentiable in (a, b) and (3) h(a) = 0 = h(b)
hence, all the three condition of Rolle's theorem. Then there must exists a'c' ε (a, b) such that f'(c) = 0.
⇒ f'(c) + A (3c2) = 0 or
The Mean Value Theorem
Let f be a function that satisfies the following hypotheses :
1. f is continuous on the closed interval [a, b].
2. f is differentiable on the open interval (a, b).
Then there is a number c in (a, b) such that
Before proving this theorem, we can see that it is reasonable by interpreting it geometrically. Figures (a) and (b) show that points A(a, f(a)) and B(b(b, f(b)) on the graphs of two differentiable functions. The slope of the secant line AB is
which is the same expression as on the roght side od eq. 1. Since f'(c) is the slope of the tangent line at the point (c, f(c)), the Mean Value Theorem, in the form given by Equation 1, says that there is at least one point P(c, f(c)) on the graph where the slope of the tangent line is the same as the slope of the secant line AB. In other words, there is a point P where the tangent line is parallel to the secant line AB.
Proof We apply Rolle’s Theorem to a new function h defined as the difference between f and the function whose graph is the secant line AB. Using Equation 3, we see that the equation of the line AB can be written as
First we must verify that h satisfies the three hypotheses of Rolle's Theorem.
1. The function h is continuous on [a, b] because it is the sum of f and a first-degree polynomial, both of which are continuous.
2. The function h is differentiable on (a, b) because both f and the first-degree polynomial are differentiable. In fact we can compute h' directly from Equation 4 :
(Note that f(a) and [f(b) - f(a)]/(b - a) are constants.)
3.
h(a) = f(a) – f(a) -
h(b) = f(b) – f(a) -
Since h satisfies the hypotheses of Rolle's Theorem, that theorem says there is a number c in (a, b) such that h'(c) = 0. Therefore
Ex.25 To illustrate the Mean Value Theorem with a specific function, let's consider f(x) = x3 - x, a= 0, b = 2. since f is a polynomial, it is continuous and differentiable for x, so it is certainly continuous on [0, 2] and differentiable on (0, 2) such that f(2) - f(0) = f'(c)(2 - 0)
Sol.
Ex.26 If for all x and f(0) = 0, show that 0.4 < f(2) < 2
Sol.
...(1)
f'(x) > 0 for all x [∴1 + x2 > 0]
Also given f(0) = 0 ...(2)
From (1), it follows that f(x) is differentiable at all x, therefore f(x) is also continuous at all x
∴ by Lagrange’s mean value theorem in [0, 2]
Now 0 < c < 2
...(4)
From (3), (4) and (5) it follows that 0.4 < f(2) < 2.
Curve Sketching
The following checklist is intended as a guide to sketching a curve y = f(x). Not every item is relevant to every function. (For instance, a given curve might not have an asymptote or possess symmetry.) But the guidelines provide all the information you need to make a sketch that displays the most important aspects of the function.
I. Domain It's often useful to start by determining the domain D of f, that is, the set of values of x for which f(x) is defined.
II. Intercepts The y-intercept is f(0) and this tells us where the curve intersect the y-axis. To find the x-intercepts, we set y = 0 and solve for x. (You can omit this step if the equation is difficult to solve.)
III. Symmetry
(a) If f(-x) = f(x) for all x in D, that is, the equation of the curve is unchanged when x is replaced by -x, then f is an even function and the curve is symmetric about the y-axis. This means that out work is cut in half. If we know what the curve looks like for then we need only reflect about the y-axis to obtain the complete curve [see Figure (a)]. Here are some examples : y = x2, y = x4, y = |x|, and y = cos x.
(b) If f(-x) = -f(x) for all x in D, then f is an odd function and the curve is symmetric about the origin. Again we can obtain the complete curve if we know what it looks like for [Rotate 180º about the origin; see Figure (b).] Some simple examples of odd functions are y = x, y = x3, y = x5, and y = sin x.
Figure
(c) If f(x + p) = f(x) for all x in D, where p is positive constant, then f is called a periodic function and the smallest such number p is called the period. For instance, y = sin x has period 2 and y = tan x has period
. If we know what the graph looks like in an interval of length p, then we can use translation to sketch the entire graph (see Figure ).
IV. Asypmtotes
(a) Horizontal Asymptotes. If either f(x) = L or
f(x) = L, then the line y = L is a horizontal asymptote of the curve y = f(x). If it turns out that
f(x) = ∞ (or - ∞), then we do not have an asymptote to the right, but that is still useful information for sketching the curve.
(b) Vertical Asymptotes. The line x = a is a vertical asymptote if at least one of the following statements is true :
(For rational functions you can locate the vertical asymptotes by equating the denominator to 0 after canceling any common factors. But for other functions this method does not apply.) Furthermore, in sketching the curve it is very useful to know exactly which of the statements in (ii) is true. If f(a) is not defined but a is an endpoint of the domain of f, then you should compute or
f(x), whether or not this limit is infinite,
V. Interval of Increase / Decrease Use the I/D Test. Compute f'(x) and find the intervals on which f'(x) is positive (f is increasing) and the intervals on which f'(x) is negative (f is decreasing).
VI. Local Maximum and Minimum Value Find the critical numbers of f [the number c where f'(c) = 0 or f'(c) does not exist]. Then use the First Derivative Test. If f' changes from positive to negative at a critical number c, then f(c) is a local maximum. If f' changes from negative to positive at c, then f(c) is a local minimum. Although it is usually preferable to use the First Derivative Test, you can use the Second Derivative Test if c is a critical number such that f''(c) 0. Then f''(c) > 0 implies that f(c) is a local minimum, whereas f''(c) < 0 implies that f(c) is a local maximum.
VII. Concavity and Points of Inflection Compute f'(x) and use the Concavity Test. The curve is concave upward where f''(x) > 0 and concave downward where f''(x) < 0. Inflection points occur where the direction of concavity changes.
VIII. Sketch the Curve Using the information in items A - G, draw the graph. Sketch the asymptotes as dashed lines, Plot the intercepts, maximum and minimum points, and inflection points. Then make the curve pass through these points, rising and falling according to E, with concavity according to G, and approaching the asymptotes. If additional accuracy is desired near any point, you can compute the value of the derivative there. The tangent indicates the direction in which the curve proceeds.
Ex.27 Use the guidelines to sketch the curve y = .
Sol.
I. The domain is {x|x2 – 1 ≠ 0} = {x | x ≠ ± 1} = (– ∝ , – 1) U (–1, 1) U (1. ∝)
II. The x-and y-intercepts are both 0.
III. Since f(-x) = f(x), the function f is even. The curve is symmetric about the y-axis.
IV. Therefore, the line y = 2 is a horizontal asymptote.
Since the Denominator is 0 when x = ±1, we compute the following limits :
Therefore, the lines x = 1 and x = -1 are vertical asymptotes. This information about limits and asymptotes enables us to draw the preliminary sketch in Figure, showing the parts of the curve near the aymptotes.
V.
Since f'(x) > 0 when x < 0 (x ≠ -1) and f'(x) < 0 when x > 0 when x > 0 (x ≠ 1), f is increasing on (-∝, -1) and (-1, 0) and decreasing on (0, 1) and (1, ∝).
VI. The only critical number is x = 0. Since f' changes from positive to negative at 0, f(0) = 0 is local maximum by the First Derivative Test.
VII.
Since 12x2 + 4 > 0 for all x, we have
f''(x) > 0 ⇔ x2 – 1 > 0 ⇔ |x| > 1
VIII. Using the information in V – VI, we finish the sketch in Figure.
Ex.28 Sketch the graph of f(x) = .
Sol.
I. Domain = {x|x + 1 > 0} = {x|x > –1} = (–1, ∝)
II. The x- and y-intercepts are both 0.
III. Symmetry : None
IV. Since there is no horizontal asymptote. Since
and f(x) is always positive, we have
and so the line x = –1 is a vertical asymptote.
V.
We see that f'(x) = 0 when x = 0 (notice that - 4/3 is not in the domain of f), so the only critical number is 0. Since f'(x) < 0 when -1 < x < 0 and f'(x) > 0 when x> 0, f is decreasing on (-1, 0) and increasing on (0, ∝)
VI. Since f'(0) = 0and f' changes from negative to positive at 0, f(0) = 0 is a local (and absolute) minimum by the first derivative.
VII.
Note that the denominator is always positive. The numerator is the quadratic 3x2 + 8x + 8, which is always positive because its discriminant is b2 – 4ac = –32, which is negative, and the coefficient of x2 is positive. Thus, f''(x) > 0 for all x in the domain of f, which means that f is concave upward on (-1, to) and there is no point of inflection.
VIII. The curve is sketched in Figure.
Ex.29 Sketch the graph of f(x) = xex
Sol. I. The domain is R.
II. The x- and y-intercepts are both 0.
III. Symmetry : None
IV. Because both x and ex become large as x → ∝, we have however, ex → 0 and so we have an indeterminate product that requires the use of L’Hospital’s Rule :
Thus, the x-axis is horizontal asymptote.
V
VI. Because f'(–1) = 0 and f changes from negative to positive at x = –1, f(–1) = –e–1 is a local (and absolute) minimum.
VII. f''(x) = (x + 1)ex + ex = (x + 2)ex Since f''(x) > 0 if x > –2 and f''(x) < 0 if x < –2, f is concave upward on (–2, ∝) and concave downward on (– ∝, – 2). The inflection points in (–2, –2e–2)
VIII. We use this information to sketch the curve in Figure.
Ex.30 Sketch the graph of the function f(x) = x2/3(6 - x)1/3.
Sol. You can use the differentiation rules to check that the first two derivatives are
Since f'(x) = 0 when x = 4 and f'(x) does not exist when x = 0 or x = 6, the critical numbers are 0, 4 and 6.To find the local extreme values we use the First Derivative Test. Since f' changes from negative to positive at 0, f(0) = 0 is a local minimum. Since f' changes from positive to negative at 4, f(4) = 25/3 is a local maximum. The sign of f' does not change at 6, so there is no minimum or maximum there Looking at the expression for f''(x) and noting that x4/3 > 0 for all x, we have f''(x) < 0 for x < 0 and for 0 < x < 6 and f''(x) > 0 for x > 6. So f is concave downward on (-x, 0) and (0, 6) and concave upward on (6, x), and the only inflection point is (6, 0). The graph is sketched in Figure. Note that the curve has vertical tangents at (0, 0) and (6, 0) because |f'(x)| → ∝ as x → 0 and as x→ 6
Ex.31 Plot the following curves :
Sol.
(a) We have whose domain is x ∈ R, and
y' = x2 – 3x + 2 = (x – 1) (x – 2) > 0 for x ∈ (–∝, 1) U (2, ∝) < 0 for x ∈ (1, 2)
⇒ y strictly increases in (–∝, 1) strictly decreases in (1, 2) ; strictly increases in (2, ∝)
Now we have
y (–∝) –∝, y(∝) = ∝
The curve cuts the Y-axis at (0, 6).
The cure cuts the –ve X-axis somewhere between –1and –2, since
The plot of the curve is shown along side.
(b) We have y = x/ln x Whose domain is x ∈ (0, ∝) ~ {1}, and
⇒ y strictly decreases in (0, 1) U (1, e) ; strictly increases in (e, ∝)
The plot of the curve is shown alongside.
(c) We have y = x ln x whose domain is x ∈ (0, ∝), and ⇒ y strictly decreases in (0, e–1) ; strictly increases in (e–1, ∝).
Now, we have
The curve cuts the X-axis at (1, 0). The plot of the curve is shown above.
(d) We have y = lnx/x whose domain is x ∈ (0, ∝), and
⇒ y strictly increases in (0, e); strictly decreases in (e, ∝).
The curve cuts the X-axis at (1, 0). The plot of the curve is shown above.
(e) We have whose domain is x ∈ R ~ {1.7}, and
Now, we have
The curve cuts the Y-axis at (0, 1/7). The curve cuts the X-axis at (–1, 0). The plot of the curve is shown below.
(f) We have
The curve is symmetrical about the X-axis as well as the Y-axis. In the first quadrant the equation of the curve reduces to y = 2–x -1/2
whose plot is shown above.
The complete curve is drawn by taking the mirror image of the above shown curve in the X-axis and the Y-axis as shown alongside
Ex.32 Sketch a possible graph of a function f that satisfies the following conditions :
(i) f'(x) > 0 on (-∞, 1), f'(x) < 0n (1, ∞)
(ii) f''(x) > 0 on (-∞, -2) and (2, ∞), f''(x) < 0 on (-2, 2)
(iii) f(x) = - 2,
f(x) = 0
Sol. Condition (i) tells us that f is increasing on (- ∞, 1) and decreasing on (1, ∞). Condition (ii) says that f is concave upward on (-∞, -2) and (2, ∞), and concave downward on (-2, 2). From condition (iii) we know that the graph of f has two horizontal asymptotes: y = -2 and y = 0.
We first draw the horizontal asymptote y = -2 as a dashed line (see Figure). We then draw the graph of f approaching this asymptote at the far left, increasing to its maximum point at x = 1 and decreasing toward the x-axis at the far right. We also make sure that the graph has inflection points when x = -2 and 2. Notice that we made the curve bend upward for x < -2 and x > 2. and bend downward when x is between -2 and 2.
Maxima and Minima
Classification of Maxima & Minima
A function f(x) is said to have a local maximum at x = a if f(a) is greater than every other value assumed by f(x) in the immediate neighbourhood of x = a . Symbolically
⇒ x = a gives local maxima for a sufficiently small positive h .
Similarly, a function f(x) is said to have a local minimum value at x = b if f(b) is least than every other value assumed by f(x) in the immediate neighbourhood at x = b . Symbolically if
⇒ x = b gives local minima for a sufficiently small positive h .
Note that :
(i) The local maximum & minimum values of a function are also known as relative maxima or relative minima as these are the greatest & least values of the function relative to some neighbourhood of the point in question .
(ii) The term 'extremum' or 'turning point' is used both for local maximum or minimum values.
(iii) A local maximum (minimum) value of a function may not be the greatest (least) value in a finite interval.
(iv) A function can have several local maximum & minimum values & a local minimum value may even be greater than a local maximum value.
Fermat's Theorem
If f(x) has a local maximum or minimum at x = c and if f ' (c) exists, then f ' (c) = 0 .
(i) The set of values of x for which f ' (x) = 0 are often called as stationary points. The rate of change of function is zero at a stationary point.
(ii) In case f ' (c) does not exist, f(c) may be a maximum or a minimum.
The First Derivative Test
Suppose that c is a critical number of a continuous function f.
(a) If f' changes from positive to negative at c, then f has a local maximum at c.
(b) If f' changes from negative to positive at c, then f has a local minimum at c.
(c) If f' does not change sign at c (for example, if f' is positive on both sides of c or negative on both sides), then f has no local maximum or minimum at c.
In part (a), since the sign of f'(x) change from positive to negative at c, f is increasing to the left of c and decreasing to the right of c. It follows that f has local maximum at c.
It is easy to remember the First Derivative Test by visualizing the following diagrams.
Sufficient conditions for an extremum
If x0 is a critical point of the function f(x) and the inequalities f'(x0 - h) > 0, f'(x0 + h) < 0 are satisfied for an arbitrary, sufficiently small h > 0, then the function f(x) possesses a maximum at the point x0; now if f'(x0 + h) < 0, f'(x0 + h) > 0, then the function f(x) possesses a minimum at the point x0. If the signs of f'(x0 + h) and f'(x0 + h) are the same, then the function f(x) does not possess an extremum at the point x0.
Ex.1 Test the function y = (x - 2)2/3 (2x + 1) for extremum.
Sol. We find y' =
The critical points are x = 1 (the derivative is zero) and x = 2 (the derivative does not exist). The inequalities y'(1 - h) > 0, y'(1 + h) < 0, y'(2 - h) < 0, y' (2 + h) > 0 hold at a sufficiently small h > 0. Consequently, at the point x = 1 the function possesses a maximum ymax = 3 and at the point x = 2 it possesses a minimum ymin = 0.
Ex.2 Let f(x) = . Then find the value of `a' for which f(x) has local minimum at x=2.
Sol. We have f(x) =
f(x) has local minima at x = 2. Since, f(x) = 2x - 3 for x
2 (is strictly increasing)
a2 – 9a – 10 ≥ 0 ⇒ (a + 1) (a – 10) ≥ 0 ⇒ a ≤ –1 or a ≥ 10
Ex.3 Find the local maximum and minimum values of the function
Sol. To find the critical number of g, we differentiate : g'(x) = 1 + 2 cos x
So g'(x) = 0 when cos x =
The solutions of this equation are 2π/3 and 4π/3.
Because g is differentiable everywhere, the only critical numbers are 2π/3 and 4π/3 and so we analyze g in the following table.
Because g'(x) changes from positive to negative at 2π/3, the First Derivative Test tells us that there is a local maximum at 2π/3 and the local maximum value is
Likewise, g'(x) changes from negative to positive at 4π/3 and so
Ex.4 Find the values of a for which all roots of the equation 3x4 + 4x3 - 12x2 + a = 0 are real and distinct.
Sol. Consider the function f(x) = 3x4 + 4x3 - 12x2 + a.
Then f'(x) = 12(x3 + x2 - 2x) = 12x (x - 1) (x + 2).
From the sign scheme for f'(x), we can see that the shape of the curve will be as shown alongside.
For four real and distinct roots, the two minima must lie below the X-axis and the maxima must lie above the x-axis.
Thus, we have f(–2) < 0 i.e. 48 – 32 – 48 + a < 0 ...(i) i.e. a < 32
and f(1) < 0 i.e. 3 + 4 – 12 + a < 0 ...
(ii) i.e. a < 5
and f(0) > 0 i.e. a > 0 ...(iii)
Taking intersection of inequalities (1), (2) and (3) we have a ∈ (0, 5).
Ex.5 If f(x) = x3 + 3(a - 7) x2 + 3(a2 - 9) x - 1. If f(x) attains maxima at some positive value of x, then find the possible values of a.
Sol. We have f(x) = x3 + 3 (a - 7)x2 + 3(a2 - 9) x - 1 and f '(x) = 3x2 + 6(a - 7) x + 3 (a2 - 9)
which shows that there are two critical points (real or imaginary). According to the given condition, there is one real critical point (maxima), then the other critical point must also be real (minima).
Also, we have f(-∞) = -∞ and f(∞) = ∞
From the above facts, the graph of the curve y = f(x) can be drawn as shown alongside. Thus, if maxima occurs at some +ve value of x, then the minima must also occur at some +ve value of x(see fig.).
Thus, the roots of equation f '(x) = 0 are +ve and distinct, which is possible if discriminant > 0
i.e. (a – 7)2 > a2 – 9 i.e. –14 a + 58 > 0
i.e. a < 29/7 ...(1)
and product of the roots > 0
i.e. a2 – 9 > 0
i.e. a < –3 or a > 3 ...(2)
and sum of the roots > 0
i.e. a – 7 <0 i.e. a < 7 ...(3)
Drawing the number line for inequalities (1), (2), (3) and taking intersection, gives
Ex.6 For what real values of a and b are all the extrema of the function; f(x) = a2x3 - 0.5 a x2 - 2x - b, is positive and the minimum is at the point x0 = 1/3.
Sol. For extrema, f'(x) = 0 ⇒
a2 – a – 6 = 0 ⇒ a = –2, 3
So their arises two cases as :
Case I : at a = 3, if function attains minimum and is positive,
Case II : at a = -2, if function attains minimum and is positive,
Ex.7 For what values of `a' the point of local minima of f(x) = x3 - 3ax2 + 3(a2 - 1)x + 1 is less than 4 and point of local maxima is greater than -2.
Sol. f'(x) = 3(x2 - 2ax + a2 - 1)
Clearly roots of the equation f'(x) = 0 must be distinct and lie in the interval (-2, 4)
D > 0 ⇒ a ∈ R ...(1)
f'(–2) > 2 ⇒ a2 + 4a + 3 > 0 ⇒ a < –3 or a > –1 ...(2)
f'(4) > 0 ⇒ a2 – 8a + 15 > 0 ⇒ a > 5 or a < 3 ...(3)
From (1), (2) and (3) - 1 < a < 3
Alternate : f'(x) = 3(x - (a - 1)) (x - (a + 1))
clearly - 2 < a + 1 < 4 and -2 < a - 1 < 4 ⇒ -1 < a < 3
Extremum at End-points
A point (c, f(c)) is called an endpoint of the graph of the function f if there exists an interval (a, b) containing c such that the domain of f contains every number of the interval (a, c) and no number of the interval (c, b), or vice versa.
If (c, f(c)) is an endpoint of the graph of f such that f(c) is the maximum or minimum value of in some interval containing c, then f(c) is called an endpoint extremum of f. Note the difference between this definition and that of a relative extremum, in which it is assumed that some open interval containing c is contained in the domain of the function.
Consider f(x) = . Clearly, f(-2) = 0 and f(2) = 0 are endpoint extrema of f. Also, f(0) = 2 is a (relative) maximum value of f.
Second-Derivative Test For Extremum
Let c be a critical point of f in an open interval (a, b); that is, assume a < c < b and f'(c) = 0. Assume also that the second derivative f'' exists in (a, b). Then we have the following :
(a) If f'' is negative in (a, b), f has a relative maximum at c.
(b) If f'' is positive in (a, b), f has a relative minimum at c.
The two cases are illustrated in Figure
Proof. Consider case (a), f'' < 0 in (a, b). The function f' is strictly decreasing in (a, b). But f'(c) = 0, so f' changes its sign from positive to negative at c, as shown in Figure (a). Hence, f has a relative maximum at c. The proof in case (b) is entirely analogous.
If f'' is continuous at c, and if f''(c) 0, there will be a neighbourhood of c in which f'' has the same sign as f''(c). Therefore, if f'(c) = 0, the function f has a relative maximum at c if f''(c) is negative, and a relative minimum if f''(c) is positive. This test suffices for many examples that occur in practice.
Ex.8 Find all possible values of ' a ' for which the cubic f (x) = x3 + a x + 2 is non monotonic and has exactly one real root .
Sol. Note that
(i) for 3 real and distinct roots we have or f (x1) . f (x2) < 0 ⇒ f (x) is non monotonic in this case
(ii) for exactly one real root and monotonic the graph will be as shown. Here f ' (x)
0
(iii) for exactly one real root and non monotonic the graph will be as shown. Here f (x1) . f (x2) > 0
Now f (x) = x3 + a x + 2 ⇒ f ' (x) = 3 x2 + a
if a
0 , f (x) is always increasing .
Now let a < 0 f ' (x) = 0 ⇒ x =
f '' (x) = 6 x ; f '' > 0 ⇒ minima and f '' < 0 ⇒ maxima
for exactly one real root and non monotonic (case iii)
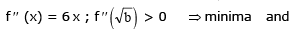
for exactly one real root and non monotonic (case iii)
Note that
(i) for a = - 3 , f (x) = x3 - 3 x + 2 = (x + 2) (x - 1)2 i.e. f (x) has two coincident roots .
(ii) for a < - 3 , f (x) has 3 real and distinct roots
(iii) for a
0 , f (x) is exactly real root and is always monotonic increasing find (x2 - x1)2 from (1) and get V as a function of y
Ex.9 Let 'p' & 'q' be real numbers . Prove that the cubic y = x3 + p x + q has three distinct real roots, if 4 p3 + 27 q2 < 0 .
Sol.
Let f (x) = x3 + p x + q ⇒ f'(x) = 3 x2 + p
If p > 0 ⇒ no root ( f (x) is monotonic)
3 distinct real roots f (x) must have exactly one maxima & minima .
Ex.10 Suppose f(x) is real valued polynomial function of degree 6 satisfying the following conditions ;
(a) f has minimum value at x = 0 and 2
(b) f has maximum value at x = 1
(c) for all x, = 2 .
Sol.
⇒ f(x) have co-efficient of x3, x2, x or constant term zero in order that the limit may exist.
Hence f(x) = ax6 + bx5 + cx4 ⇒ f'(x) = x3 (6 ax2 + 5 bx + 8)
f'(1) = 0 and f'(2) = 0 gives 6a + 5b + 8 = 0 and 24 a + 10 b + 8 = 0
Global Maximum and Minimum
A function f has an absolute maximum (or global maximum) at c if f (c) ≥ f(x) for all x in D, where D is the domain of f. The number f(c) is called the maximum value of f on D. Similarly, f has an absolute minimum at c if f(c) ≤ f(x) for all x in D and the number f(c) is called the mini mum value of f on D. The maximum and minimum values of f are called the extreme values of f
Figure shows the graph of a function f with absolute maximum at d and absolute minimum at a. Note that (d, f(d)) is the highest point on the graph and (a, f(a)) is the lowest point.
The Extreme Value Theorem
If f is continuous on a closed interval [a, b], then f attains an absolute maximum value f(c) and an absolute minimum value of f(d) at some numbers c and d in [a, b].
The Extreme Value Theorem is illustrated in Figure 1. Note that an extreme value can be attained at more than one point. Although the Extreme Value Theorem is intuitively very plausible, it is difficult to prove and so we omit the proof.
Conditions of Extreme Value Theorem
Figure 2, 3 show that a function need not possess extreme values if either hypothesis (continuity or closed interval) is omitted from the Extreme Value Theorem. The function f whose graph is shown in Figure 2 is defined on the closed interval [0, 2] but has no maximum value. (Notice that the range of f is [0, 3). The function takes on values arbitrarily close to 3, but never actually attains the value 3.) This does not contradict the extreme value theorem.
The function f shown in Figure 3 is continuous on the open interval (0, 2) but has neither a maximum nor a minimum value. The range of g is (1, ∝). The function takes on arbitrarily large values.] This does not contradict the Extreme Value Theorem because the interval (0, 2) is not closed.
In each case, explain why the given function does not contradict the extreme value theorem.
a. The function f has no maximum. It takes on all values arbitrarily close to 2, but it never reaches the value 2. The extreme value theorem is not violated because f is not continuous on [0, 2].
b. Although the functional values of g(x) become arbitrarily small as x approaches 0, it never reaches the value 0, so g has no minimum. The function g is continuous on the interval (0, 2], but the extreme value theorem is not violated because the interval is not closed.
Procedure for Finding the Extrema of a Continuous Function
Suppose a continuous function f is differentiable at all except a finite number of values of x in its domain, the closed interval
1. Find all x in a < x < b that satisfy the equation f'(x) = 0 or at which f'(x) does not exist; let x = r, x = s, x = t, .... be such x. The numbers r, s, t, . . . are often called critical points of f.
2. Evaluate f at each critical point; that is, find f(r), f(s), f(t),........
3. Evaluate f(a) and f(b).
4. The largest of the numbers computed in Step 2 and Step 3 is the maximum of f(x) for a £ x £ b, and the smallest number is the minimum.
Ex.11 Let f(x) = 2x3 - 9x2 + 12x + 6. discuss the global maxima and global minima of f(x) in (1, 3).
Sol.
f(x) = 2x3 – 9x2 + 12x + 6 ⇒ f'(x) = 6x2 – 18x + 12 ⇒ f'(x) = 6 (x – 1) (x – 2)
let f'(x) = 0 ⇒ x = 1, 2. ∴ f(1) = 11 and f(2) = 10 ...(i)
let us consider the open interval (1, 3). Clearly x = 2 is the only point in (1, 3) and f(2)=10 [from (i)
Thus, x = 2 is the point of global minima in (1, 3) and global maxima does not exist in (1, 3).
Ex.12 Let w(x) = 4x2 - 3x2 on - < x <
. Discuss the extrema of w.
Sol. w(x) has a maximum at x = 0 and a minimum at x = 1/2 , and these two values are in the given interval.
Ex.13 The greatest value of the function f(x) = in the interval [- 1, 1] is
Sol. f'(x) = 2.3x . l n 3 [ 3.32x - 4.3 x + 2 ]
Hence f (x) is greatest when x = 1 & f (1) = 24
Ex.14 Let f (x) = ax2 - 4ax + b (a > 0) be defined in Suppose the average of the maximum value and the minimum value of the function is 14, and the difference between the maximum value and minimum value is 18. Find the value of a2 + b2.
Sol.
f (x) = ax2 – 4ax + b (a > 0) ⇒ f ' (x) = 2ax – 4a = 0
at x = 2 also, f ' (x) = 2a(x – 2) ⇒ for x ∈ (1, 2) f is
Hence minimum occurs as x = 2
f (2) = 4a – 8a + b
f(2) = b – 4a
maximum will occur at f (5) and
M – m = 9a = 18 ⇒ a = 2 also M+m/2 = 14 ⇒ M + m = 28 = 2b + a ⇒ b = 13
Hence a = 2 and b = 13
a2 + b2 = 4 + 169 = 173
Ex.15 If f(x)= and f(x) = 0 has both non-negative roots, then prove that
Sol. Given that f(x) = (x - a) (x - b) -
Sum of the root of the equation f(x) = 0, will be positive ⇒ (a + b) > 0
The product of the roots of the equation will be greater than and equal to zero
Now f(x) will be minimum, when f'(x) = 0 ⇒ x =a+b/2
Ex.16 If x > 0, let f(x) = 5 x2 + A x -5 , where A is a positive constant. Find the smallest A such that for all x > 0 .
Sol.
f ' (x) = 10 x - 5 A x -6 and f '' (x) = 10 + 30 A x -7 > 0 i.e. f ' (x) = 0 gives a minima
Since A > 0 ⇒ we get only one minima and no maxima . Hence smallest value of f(x) will be at
Ex.17 Find the sum of the local maximum and local minimum values of the function f (x) =
Sol.
⇒ (t – 3t2)y = 3 – t , 3yt2 – (1 + y)t + 3 = 0
t > 0 ⇒ D ≥ 0 ; Sum of roots > 0 ; Product of roots >
hence (1 + y)2 – 36y ≥ 0;
⇒ y2 – 34y – 1 ≥ 0 ⇒ (y – 17)2 ≥ 288
⇒ (y – 17 – 12√2 )(y – 17 + 12√2 ) ≥ 0
⇒ [y – (17 + 12√2 )] [y – (17 – 12√2 )] ≥ 0
Hence ymax = 17 – 12√2 , ymin = 17 + 12√2 ⇒ ymax + ymin = 34 which is rational
Ex.18 For a certain curve = 6x - 4 and y has a local maximum value 5 when x = 1 . Find the equation and the global maximum and minimum values of y, given that
Sol.
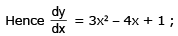
Integrating again, y = x3 - 2x2 + x + B ; y]x = 1 ⇒ B = 5.
Thus y = x3 - 2x2 + x + 5.
given x = 1/3 and z = 1 f(1/3) =139/27; f(1) = 5
also f(0) = 5 ; f(2) = 7 . Hence GMV = 7 ; gmv = 5
Ex.19 Find the least and the greatest value of f(x, y) = x2 + y2 - xy where x and y are connected by the relation x2 + 4y2 = 4.
Sol.
Here x2 + 4y2 = 4
⇒
⇒ Let x = 2 cos θ, y = sinθ
Hence, f(x, y) = x2 + y2 – xy = 4 cos2θ + sin2θ –2 sinθ cosθ = 2 (1 + cos 2θ) + 1/2 (1 - cos 2θ) - sin2θ
“Since we know a sinθ + b cosθ lies between
Thus, greatest value of f(x, y) =
and least value of f(x, y)
G. Geometrical Problems
Working Rule
1. When possible , draw a figure to illustrate the problem & label those parts that are important in the problem . Constants & variables should be clearly distinguished.
2. Write an equation for the quantity that is to be maximized or minimized . If this quantity is denoted by `y' , it must be expressed in terms of a single independent variable x . This may require some algebraic manipulations.
3. If y = f (x) is a quantity to be maximum or minimum, find those values of x for which f '(x) = 0 or f'(x) does not exist.
4. Test each value of x to determine whether it provides a maximum or minimum or neither. The usual tests are:
(a) If d²y/dx² is positive when dy/dx = 0 ⇒ y is minimum.
If d²y/dx² is negative when dy/dx = 0 ⇒ y is maximum.
If d²y/dx² = 0 when dy/dx = 0, the test fails.
(b) ⇒ a maximum occurs at x = x0.
But if dy/dx changes sign from negative to zero to positive as x advances through xo there is a minimum. If dy/dx does not change sign, neither a maximum nor a minimum.
5. If the function y = f (x) is defined for only a limited range of values then examine x = a & x = b for possible extreme values.
Useful Formulae Of Mensuration
- Volume of a cuboid = lbh .
- Surface area of a cuboid = 2 (lb + bh + hl) .
- Volume of a prism = area of the base x height .
- Lateral surface of a prism = perimeter of the base x height .
- Total surface of a prism = lateral surface + 2 area of the base (Note that lateral surfaces of a prism are all rectangles) .
- Volume of a pyramid = 1/3 area of the base x height .
- Curved surface of a pyramid = 1/2 (perimeter of the base) x slant height .
- (Note that slant surfaces of a pyramid are triangles) .
- Volume of a cone = 1/3πr2h
- Curved surface of a cylinder = 2 πrh .
- Total surface of a cylinder = 2πrh + 2πr2
- Volume of a sphere = 4/3πr3
- Surface area of a sphere = 4πr2
- Area of a circular sector = 1/2r2 θ, when θ is in radians.
Ex.20 A trapezium ABCD is inscribed into a semicircle of radius l so that the base AD of the trapezium is a diameter and the vertices B & C lie on the circumference . Find the base angle q of the trapezium ABCD which has the greatest perimeter .
Sol. Hint : P = AB + BC + CD + DA = (AB + CD) + BC + DA
CD = AB = 2 l cos θ ; AD = 2 l and
x = AB cos θ ⇒ BC = 2 l - 2 x = 2 l - 2 AB cosθ = 2 l - 4 l cos2θ
Hence P = 4 l + 4 l cosθ - 4 l cos2 θ
Ex.21 A bus contractor agrees to run special buses for the employees of ABC Co. Ltd . He agrees to run the buses if atleast 200 persons travel by his buses . The fare per person is to be Rs. 10/- per day if 200 travel and will be decreased for everybody by 2 praise per person over 200 that travels . How many passengers will give the contractor maximum daily revenue ?
Sol. Let number of passengers be x, which will yield maximum profit
⇒ f'(x) = 0 ⇒ x = 350 ; f(x)]max = 2450
Ex.22 Find the radius of the smallest circular disk large enough to cover every isosceles triangle of a given perimeter L.
Sol.
Ex.23 Through a point A on the circumference of a circle of radius r, two straight lines are drawn enclosing an angle f . If the straight lines meet the circle again at B & C, find the maximum area of triangle ABC .
Sol.
A = 2r2 sin ø sin ø sin (θ +ø) = r2 sinø [ cosø- cos (2θ +ø) ]
Ans. : r2 sin ø (1 + cosø) sq. units
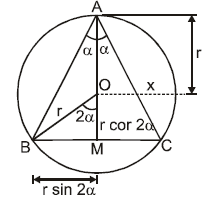
Ex.24 An isosceles triangle is inscribed in a circle of radius r . If the angle 2 α at the apex is restricted to lie between find the largest and the smallest value of the perimeter of the triangle . Give sufficient details of your reasoning .
Sol.
P = f (α) = 4 r (1 + sin α) cos α
f'(α) = 4 r [ cos2 α - (1 + sin α) cos α] = 4 r (1 - 2 sin α) (1 + sin α)
Ex.25 The plan view of a swimming pool consists of a semicircle of radius r attached to a rectangle of length '2r' and width 's' . If the surface area A of the pool is fixed, for what value of 'r' and 's' the perimeter 'P' of the pool is minimum .
Sol.
Ex.26 Find the altitude of a cone of the least volume that can be drawn around a hemisphere of radius R (the centre of the base of the cone falls on the centre of the sphere).
Sol.
Let AO = H, BO = r = radius of the base of the cone
R = radius of the hemisphere, ∠OAC = θ (θ ∈(0, π/2))
Clearly V(θ) has only one critical point namely θ = sin-1 1/√3 .Using sign scheme for V'(θ)
we get, θ = sin-1 1/√3 to be the point of maxima. Hence corresponding altitude H R/sinθ = R√3 .
Ex. 27 What normal to the curve y = x2 forms the shortest chord.
Sol. Let (t, t2) be any point on the parabola y = x2
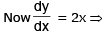
So, the slope of the normal to y = x2 at (t, t2) is (-1/2t)
The equation of the normal to y = x2 at (t, t2) is y – t2 =(-1/2t) (x-t)....(1)
Suppose equation (i) meets the curve again at B(t1, t12), then,
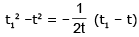
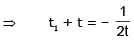
Let L be the length of the chord AB (as normal)
L = AB2 = (t – t1)2 + (t2 – t12)2 = (t – t1)2 [1 + (t + t1)2]
⇒ equation of normal AB is √2 x + 2y – 2 = 0 and √2 x – 2y + 2 = 0
Ex.28 The circle x2 + y2 = 1 cuts the x-axis at P and Q. Another circle with centre at Q and variable radius intersects the first circle at R above the x-axis and the line segment PQ at S. Find the maximum area of the triangle QSR.
Sol. The centre of the circle x2 + y2 = 1 ....(i) is (0, 0) and radius OP=1=OQ so, co-ordinates of Q are (1, 0)
Let the radius of the variable circle be r. Hence, its equation is (x - 1)2 = (y)2 = r2 ...(ii)
Hence, area is maximum at
Maximum and Minimum for Discrete Valued Functions
Ex.29 Find the largest term in the sequence an =
Sol.
⇒ f(x) strictly increases in (0, √10 ) strictly decreases in ( 10 , ∝)
⇒ f(x) has greatest value at x = √10
Hence, the given sequence has greatest value at n = 3 or n = 4.
Now, we have a3 = 3/19 and a4 = 4/26. Hence, a3 = 3/19. is the largest term of the given sequence.
I. Concavity and Point of Inflection
The graph of the function y = f(x) is said to be concave down on the interval (a, b) if it lies below the tangent drawn at any point of that interval (Fig. 1).
The graph of the function y = f(x) is said to be concave up on the interval (a, b) if it lies above the tangent drawn at any point of that interval (Fig. 2).
The sufficient condition for the concavity of the graph of a function.
If f''(x) < 0 on the open interval (a, b) then the graph of the function is concave down on that interval; now if f''(x) > 0, then on the open interval (a, b) the graph of the function is concave up.
The point (x0; f(x0)) of the graph of the function separating its concave down part from the concave up part is called a point of inflection (Fig. 3).
If x0 is the abscissa of the inflection point of the graph of the function y = f(x), then the second derivative is equal to zero or does not exist. The points at which f''(x) = 0 or f''(x) does not exist are called critical points of the 2nd kind.
If x0 is a critical point of the 2nd kind and the inequalities f''(x0 - h) < 0, f''(x0 + h) > 0 (or inequalities f''(x0 - h) > 0, f''(x0 + h) < 0) hold for an arbitrary sufficiently small h > 0, then the point of the curve y = f(x) with the abscissa x0 is a point of inflection.
If f''(x0 - h) and f''(x0 + h) are of the same sign, then the point of the curve y = f(x) with the abscissa x0 is not a point of inflection.
Ex.30 Find the intervals of concavity of the graph of the function y = x5 + 5x - 6.
Sol. We have y' = 5x4 + 5, y'' = 20x3. If x < 0, then y'' < 0 and the curve is concave down ; now if x > 0, then y'' > 0 and the curve is concave up. Thus we see that the curve is concave down on the interval (-∞, 0) and concave up on the interval (0, + ∞).
Ex.31 Find the inflection points of the curve y = (x - 5)5/3 + 2.
Sol. We find
The second derivative does not vanish for any value of x and does not exist at x = 5. The value x = 5 is the abscissa of the inflection point since y'' (5 - h) < 0, y''(5 + h) > 0. Thus, (5, 2) is the inflection point. Inflection points can also occur if
fails to exist .
Cusp :
A point on a graph where the curve makes an abrupt change in direction is called a cusp. Our next example features a graph with such a point.
Find the first and second derivatives and write them in factored form.
Let f(x) = 2x5/3 + 5x2/3.
Note that the graph is concave down on both sides of x = 0 and that the slope f'(x) decreases without bound to the left of x = 0 and increases without bound to the right. This means the graph changes direction abruptly at x = 0, and we have a cusp at the origin.
Ex.32 Prove that for any two numbers x1 & x2
Sol.
Assume f(x) = ex and let x1 & x2 be two points on the curve y = ex.
Let R be another point which divides P and Q in ratio 1 : 2.
y coordinate of point R is
and y coordinate of point S is
.Since f(x) = ex is always concave up, hence point R will always be above point S
(above inequality could also be easily proved using AM and GM.)
Ex.33 If 0 < x1 < x2 < x3 < then prove that sin
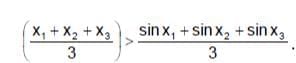 . Hence or otherwise prove that if A, B, C are angles of triangle then maximum value of sinA + sin B + sin C is
. Hence or otherwise prove that if A, B, C are angles of triangle then maximum value of sinA + sin B + sin C is
Sol.
Let point A, B, C form a triangle y coordinate of centroid G is
and y coordinate of point F is
If A + B + C = π , then
⇒ maximum value of (sin A + s in B + s in C)
|
177 videos|620 docs|160 tests
|
FAQs on Notes: Applications of Derivatives - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of a tangent and a normal line in calculus? |  |
| 2. How do you find the length of a tangent from a point to a curve? |  |
| 3. What is the significance of increasing and decreasing functions in calculus? |  |
| 4. How can one use derivatives to test for increasing and decreasing functions? |  |
| 5. What is the shortest distance from a point to a line, and how is it calculated? |  |