Notes: Nature of Mathematics | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download
Mathematics is a universal language that helps us understand the world through numbers, symbols, and logical reasoning. It is not just about calculations but also about patterns, relationships, and problem-solving. The nature of mathematics lies in its precision, structure, and ability to develop analytical thinking.
For educators preparing for the CTET exam, understanding mathematics is essential for fostering curiosity, logical reasoning, and problem-solving skills in students. Effective mathematics teaching involves a balance of theoretical understanding, practical applications, and engaging teaching strategies. This document explores the fundamental characteristics of mathematics, its role in education, and various teaching methodologies that enhance learning outcomes.

The term 'Mathematics' refers to the science where calculations are paramount. It encompasses the study of numbers, words, signs, and concepts, allowing us to understand magnitude, direction, and space.
"Mathematics should be visualized as the vehicle to train a child to think, reason, analyze, and articulate logically. Apart from being a specific subject, it should be treated as a concomitant to any subject involving analysis and meaning."
Definitions
In Hindi, Mathematics is known as ‘GANITA’, which means 'The Science of calculations'.According to the Oxford Dictionary, "Mathematics is the Science of measurement, quantity, and magnitude."
Several notable definitions of Mathematics include:
"Mathematics is the study of abstract systems built of abstract elements. These elements are not described in concrete form." – Marshal H. Stone
"Mathematics is a way to settle the habit of reasoning in the mind of children." – John Locke
Conclusions
Based on the above definitions, we can conclude that:
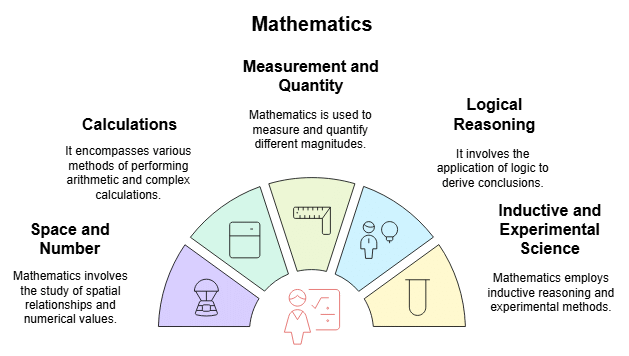
- Mathematics is the Science of space and number.
- Mathematics is the Science of calculations.
- Mathematics is the Science of measurement, quantity, and magnitude.
- Mathematics is a systematized, organized, and exact branch of Science.
- It deals with quantitative facts and relationships.
- It is the abstract form of Science.
- It is the Science of logical reasoning.
- It settles the habit of reasoning in the mind.
- It is an inductive and experimental Science.
- Mathematics is the Science which draws necessary conclusions.
Mathematics holds a strong and unbreakable position compared to other school subjects. For this reason, Mathematics is more stable and important. As the structure of a subject weakens, its truthfulness, reliability, and predictive power decrease correspondingly. The nature of each subject is determined based on its specific structure and placed in the school curriculum accordingly.
Features of Mathematics
The nature of Mathematics can be understood through the following features:
- Mathematics is the Science of space, numbers, magnitude, and measurement.
- Mathematics has its own language, including mathematical terms, concepts, formulae, theories, principles, and signs.
- Mathematics involves converting abstract concepts into concrete forms.
- Mathematics eliminates doubts in learners' minds about theories, principles, and concepts.
- Mathematics helps develop self-confidence and self-reliance in children.
- Mathematics fosters a sense of appreciation in children.
- Mathematics promotes the development of a scientific attitude in children.
- The study of Mathematics trains children in scientific methods.
- Mathematical knowledge is based on sense organs.
- Mathematics provides accurate and reliable knowledge.
- Mathematical knowledge is exact, systematic, logical, and clear, making it unforgettable once acquired.
- Mathematical rules, laws, and formulae are universal and verifiable at any time and place, aiding in the development of inductive, deductive, and generalization abilities.
- Mathematical language is well-defined, useful, and clear.
- Mathematics draws numerical inferences based on given information and data.
- Mathematical knowledge is applied in the study of Science and its various branches, such as Physics, Chemistry, and Biology.
- Mathematics not only supports different branches of Science but also helps in their progress and organization.
As Roger Bacon stated, "Mathematics is the gateway and key of all sciences."
Teaching in Mathematics
In Mathematics, teaching and teaching techniques are aids used to make lessons interesting, explain content, and help students remember it during the teaching-learning process. While techniques are not directly linked to teaching objectives, they are connected to teaching methods, which are directly linked to teaching objectives.Teaching strategies, on the other hand, are purposefully conceived and determined plans of action. Instructional strategies refer to patterns of teaching acts that aim to achieve certain outcomes and avoid others.
Various Strategies and Techniques of Teaching Mathematics
- Self Study
- Drill Work
- Supervised Study
- Homework/Home Assignment
- Review
- Oral Work
- Brainstorming
- Written Work
- Assignment
- Group Work
Drill in Mathematics
Drill and exercises play a crucial role in Mathematics teaching and learning. Drill work is based on psychological principles such as learning by doing and the law of exercise. It provides a convenient and efficient medium for rapid memorization of details and the automation of processes.
Drill is essential for attaining desired controls, just as emphasizing concepts and meanings is crucial for understanding. Both are necessary; neither alone is sufficient. Drill offers opportunities for self-learning and improvement. Speed and accuracy in Mathematics cannot be achieved without drill work.
Ensure that understanding precedes drill. Otherwise, practice becomes an exercise in academic futility.
How to Make Drill Effective
To make drill exercises effective, consider the following points:
- Conduct drill exercises so that pupils can work at different rates and levels according to their abilities.
- Keep drill exercises brief and spread them over a period of time.
- Include several distinct activities that involve different learning strategies.
- Incorporate a variety of problems to maintain interest.
- Ensure the drill work is progressively more challenging.
Importance/Advantages of Drill Work
- Helps retain learnt material for a longer time.
- Is an effective learning technique for beginners.
- Allows adjustment of the learning speed according to need.
- Improves accuracy of learnt material.
- Tests the memory of the child.
Disadvantages of Drill Work
- Not suitable for all topics.
- Can cause disturbances in other classes.
- Not effective without a good and clear voice.
- Can become an exercise in academic futility if not done correctly.
- Requires careful questioning by the teacher
Homework in Mathematics
In modern secondary school curriculums, the vast amount of content requires teachers to supplement classroom learning with homework. Regular homework is essential to cover the heavy curriculum load and to ensure students practice and apply what they have learned in class.Mathematics homework may include problems based on classroom lessons, learning principles, definitions, and drawing graphs, charts, and tables. The goal is to create a study environment at home. Homework should be appropriate to the capacities of the students and should be assessed as part of internal assessment with proper weightage given.
Objectives of Homework
- Utilizes the child's leisure time productively.
- Cultivates habits of regularity and hard work.
- Provides opportunities for independent work.
- Allows for the application and practice of acquired knowledge.
Importance/Advantages of Homework
- Essential due to insufficient school hours for necessary work.
- Fosters closer relationships between parents and the school.
- Promotes the habit of self-study in children.
- Develops a sense of responsibility in children.
- Encourages progress through the constant requirement of homework.
Disadvantages of Homework
- Can take up too much of the children's time after school.
- Home environments may not provide suitable conditions for work.
- Some students rely on parents or others to complete their homework.
- Can cause emotional tensions in some children.
- Sometimes used as a form of punishment, which is counterproductive.
Oral Work in Mathematics
Oral work in Mathematics is not only interesting but also effective, especially in the initial stages. It saves time and effort by omitting certain steps and aids in mental calculations. Oral work provides a quick and easy start to the learning process. Lessons can be introduced through short, simple, and appropriate oral questions, making them easily comprehensible and clarifying the learning process.
Oral questions can be graded by difficulty and help develop careful listening, visualization, quick thinking, and decision-making skills. They also help identify a child's weaknesses, allowing for immediate correction of mistakes. New processes and methods should initially be introduced orally to spark interest in the new material. Once oral work is completed, it should be followed by written work.
Importance/Advantages of Oral Work
- Tests the child's memory.
- Develops confidence in the learning process.
- Enhances thinking, understanding, and imagination.
- Allows for quick revision of the subject matter.
- Checks the student's prior knowledge before introducing new topics.
- Increases attentiveness in class, as any student can be asked to answer oral questions at any moment.
Disadvantages of Oral Work
- Does not provide a record of the learned material for future reference.
- Is a quick method and may not be suitable for all students.
- Not all problems can be solved verbally.
- Cannot properly assess the students' writing abilities.
- May not help retain learning material for a long time.
Written Work in Mathematics
To achieve precision and accuracy, written work is essential in Mathematics. Oral discussions alone are not enough. Based on the psychology of visual and auditory learners, it is clear that not all children benefit solely from oral work. Therefore, oral work must be supplemented by written work. Combining both techniques makes the instructional process complete. Mental work should be paired with written work to enhance teaching and learning.Written work allows teachers to assess the amount of work done by students and test the knowledge imparted orally. It ensures students follow proper rules, processes, and principles.
Importance/Advantages of Written Work
- Learning through this technique is retained for a longer time.
- Tests the child's memory effectively.
- Properly assesses the student's expression and writing abilities.
- Provides opportunities for improving handwriting if needed.
- Builds confidence and reinforces the learning process.
- Allows for accurate identification and correction of mistakes.
Disadvantages of Written Work
- Is a time-consuming technique.
- Can be laborious.
- Not suitable for beginners, as learning tables and counting can be more effectively done through proper drill work.
- Cannot be carried out independently without prior oral instructions.
- Not suitable for physically handicapped children.
Group Work in Mathematics
In Mathematics, group work provides ample opportunities for collaborative learning. Activities, projects, assignments, and practical work all facilitate group engagement, enhancing the learning experience.Characteristics of Group Work
- Groups should be homogeneous in terms of intelligence and achievement levels.
- Two heads are better than one, promoting the exchange of ideas and opinions.
- Encourages competitive cooperation among group members.
- Utilizes the experience and learning of each group member.
- Most effective for children aged eight to twelve years.
- Clear purpose and objectives are essential for successful group work.
Essential Constituents of Group Work
- The teacher
- The problem
- The contents
- The group
- Evaluation
Self Study in Mathematics
Self study involves independent learning, where individuals solve problems on their own without outside help. Regular homework or assignments, projects, debates, discussions, seminars, and competitions all contribute to effective self study.Importance of Self Study
- Develops a sense of responsibility and regularity.
- Encourages independent work and use of personal knowledge and experiences.
- Discourages cramming habits.
- Ensures proper utilization of leisure time.
- Fosters heuristic and problem-solving attitudes.
- Serves as an excellent supplement to class work.
Supervised Study in Mathematics
Supervised study is a crucial technique in Mathematics teaching, where the teacher guides and supports students, addressing individual problems and promoting self study habits. It ensures regular progress and helps rectify mistakes on the spot.Steps for Supervised Study
- Introduction and preparation for study.
- Instructions for the study.
- Teacher supervision.
- Development of a blackboard summary.
Importance/Characteristics of Supervised Study
- Provides an opportunity for every child to learn according to their ability and capacity.
- Develops the habit of self study.
- Based on the principles of activity and individual differences, promoting a disciplined atmosphere.
- The teacher acts as a guide, ensuring both teacher and students remain active.
Precautions for Supervised Study
- Encourage freedom and mutual exchange of ideas and views.
- Keep study periods reasonably short.
- Teachers should possess insight and resourcefulness.
- Emphasize the development of scientific attitudes and mathematical reasoning.
- Select topics based on the interests, attitudes, needs, and capacities of the students, focusing on developing problem-solving abilities.
Effective Mathematics Learning Techniques
Review in Mathematics
Review and drill work are often associated due to their repetitive nature and focus on reinforcing concepts. However, while drill aims at automatisation of detailed processes, review focuses on the thoughtful organization and retention of key concepts within a unit or chapter, ensuring the clear understanding of the relationships between various parts and the whole.
Review emphasizes thought and meaning, enhancing recall effectiveness. It provides a new perspective on the material studied, making it a crucial component in the study of mathematics.
Assignment in Mathematics
An assignment involves work given to students before or after a lesson, to be completed at school or home. It represents a commitment on the part of the learner, fostering responsibility. Assignments should be brief and include both repetitive and review problems.Types of Assignment Problems
- Repetitive Problems: Based on new work, these emphasize aspects of newly learned material, helping students understand and retain new concepts.
- Review Problems: These spiral back over previously learned skills and concepts, ensuring continuous reinforcement and retention of material.
Purposes of Assignments in Mathematics
- To solve mathematical problems.
- To prepare illustrations for a topic.
- To collect mathematical data.
- To solve problems based on a proposition.
- To understand a proposition or a group of propositions.
- To trace the background of a mathematical problem or concept.
- To formulate problems on a topic or concept.
Characteristics of Good Assignments
- Correlates with the previous knowledge of the child.
- Addresses and removes difficulties faced by the child.
- Clear and definite in its instructions.
- Stimulates and directs the child’s learning activities.
How to Make an Assignment Effective
- Provide proper hints and ensure the assignment is insightful, not just a dictation of questions.
- Motivate students and clear any doubts or misunderstandings.
- Encourage cooperative activity between the teacher and students.
- Facilitate interaction between pupils and teachers.
- Use reference books, textbooks, and other materials to stimulate and direct assignment activities.
Brainstorming in Mathematics
Brainstorming is a democratic, problem-centered technique that encourages creativity and originality among students. It relies on the assumption that children learn better in groups than individually.
The teacher assigns a problem, and students independently think about it before engaging in discussion and debate. Ideas and views are shared openly, with the teacher recording them for collective problem-solving.
Importance/Advantages of Brainstorming
- Promotes problem-oriented learning.
- Helps achieve higher-order cognitive and affective objectives.
- Encourages democratic learning environments.
- Provides a platform for diverse ideas and views.
|
82 videos|273 docs|69 tests
|
FAQs on Notes: Nature of Mathematics - Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET
| 1. What are the key features of mathematics? |  |
| 2. How can effective teaching techniques improve mathematics learning? |  |
| 3. What role does homework play in mathematics education? |  |
| 4. Why is group work important in learning mathematics? |  |
| 5. What are some effective self-study techniques for mastering mathematics? |  |

















