Numerical Methods | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: Consider the data of f(x) given in the table. 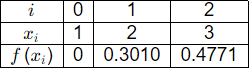 The value of f(1.5) estimated using second-order Newton's interpolation formula is (rounded off to 2 decimal places). (2024 SET-1)
The value of f(1.5) estimated using second-order Newton's interpolation formula is (rounded off to 2 decimal places). (2024 SET-1)
Ans: 0.16 to 0.18
Sol: It is based on 2nd order interpolation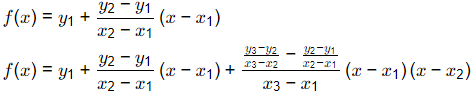
Here,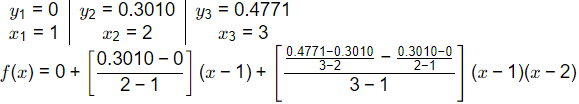
f(x) = 0.3010(x − 1) + ((-0.1249)/2) (x − 1)(x − 2)
f(x) = 0.3010(1.5 − 1) + ((-0.1249)/2) (1.5 − 1)(1.5 − 2)
f(1.5) = 0.1505 + 0.0156 = 0.1661
Q1: A function f(x), that is smooth and convex-shaped between interval (x1, xu) is shown in the figure. This function is observed at odd number of regularly spaced points. If the area under the function is computed numerically, then ____ (2023 SET-1)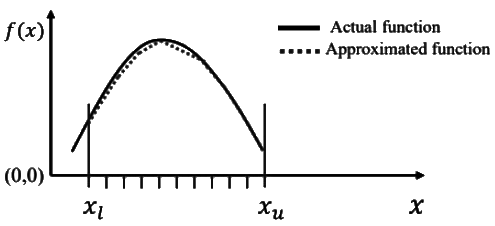 (a) the numerical value of the area obtained using the trapezoidal rule will be less than the actual.
(a) the numerical value of the area obtained using the trapezoidal rule will be less than the actual.
(b) the numerical value of the area obtained using the trapezoidal rule will be more than the actual.
(c) the numerical value of the area obtained using the trapezoidal rule will be exactly equal to the actual.
(d) with the given details, the numerical value of area cannot be obtained using trapezoidal rule.
Ans: (a)
Sol: Approximated function has under estimation so numerical value of the area obtained using trapezoidal rule will be less than the actual.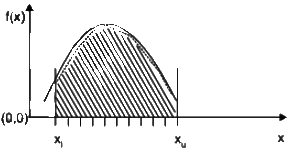
Q1: Consider the following recursive iteration scheme for different values of variable P with the initial guess x1 = 1 :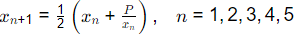
For P = 2, x5 is obtained to be 1.414, rounded-off to three decimal places. For P = 3, x5 is obtained to be 1.732, rounded-off to three decimal places.
If P = 10, the numerical value of x5 is _________ . (round off to three decimal places) (2022 SET-1)
Ans: 3.1 to 3.2
Sol: 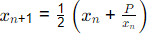
Converges when xn + 1 = xn = α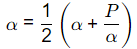
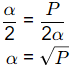
When P = 2, x5 = √2 = 1.4124
When P = 3, x5 = √3 = 1.732
When P = 10, x5 = √10 = 3.162
Q1: Numerically integrate, f(x) = 10x − 20x2 from lower limit a = 0 to upper limit b = 0.5. Use Trapezoidal rule with five equal subdivisions. The value (in units,round off to two decimal places) obtained is __________ (2021 SET-2)
Ans: 0.38 to 0.42
Sol: y = 10x - 20x2
a = 0, b = 0.5, n = 5
So, h = (b-a)/n = 0.1
And
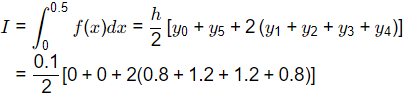
= 0.40
Q2: The value of 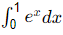 using the trapezoidal rule with four equal subintervals is (2021 SET-1)
using the trapezoidal rule with four equal subintervals is (2021 SET-1)
(a) 1.718
(b) 1.727
(c) 2.192
(d) 2.718
Ans: (b)
Sol: Let 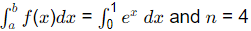
Then 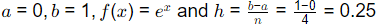
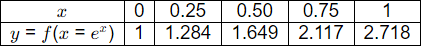
The formula of trapezoidal rule to the given data is given by
Q1: The integral 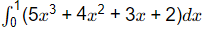 is estimated numerically using three alternative methods namely the rectangular, trapezoidal and Simpson's rules with a common step size. In this context, which one of the following statement is TRUE? (2020 SET-2)
is estimated numerically using three alternative methods namely the rectangular, trapezoidal and Simpson's rules with a common step size. In this context, which one of the following statement is TRUE? (2020 SET-2)
(a) Simpsons rule as well as rectangular rule of estimation will give NON-zero error.
(b) Simpson's rule, rectangular rule as well as trapezoidal rule of estimation will give NON-zero error.
(c) Only the rectangular rule of estimation will given zero error.
(d) Only Simpson's rule of estimation will give zero error.
Ans: (d)
Sol: Because integral is a polynomial of 3rd degree so Simpson's rule will give error free answer.
Q1: The value of the function f(x) is given at n distinct values of x and its value is to be interpolated at the point x*, using all the n points. The estimate is obtained first by the Lagrange polynomial, denoted by IL and then by the Newton polynomial, denoted by IN. Which one of the following statements is correct? [2019 : 1 Mark, Set-ll]
(a) IL is always greater than IN
(b) No definite relation exists between IL and IN
(c) IL and IN are always equal
(d) IL is always less than IN
Ans: (c)
Q1: The quadratic equation 2x2 - 3x + 3 = 0 is to be solved numerically starting with an initial guess as x0 = 2. The new estimate of x after the first iteration using Newton-Raphson method is ______. [2018 : 1 Mark, Set-II]
Ans: 1 to 1
Sol: Given
f(x) = 2x2 - 3x + 3, x0 = 2
f'(x) = 4x - 3
By Newton-Rapshon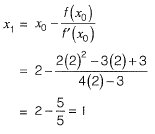
Q1: Consider the equation du/dt = 3t2 + 1 with u = 0 at t = 0. This is numerically solved by using the forward Euler method with a step size. Δt = 2. The absolute error in the solution in the end of the first time step is _____________. [2017 : 2 Marks, Set-I]
Ans: 7.95 to 8.05
Sol: du/dt = 3t2 + 1
f(u , f) = 3t2 + 1
u0 = 0
t0 = 0
Δt = 2
By Euler’s method
After first iteration u = 2 when t = 2
Absolute error = Exact value - approx value
= 10 -2
= 8
Q1: Newton-Raphson method is to be used to find foot of equation 3x - ex + sinx = 0. If the initial trail value of the roots is taken as 0.333, the next approximation for the root would be __________. [2016 : 1 Mark, Set-I]
Ans: 0.355 to 0.365
Sol: According to Newton-Raphson Method: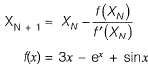
or, f' (x) = 3 - ex + cosx
⇒ 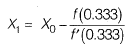
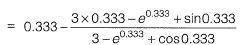
∴ X1 = 0.36
Q1: For step-size, Δx = 0.4, the value of following integral using Simpson’s 1/3 rule is _________. [2015 : 2 Marks, Set-II]
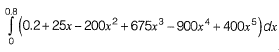
Ans: 1.36 to 1.37
Sol: a = 0,b = 0.8, Δx = 0.4
f{x) = 0.2 + 25x - 200x2 + 675x3 - 900x4 + 400x5
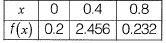
By Simpson’s 1/3 Rule
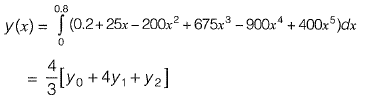
0 = y(0) = 0.2
y1 = y (0.4) = 2.456
y2 = y(0.8) = 0.232
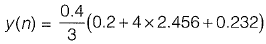
= 1.367
Q2: In Newton-Raphson iterative method, the initial guess value (xini) is considered as zero while finding the roots of the equation:
f(x) = -2 + 6x - 4X2 + 0.5.x3.
The correction, Δx, to be added to xini in the first iteration is ___________. [2015 : 1 Mark, Set-II]
Ans: 2.32 to 2.34
Sol: f (x) = - 2 + 6x - 4x2 + 0.5x3
f '(x) = 6 - 8x + 1 .5x2
xini = 0
By Newton Raphson Method,

⇒ 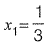
∴ 
Q3: The quadratic equation x2 - 4x + 4 = 0 is to be solved numerically, starting with the initial guess x0 = 3. The Newton-Raphson method is applied once to get a new estimate and then the Secant method is applied once using the initial guess and this new estimate. The estimated value of the root after the application of the Secant method is _____. [2015 : 2 Marks, Set-I]
Ans: 2.32 to 2.34
Sol: f(x) = x2 - 4x + 4
f'(x) = 2x - 4
x0 = 3
f (3) = 1, f'(3) = 2
By Newton Rapshon method,
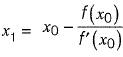
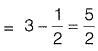
f(5/2) = 25/4 -10 + 4 = 1/4
By Secant method,
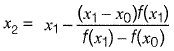
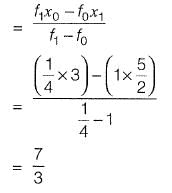
Q4: The integral 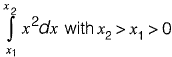 is evaluated analytically as well as numerically using a single application of the trapezoidal rule. If I is the exact value of the integral obtained analytically and J is the approximate value obtained using the trapezoidal rule, which of the following statements is correct about their relationship? [2015 : 1 Mark, Set-I]
is evaluated analytically as well as numerically using a single application of the trapezoidal rule. If I is the exact value of the integral obtained analytically and J is the approximate value obtained using the trapezoidal rule, which of the following statements is correct about their relationship? [2015 : 1 Mark, Set-I]
(a) J > I
(b) J < I
(c) J = I
(d) insufficient data to determine the relationship
Ans: (a)
Sol:
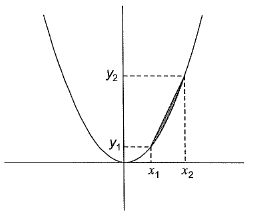
Exact value is computed by integration which follows thee exact shape of graph while computing the area.
Whereas, in Trapezoidal rule, the lines joining each points are considered straight lines which is not the exact variation of graph all the time like as shown in figure.
∴ J > I
OR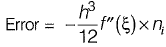
Here, f(x) = x2
or, f'(x) = 2x
or, f''(x) = 2 > 0
Since f''(x) is positive, the error is negative.
Since error = exact - approximate.
= I - J
and since error is negative in this case J > I is true.
Q1: The magnitude as the error (correct to two decimal places) in the estimation of following integral using simpson 1/3 rule. Take the step length as 1. [2013 : 2 Marks]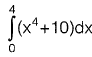
Sol: Using Simpson’s Rule,
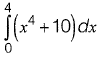
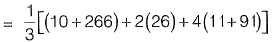
= 245.33
The value of integral,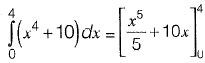
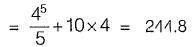
∴Magnitude of error = 245.33 - 244.8 = 0.53
Q1: The error in 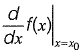 for a continuous function estimated with h = 0.03 using the central difference formula
for a continuous function estimated with h = 0.03 using the central difference formula 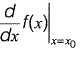
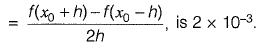 The values of x0 and f(x0) are 19.78 and 500.01, respectively. The corresponding error in the central difference estimate for h = 0.02 is approximately. [2011 : 2 Marks]
The values of x0 and f(x0) are 19.78 and 500.01, respectively. The corresponding error in the central difference estimate for h = 0.02 is approximately. [2011 : 2 Marks]
(a) 1.3 x 10-4
(b) 3.0 x 10-4
(c) 4.5 x 10-4
(d) 9.0 x 10-4
Ans: (d)
Sol: Error in central difference formula is 0(h2)
This means,
error ∝ h2
If error for h = 0.03 is 2 x 10-3 then,
Error for h = 0.02 is approximately
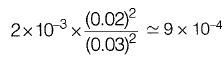
Q2: The estimate of  Obtained using Simpson's rule with three-point function evaluation exceeds the exact value by [2011 : 2 Marks]
Obtained using Simpson's rule with three-point function evaluation exceeds the exact value by [2011 : 2 Marks]
(a) 0.235
(b) 0.068
(c) 0.024
(d) 0.012
Ans: (d)
Sol: 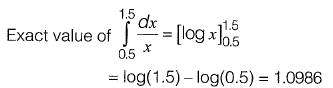
Approximate value by Simpson’s rule with 3 point is,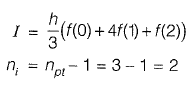
(npt is the number of pts and ni is the number of intervals)
Hero 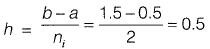
The tabic is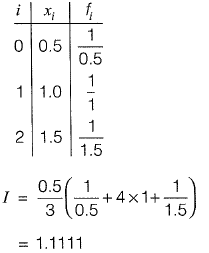
So the estimate exceeds the exact value by,
Approximate value - Exact value
= 0.012499
≈ 0.012
Q3: The square root of a number N is to be obtained by applying the Newton Raphson iterations to the equation x2 - N = 0. If i denotes the iteration index, the correct iterative scheme will be [2011 : 1 Mark]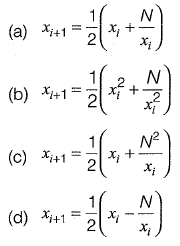
Ans: (a)
Sol: 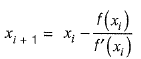
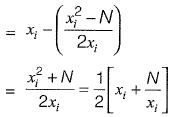
Q1: The table below gives values of a function F(x) obtained for values of x at intervals of 0.25.
The value of the integral of the function between the limits 0 to 1 using Simpson’s rule is [2010 : 2 Marks]
(a) 0.7854
(b) 2.3562
(c) 3.1416
(d) 7.5000
Ans: (a)
Sol: 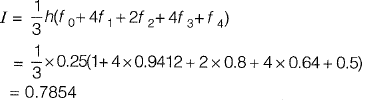
FAQs on Numerical Methods - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What are numerical methods and why are they important in solving mathematical problems? |  |
| 2. What are some common numerical methods used for solving differential equations? |  |
| 3. How do numerical methods differ from analytical methods? |  |
| 4. What role does error analysis play in numerical methods? |  |
| 5. Can numerical methods be applied to real-world problems, and if so, how? |  |





















