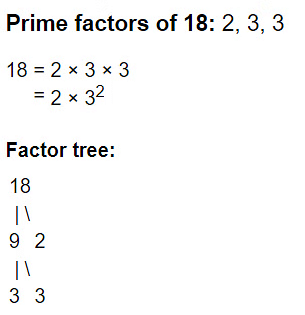Overview: HCF & LCM | CSAT Preparation - UPSC PDF Download
CSAT Angle
As per the CSAT point of view and the analysis of Previous Years’ Papers it has come to the notice that in the year 2025, two questions and in the years 2022-2016 one question each was asked from this chapter.
An analysis of previous years' papers highlights the significance of this topic, as at least one question is consistently asked from this chapter each year. Questions often involve calculating the LCM and its applications, such as determining the frequency of events occurring together. From an examination perspective, mastering this chapter is essential for aspirants. For instance, one question was asked in 2019, two in 2018, and 1-2 questions annually during the years 2017-2011.
The concept of HCF and LCM for a group of numbers depends on the fundamentals of factors and multiples. This concept of HCF and LCM is also useful for various other topic of basic numeracy. This chapter mainly deals with the calculation of HCF and LCM and their use and implementation in various problems.
Factors
Any composite number N, which can be expressed as
N = xa × yb × zc × ...
where, x , y and z are different prime factors of N and a , b, c are positive integers.
If a given number can be factorised upto its prime numbers, then these factors are called prime factors
e.g. 729 has factors 9 × 9 × 9 but 3 × 3 × 3 × 3 × 3 × 3 are prime factors of 729.
⇒ Total number of factors of N including 1 and number (N) itself
= (a + 1) (b + 1) (c + 1) . . .
e.g. 120 = 23 × 31 × 51
∴ Number of factors = (3 + 1) (1 + 1) (1 + 1) = 4 × 2 × 2 = 16
Multiples
The number X which can be completely divided by a number N is said to be the multiple of N .
e.g. Multiples of 5 are 10, 15, 20, 25 and 30 etc.
Common Multiple
A common multiple of two numbers is a number which is exactly divisible by each of the given numbers. e.g. 30 is a common multiple of 2, 3, 5 and 6.
Least Common Multiple (LCM)
The least common multiple of two or more given numbers is the least number which is exactly divisible by each one of them. e.g. 42 is the least common multiple of 2, 3 and 7. 84 is also the common multiple of 2, 3, 7 but 42 is the LCM of 2, 3, 7 as it is least among the two.
LCM of 4 and 6 via diagram is shown below:
Methods of Finding LCM
Methods of finding LCM are classified as:
1. By factorisation:
This method is further illustrated into following steps:
- Step 1 Find the standard form of the numbers.
- Step 2 Write out all the prime factors, which are contained in the standard forms of either of the numbers.
- Step 3 Raise each of the prime factors listed above to the highest of the powers in which it appears in the standard forms of the numbers.
- Step 4 The product of results of the previous step will be the LCM.
Example: The LCM of 8, 12 and 15 is
(a) 150
(b) 100
(c) 120
(d) 180
Ans: (c)
Sol: Step 1 Writing down the standard form of numbers
Factors of 8 = 2 × 2 × 2 = 23
Factors of 12 = 2 × 2 × 3 = 22 × 31
Factors of 15 = 3 × 5 = 31 × 51
Step 2 Writing down all the prime factors that appear atleast once in any of the numbers 2, 3, 5.
Step 3 Raise each of the prime factors to the highest available power (considering each of the numbers).
∴ LCM = 23 × 31 × 51 = 120
2. By division method:
In this method, the numbers are written together separated by commas and division is started with the least numbers which can atleast divide a number and further it is carried out to obtain the quotient of all number equal to one, then divisors are multiplied to obtain the LCM. The least common multiple of two or more given numbers is the least number which is exactly divisible by each one of them. e.g. 42 is the common multiple of 2, 3 and 7.
- Start division with the least digit and then further proceed to higher digits.
- Before calculating LCM or HCF, make sure that all numbers are in the same unit.
Example : Find the L.C.M. of 72, 240, 196.
Sol: (i) Using Prime Factorisation method:
⇨ 72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
⇨ 240 = 2 × 2 × 2 × 2 × 3 × 5 = 24 × 3 × 5
⇨ 196 = 2 × 2 × 7 × 7 = 22 × 72L.C.M. of the given numbers = Product of all the prime factors of each of the given number with greatest index of common prime factors
= 24 × 32 × 5 × 72 = 16 × 9 × 5 × 49 = 35280.(ii) Using the Division method:
2 | 72, 240, 196
2 | 36, 120, 98
2 | 18, 60 , 49
3 | 9 , 30 , 493 | 3 , 10 , 49
7 | 1 , 10 , 49
7 | 1 , 10 , 1
10 | 1 , 10 , 1
| 1 , 1 , 1
L.C.M. of the given numbers:
= Product of divisors and the remaining numbers
= 2 × 2 × 2 × 3 × 3 × 10 × 49
= 35280
Co-primes: Two numbers are said to be co-primes if their H.C.F. is 1.
Applications of LCM
- If some bells ring after different time interval, then time after which they will ring together = LCM of the different time interval.
- If some boys/men runs around a circular path taking different time, then time after which they meet at a point = LCM of different time taken by them.
Example: Three runners running around a circular track can complete one revolution in 2, 4 and 5.5 h, respectively. When will they meet at starting point?
(a) 40 h
(b) 44 h
(c) 20 h
(d) 22 h
Ans: (b)
Sol: Time at which they meet at starting point = LCM of 2, 4 and 5.5 = 44 h
Common Factor
A common factor of two or more numbers is a number which divides each of them exactly. e.g. 2 is the common factor of 2, 10 and 18.
Highest Common Factor (HCF)
The highest common factor of two or more numbers is the greatest number which divides each of them exactly. e.g. HCF of the numbers 18 and 24 is 6. It is also known as Greatest Common Divisor (GCD).
Methods of Finding HCF
There are basically three methods of finding out the HCF of a number
1. Factorisation Method
2. Division Method
3. Prime Factorisation
We will discuss the methods below:
1. Factorization Method
Express each number as the product of primes and take the product of the least powers of common factors to get the H.C.F.
Steps to solve:
- Step 1: Write each number as a product of its prime factors. This method is called here prime factorization.
- Step 2: Now list the common factors of both the numbers
- Step 3: The product of all common prime factors is the HCF ( use the lower power of each common factor).
Example: Evaluate the HCF of 60 and 75.
Sol: Write each number as a product of its prime factors.
22 x 3 x 5 = 60
3 x 52 = 75
The product of all common prime factors is the HCF.
The common prime factors in this example are 3 & 5.
The lowest power of 3 is 3 and 5 is 5.
So, HCF = 3 x 5 = 15
2. Division Method
- Step 1: Take the smaller number as the divisor and the larger number as a dividend.
- Step 2: Perform division. If you get the remainder as 0, then the divisor is the HCF of the given numbers.
- Step 3: If you get a remainder other than 0 then take the remainder as the new divisor and the previous divisor as the new dividend.
Example: Find out the HCF of 36 and 48.
Sol: Step I:Here we need to divide 48 by 36. ie. Dividend = 48 and Divisor = 36
[Divide the larger number by the smaller one].
Step II: Divide the 2 numbersStep III: When 12 becomes divisor, remainder becomes 0. Therefore, highest common factor = 12.
[The last divisor is the required highest common factor (H.C.F) of the given numbers].
3. Prime Factorization (Factor Tree) Method
Prime factorization is the process of breaking down a composite number into its prime factors, which are the prime numbers that multiply together to give the original number.
Steps to solve:
- Step 1: In calculating the HCF by prime factorization, we factorize the numbers into prime numbers, which are known as the prime factors.
- Step 2: Start by dividing the given numbers by 2(the first prime number), and go on dividing till you can’t divide the number any further.
- Step 3: Finally, then write the numbers as a product of the prime numbers. The product of these common factors is the highest common factor of the given numbers.
Example: Using the prime factorization method, find HCF of 18 and 90
Sol:
- Prime factorization of 18 is given below:
- Prime factorization of 90 is given below:
- There are 6 common factors of 18 and 90, that are 1, 2, 3, 6, 9, and 18. Therefore, the greatest common factor of 18 and 90 is 18.
Properties of LCM and HCF
Properties of LCM and HCF are define as follows:
- Property 1 The least number which is exactly divisible by a , b and c is the LCM of a , b and c.
- Property 2 The greatest number that will divide a , b and c is the HCF of a , b and c.
- Property 3 HCF of given numbers must be a factor of their LCM.
Relationship between HCF and LCM
Let us assume a and b are the two numbers, then the formula that expresses the relationship between their LCM and HCF is given as:
Product of Two numbers = (HCF of the two numbers) x (LCM of the two numbers) GCD (P, Q) × LCM (P, Q) = P × Q |
Note: This rule is applicable only for two numbers.
H.C.F. and L.C.M. of Decimals
In given numbers, make the same number of decimal places by annexing zeros in some numbers, if necessary. Considering these numbers without a decimal point, find H.C.F. or L.C.M. as the case may be. Now, in the result, mark off as many decimal places as are there in each of the given numbers.
- Step I: Convert each of the decimals to like decimals.
- Step II: Remove the decimal point and find the highest common factor and least common multiple as usual.
- Step III: In the answer (highest common factor /least common multiple), put the decimal point as there are a number of decimal places in the like decimals.
Example: Find the HCF and LCM of 3, 2.7, 0.09
Sol: Step-1: Write all the numbers with same number of digits after decimal point.
3.00, 2.70, 0.09Step-2: Now count the number of digits after decimal point (value is 2 for above problem) and calculate 10 power of the obtained value. Let the number be n = 102 = 100.
Step-3: Now remove the decimal point and find the LCM and HCF of the numbers.
LCM(300, 270, 9) and HCF(300, 270, 9).
- 300 = 22 x 31 x 52
270 = 21 x 33 x 51
9 = 20 x 32 x 50
LCM(300, 270, 9) = 22 x 33 x 52 = 2700
HCF(300, 270, 9) = 20 x 31 x 50 = 3
For finding the LCM and HCF, we should write the number in the power of prime numbers as written above. We should ensure that all the numbers should be written as power of prime numbers of same number. Example : 9 can be written as 32 but the other two numbers also contain 2 and 5 as primes. So we can write other two numbers as powers of 0. So 9 can be written as 20 x 32 x 50 and it won’t change the value of the number. Since we have our numbers in form of power of primes, Now the LCM is the number formed as the product of primes with its power is maximum value of the power of the same prime in given numbers.LCM = 2 power of max(2, 1, 0) x 3 power of max(1, 3, 2) x 5 power of max(2, 1, 0) = 22 x 33 x 52 = 2700 .
HCF calculation is similar but with only one change. Instead of taking max in power we take min in power.HCF = 2 power of min(2, 1, 0) x 3 power of min(1, 3, 2) x 5 power of min(2, 1, 0) = 20 x 31 x 50 = 3
Step-4: Now divide the obtained answer with our number n in step 2. The value we obtain is our required answer.
LCM(3, 2.7, 9) = 2700/100 = 27
HCF(3, 2.7, 9) = 3/100 = 0.03
H.C.F. and L.C.M. of Fractions
To calculate the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of fractions, find the HCF and LCM of their numerators and denominators separately.
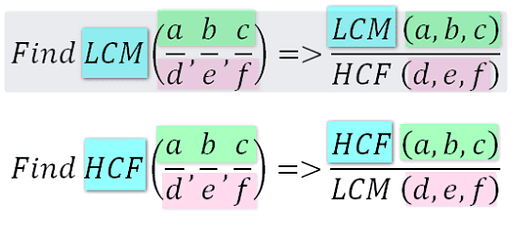
(a) HCF: To calculate the Highest Common Factor (HCF) of fractions, find the HCF of their numerators and denominators individually.
With fractions 3/6 and 5/15, the HCF of the numerators (3 and 5) is 1, and the HCF of the denominators (6 and 15) is 3. Thus, the HCF of the fractions is 1/3.
(b) LCM: To calculate the Lowest Common Multiple (LCM) of fractions, determine the LCM of their numerators and denominators separately.
The LCM of the numerators (3 and 5) is 15, and the LCM of the denominators (6 and 15) is 30. Consequently, the LCM of the fractions is 15/30, which simplifies to 1/2.
HCF and LCM of Polynomials
There are HCF and LCM of polynomials as given below:
- HCF of polynomials HCF of the polynomials is a common factor in all polynomials.
- LCM of polynomials LCM of polynomials is the least polynomial, which is divisible by each polynomial.
Common Applications of HCF and LCM
- The greatest number which divides the numbers x, y and z leaving remainders a, b and c, respectively = HCF of ( x − a ), ( y − b), ( z − c).
- The greatest number that will divide x, y and z leaving the same remainder in each case, is given by [HCF of ( x − y ), ( y − z ),( z − x ),... ] or [HCF of ( y − x ), ( z − y ), ( z − x ), ... ]
- The least number which when divided by x, y and z leaves the remainder a, b and c, respectively = [LCM of ( x , y , z )] − k
where, k = (x − a) = ( y − b) = (z − c) - The least number which when divided by x, y and z leaves the same remainder k in each case, is given by [LCM of ( x , y , z ) + k].
Solved Examples
Example1: There are three springs S1, S2 and S3, which are stretched and let go. Each spring is 100% elastic and comes to its original position every time after a fixed interval. S1 comes back to its original position in 72s . Similarily, S2 and S3 come back to their original position in 84 and 96s, respectively. When will they come back together for the second time?
(a) 
(b) 
(c) 60 min
(d) 66 min
Ans: (b)
Sol: Here, S1, S2 and S3 come back to their original position in 72, 84 and 96 s, respectively.
So, they will together come back to their original position at every instance that is a multiple of the LCM of their time i.e. the LCM of 72, 84 and 96.
Now, 72 = 23 × 32 84 = 22 × 31 × 71 and 96 = 25 × 31
∴ LCM of 72, 84 and 96 = 25 × 32 × 71 = 2016
Thus, the three springs will come back together every 2016 s.
∴ Hence, they will come back together for the second time after
2016 × 2 = 4032 s
=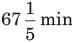
Example2: What is the LCM of 36, 48, 64 and 72?
(a) 576
(b) 476
(c) 572
(d) 540
Ans: (a)
Sol: LCM of 36, 48, 64 and 72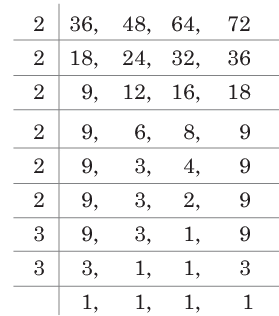
∴ LCM = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 = 576
Example3: Three bells ring at intervals of 9, 12 and 15 min, respectively. All the three begin to ring at 8 : 00 am. At what time will they ring together again?
(a) 8 : 45 am
(b) 10 : 30 am
(c) 11 : 00 am
(d) 1 : 30 pm
Ans: (c)
Sol: Since, the three bells ring at an interval of 9, 12 and 15 min, respectively.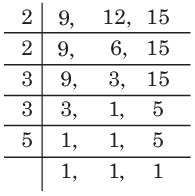
Then, time after which they ring together = LCM of (9, 12, 15)
∵ LCM = 2× 2× 3× 3× 5= 180min = 3h
∴ Hence, bells will ring together at (8 + 3) = 11 :00 am.
Example4: Find the HCF of 284 and 320 by long division method.
(a) 10
(b) 4
(c) 32
(d) 16
Ans: (b)
Sol: Divide 320 by 284,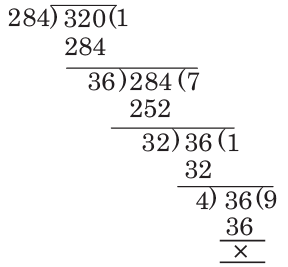
Hence, 4 is the HCF.
|
205 videos|265 docs|136 tests
|
FAQs on Overview: HCF & LCM - CSAT Preparation - UPSC
| 1. What is the difference between factors and multiples? |  |
| 2. How can the Least Common Multiple (LCM) be applied in real-life situations? |  |
| 3. What are some properties of LCM and HCF that are important to remember? |  |
| 4. How do you find the HCF and LCM of polynomials? |  |
| 5. What are common applications of HCF and LCM in competitive exams like UPSC? |  |