Overview: Light - Reflection & Refraction - 2 | Physics for Class 10 PDF Download
23. Absolute refractive index n of a given medium is defined as:
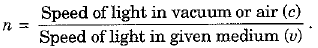
24. Refractive index is a unitless term. Moreover, absolute refractive index of a medium has a value equal to one or greater than one.
25. It is found that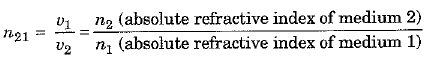
For a given wavelength and pair of media, n21 is a constant whose value depends only upon the optical properties of the two media and is independent of the angle of incidence.
26. A medium with larger refractive index is called optically denser medium and the medium with lesser refractive index is called optically rarer medium.
27. A ray of light travelling from a rarer medium to a denser medium bends towards the normal (i.e., ∠r < ∠i). However, a ray of light travelling from a denser to a rarer medium bends away from the normal (i.e.,∠r > ∠i).
28. Refractive index of air is generally taken as 1. Refractive index of water w.r.t. air is 1.33 and that of crown glass w.r.t. air is 1.52. Refractive index of diamond is maximum equal to 2.42.
29. Whenever a light ray suffers refraction through a glass slab of constant width, the emergent ray is parallel to the incident ray along the original direction. However, the emergent ray suffers a finite lateral displacement.
30. A lens is a part of a transparent material either bound by two spherical surfaces or bound by one plane and the other spherical surface. A lens is convex if it is thick in the middle and thin at edges. On the other hand, a concave lens is thin in the middle and thick at edges.
31. A convex lens converges the incident fight beam and is, thus, known as a converging (or convergent) lens. A concave lens diverges the incident fight beam and is known as a diverging (or divergent) lens.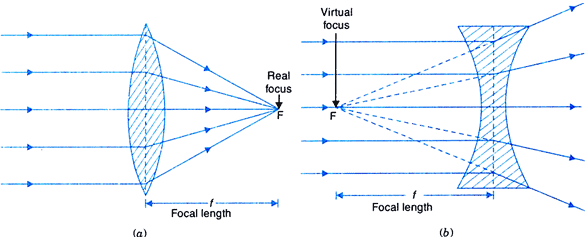 (a) Convex Lens; (b) Concave Lens
(a) Convex Lens; (b) Concave Lens
32. As a lens has two surfaces, each surface has its own centre of curvature. A straight fine passing through the two centres of curvature of a lens is called its principal axis.
33. The optical centre of a lens is the point on its principal axis, a ray of light passing through which goes undeviated. Generally, mid-point of a lens behaves as its optical centre.
34. The effective diameter of the circular outline of a spherical lens is called its “aperture”. For a thin lens aperture of lens is generally much less than its radius of curvature.
35. The principal focus of a lens is the point on its principal axis where a beam of light incident parallel to its principal axis actually converges to (in case of a convex lens) or appears to diverge from (in case of a concave lens) after refraction from the lens. A lens has two principal foci F1 and F2, one on each side of the lens.
The distance of the principal focus from the optical centre of a lens is called its focal length (f).
36. The position of the image formed by a lens can be found by considering any two of the following rays :
(i) A ray incident parallel to the principal axis, after refraction, passes through the principal focus on other side of lens in a convex lens or appears to diverge from the principal focus located on the same side of a concave lens.
(ii) A ray of light passing through the principal focus in a convex lens or appearing to meet at the principal focus in a concave lens emerges parallel to the principal axis after refraction.
(iii) A ray of light passing through the optical centre of lens emerges without suffering any deviation after refraction.
37. A convex lens can form a real or a virtual image depending upon the position of a real object. The different possibilities are as given in the following table 10.2.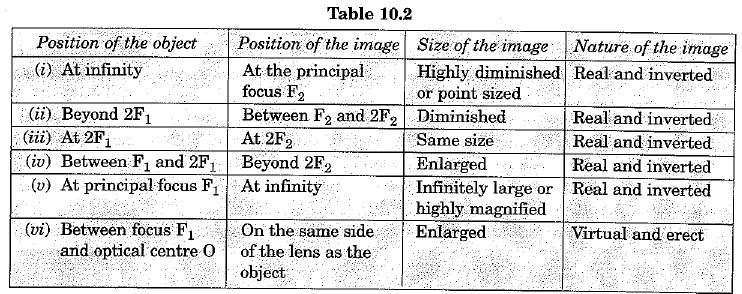
38. For a real object a concave lens always forms a virtual, erect and diminished image. For an object situated at infinity the point sized image is formed at the principal focus F1. In all other cases the diminished image is formed on the same side of the lens, as the object, between optical centre 0 and principal focus F1.
39. In dealing with lenses we use the same Cartesian Sign Convention as followed for mirror except that now all the distances are measured from the optical centre of the lens.
40. Lens formula is a relation correlating u, v and f for a lens. According to lens formula, we have :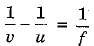
The relation is true for all lenses and all types of images formed. However, appropriate sign convention must be followed for u, v and f.
41. The magnification (m.) produced by a lens is given by

Magnification of a lens is -ve for a real and inverted image but +ve for a virtual and erect image.
42. The power (P) of a lens is a measure of the degree of convergence or divergence of light rays achieved by it. Mathematically, power of a lens is defined as the reciprocal of its focal length (f)
Thus, P = 1/f
SI unit of power is dioptre (D), where 1 D = 1 m-1. The power o f a convex (converging) lens is positive and that of a concave (diverging) lens is negative.
43. If a number of thin lenses having powers P1, P2, P3, ... are placed in contact then the net power (P) of the lens combination is equal to the algebraic sum of the individual powers i.e.,
P = P1 + P2 + P3,.....
|
23 videos|67 docs|58 tests
|
FAQs on Overview: Light - Reflection & Refraction - 2 - Physics for Class 10
| 1. What is the law of reflection? |  |
| 2. How does refraction occur? |  |
| 3. What is the difference between reflection and refraction? |  |
| 4. How does a concave mirror form an image? |  |
| 5. What is the speed of light in different mediums? |  |

|
Explore Courses for Class 10 exam
|

|

















