Parallel and Intersecting Lines Class 7 Notes Maths Chapter 5 Free PDF
In this chapter, we will explore the fascinating relationship between lines when they are drawn on a flat surface, like a piece of paper, a table top, or a blackboard. Think about the lines you see around you. Some lines cross each other, while others seem to run alongside each other forever without touching.
We will learn the special names for these lines and discover some interesting properties about the angles they form.
Across the Line
- Imagine taking a square piece of paper and folding it in different ways.
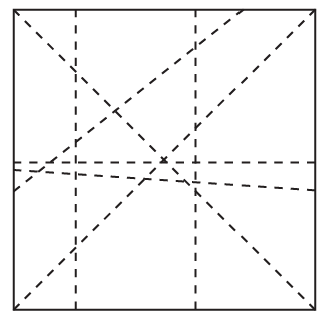
- If you draw lines along the creases, you'll notice various lines on the paper. What happens if you look at any two of these lines? Do they cross each other? If they don't cross on the paper, would they meet if you could extend them infinitely?
When two lines meet or cross each other at a single point on a flat surface, we say they intersect. The point where they cross is called the point of intersection.
Let's look closer at what happens when two lines intersect. Consider line l intersecting line m as shown below: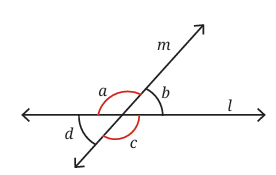
How many angles are formed at the point of intersection?
We can see four angles, labeled a, b, c, and d.
Thinking about the Angles:
Look back at Figure above . If we know the measure of one angle, say ∠a = 120°, can we figure out the measures of the other angles without measuring?
Angles ∠a and ∠b form a straight line together. A straight angle measures 180°. So, ∠a + ∠b = 180°. If ∠a = 120°, then ∠b must be 180° - 120° = 60°.
Similarly, ∠b and ∠c also form a straight line. So, ∠b + ∠c = 180°. If ∠b = 60°, then ∠c must be 180° - 60° = 120°.
And, ∠c and ∠d form a straight line. So, ∠c + ∠d = 180°. If ∠c = 120°, then ∠d must be 180° - 120° = 60°.
Notice something interesting? ∠a = ∠c = 120° and ∠b = ∠d = 60°.
The angles opposite each other at the intersection point are equal!
Key Concepts:
Linear Pair: Adjacent angles formed by two intersecting lines that add up to 180° (like ∠a and ∠b, or ∠b and ∠c). They form a straight line together.
Vertically Opposite Angles: Angles that are opposite each other when two lines intersect (like ∠a and ∠c, or ∠b and ∠d). Vertically opposite angles are always equal to each other. This is a fundamental concept, a proof in mathematics!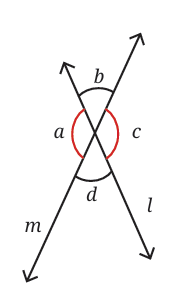

Perpendicular Lines

If all four angles are equal and they form a complete circle (360°), what would each angle measure?
That's right, each angle would be 360° / 4 = 90°.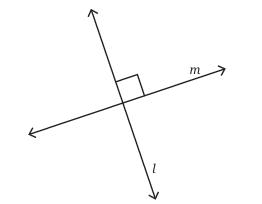
Perpendicular Lines: A pair of lines that intersect each other at a perfect right angle (90°). We use a small square symbol at the intersection to show that lines are perpendicular.
In the figure above, lines l and m are perpendicular to each other.
Between Lines
Let's look at different ways lines can relate to each other. Observe the line segments in the figure below.
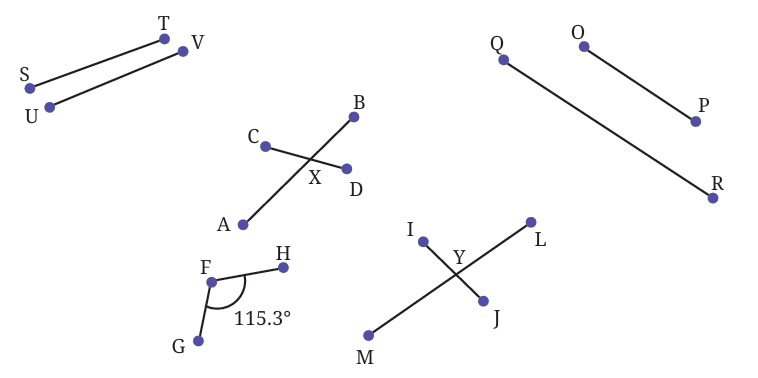
Some lines meet or intersect (like FG and FH meeting at F). But what about lines ST and UV? Or OP and QR? If you imagine extending them forever, would they ever meet?
Here are some examples of lines we notice around us.
These lines seem to run alongside each other, always keeping the same distance apart, and never intersecting. These are called parallel lines.
Parallel Lines: A pair of lines on the same flat surface (plane) that never meet or intersect, no matter how far they are extended in either direction.
Can you spot some parallel lines in your classroom or home?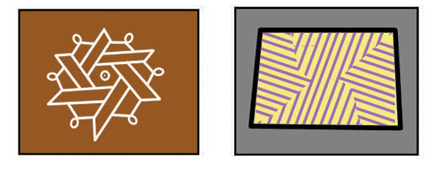
Parallel lines are often used in art and design, like for shading.
Parallel and Perpendicular Lines in Paper Folding
Let's explore parallel and perpendicular lines using a fun paper folding activity!
Activity: Folding Fun
Grab a plain square sheet of paper (newspaper works well!).
- Edges: Look at the opposite edges of the square.
How would you describe them?
They are parallel to each other. Now look at the adjacent edges (edges next to each other).
How do they relate?
They are perpendicular to each other, meeting at right angles (corners).
First Fold: Fold the sheet horizontally exactly in half. You've created a new line (crease) in the middle.
How many parallel lines do you see now?
(You should see the original top/bottom edges and the new middle crease - 3 parallel lines).
How does this new crease relate to the vertical sides of the original square?
It is perpendicular to them.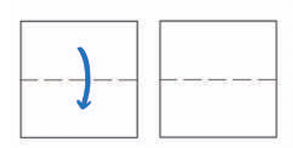
More Folds: Make another horizontal fold in the already folded sheet.
How many parallel lines now?
You should have 5.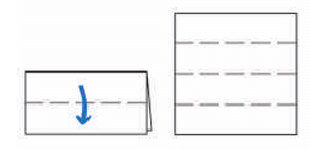 What if you fold it horizontally again?
What if you fold it horizontally again?
You'd get 9
Do you see a pattern?
Each fold adds more parallel lines
Vertical Fold: Now, unfold the paper back to the original square. Make a vertical fold down the middle. How does this new vertical line relate to the horizontal lines you made earlier?
It is perpendicular to them.
Diagonal Fold: Fold the sheet along a diagonal (corner to opposite corner).
Can you make another fold that creates a line parallel to this diagonal?
Answer: No, you cannot make a fold that is truly parallel to a diagonal using standard folding techniques — that is, by folding corner to corner or edge to edge.
Notations
How do we show lines are parallel or perpendicular in diagrams without writing it out every time?
Parallel Lines: We use arrow marks (>) on the lines. If there's more than one set of parallel lines, we use double arrows (>>), then triple arrows (>>>), and so on, for each different set.
Perpendicular Lines: We draw a small square symbol at the point of intersection where the right angle (90°) is formed.
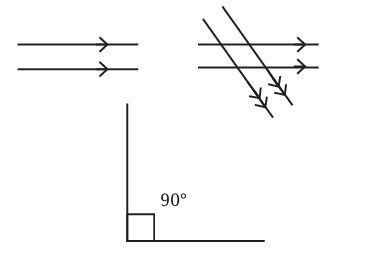 Representation of Parallel and Perpendicular Lines
Representation of Parallel and Perpendicular Lines
Transversals
Imagine a road crossing two or more parallel railway tracks. That road acts like a transversal.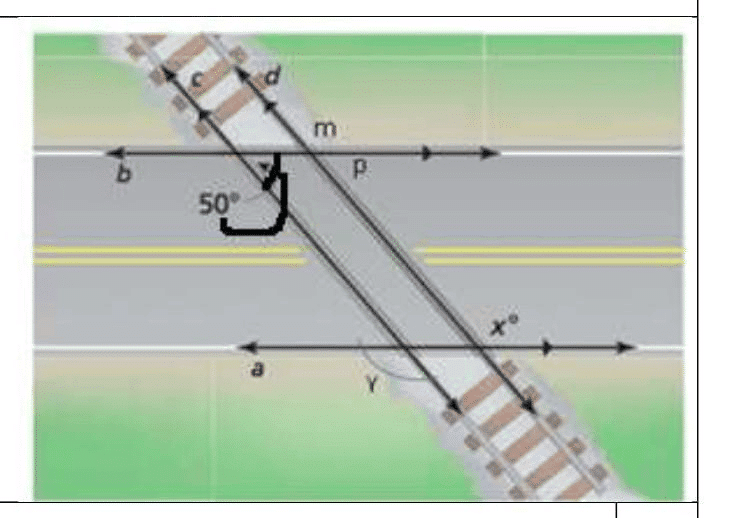
Transversal: A line that intersects (crosses) two or more other lines (which may or may not be parallel) at distinct points.
Let's look at line t crossing lines l and m:
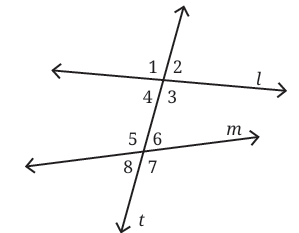
When a transversal cuts two lines, it creates several angles. These angles have special names based on their positions:
Types of Angles Formed by a Transversal:
1. Interior Angles: Angles that lie between the two lines l and m. (In Fig: ∠3, ∠4, ∠5, ∠6)
2. Exterior Angles: Angles that lie outside the two lines l and m. (In Fig: ∠1, ∠2, ∠7, ∠8)
3. Pairs of Corresponding Angles: Angles that are in the same relative position at each intersection point. Think of them as being in the "same corner". (Pairs: (∠1, ∠5), (∠2, ∠6), (∠3, ∠7), (∠4, ∠8))
4. Pairs of Alternate Interior Angles: Angles that are between the two lines but on opposite sides of the transversal. (Pairs: (∠3, ∠5), (∠4, ∠6))
5. Pairs of Alternate Exterior Angles: Angles that are outside the two lines and on opposite sides of the transversal. (Pairs: (∠2, ∠8), (∠1, ∠7))
6. Pairs of Interior Angles on the Same Side of the Transversal: Angles that are between the two lines and on the same side of the transversal. (Pairs: (∠3, ∠5), (∠4, ∠6)). These are sometimes called consecutive interior angles or co-interior angles.
Corresponding Angles
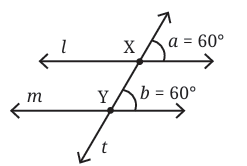 1. Corresponding Angles are Equal: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal. (e.g., ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8)
1. Corresponding Angles are Equal: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal. (e.g., ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8)
Converse is also true: If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel.
2. Alternate Interior Angles are Equal: If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal. (e.g., ∠3 = ∠6, ∠4 = ∠5)
Converse is also true: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
3. Interior Angles on the Same Side are Supplementary: If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary (they add up to 180°). (e.g., ∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°)
Converse is also true: If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Drawing Parallel Lines
Parallel lines are two lines that never meet, no matter how long you extend them. They are always the same distance apart.
Let's draw a pair of parallel lines using a ruler and a set square.
Tools You Need:
Ruler
Set square (a triangle-shaped tool with right angles)
Steps:
Step 1: Draw a line l using a ruler.
This line will be our reference or base line.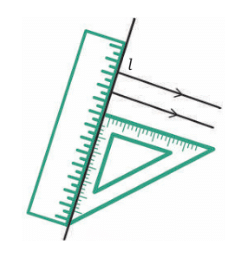
Step 2: Use your set square to draw a perpendicular line to l.
Place the set square so that one of its sides is touching line l and forms a 90° angle. Now draw a line along the other side of the set square.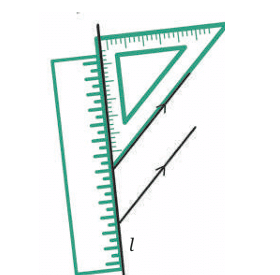
Step 3: Slide the set square.
Keep the ruler still and carefully slide the set square up or down while keeping the same angle. Draw a new line the same way.
Now you've drawn two lines that are both perpendicular to the same line (line l).
Are These Lines Parallel?
Yes! Here’s why:
You used the set square to ensure both lines made 90° angles with the same line (line l).
When a line cuts two other lines and makes equal corresponding angles (in this case 90°), the two lines must be parallel.
This is a rule in geometry:
If corresponding angles are equal, the lines are parallel.
Making Parallel Lines through Paper Folding
Imagine you have a piece of paper with a crease (fold) line labeled as line l. You are also given a point A not on this line. Your task is to draw a line through A that is parallel to l using only folds.
First Fold (Perpendicular to line l through A):
Fold the paper so that the crease you make is perpendicular to line l, and it passes through point A.
Call this new line t.
Second Fold (Perpendicular to t through A):
Now fold the paper again, but this time make the crease perpendicular to line t, and ensure it passes through A again.
Call this new crease m.
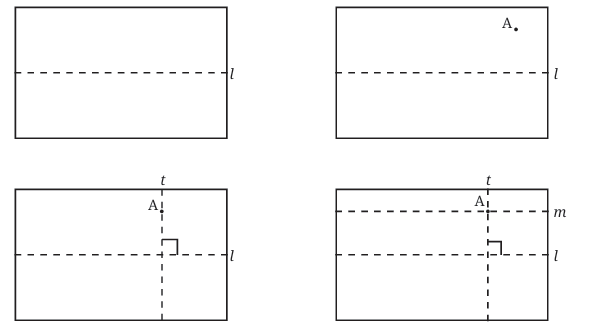
Since m is perpendicular to t, and t is perpendicular to l, the new line m is parallel to l.
Why This Works:
This is because two lines that are both perpendicular to the same line are always parallel to each other.
Alternate Angles
We have two lines l and m cut by a third line t (this third line is called a transversal).
Look at the diagram with angles a, b, c, d, e, f, g, h.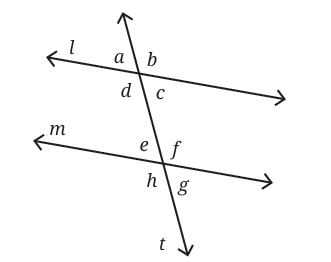
Alternate angles are on opposite sides of the transversal but between the two lines.
Example: ∠f and ∠d are alternate angles. Similarly, ∠e and ∠c are alternate angles.
Rule:
If the two lines are parallel, then alternate angles are equal.
If ∠f = 120°, then:
∠b = 120° (corresponding angle)
∠d = 120° (vertically opposite angle of ∠b)
So, ∠f = ∠d → which proves they are alternate angles and equal.
This proves lines l and m must be parallel if alternate angles are equal.
Summary:

Parallel Illusions
A parallel illusion happens when your eyes and brain are tricked into thinking lines are not parallel, even though they actually are!
In the picture, look carefully at all three designs.  At first, it looks like nothing is parallel, right?
At first, it looks like nothing is parallel, right?
But let’s find out what's really going on.
1. It looks like a burst of lines coming out from a center point.
At a glance, your brain thinks the lines are going in many directions, not parallel.
But guess what? → Some pairs of lines here are actually straight and parallel!
The radial design (lines from the center) makes your eyes focus on the middle, making it harder to see which lines are straight or equidistant.
2. This one is super tricky.
It looks like the black and white patterns are tilted or slanted.
But if you focus only on the horizontal black lines, you’ll notice: → They are actually all perfectly parallel!
The staircase or zig-zag shapes in between confuse your brain and create the illusion of a slope.
3. It seems like all the lines are curving or pointing in different directions.
But these lines are often used to trick your sense of depth (as if you're looking into a tunnel).
Some of these lines may be parallel, but because they are made to converge toward a center, it fools your eyes.
Why Do These Illusions Work?
Illusions like these work because of how our brain processes patterns and space:
Distractions: Other shapes (like zigzags or curves) distract your eyes.
Angles: Sharp angles make you think lines are changing direction.
Context: Your brain compares lines to nearby objects.
Depth Perception: Some images make flat things look 3D (like the tunnel effect).
The straight lines start looking curved or tilted, even though you used a ruler!
Some Solved Examples
Q1: You look at an image that has horizontal black lines between zigzag patterns. The lines appear slanted. Are they actually slanted?
Sol: No. The lines are perfectly parallel, but the design around them creates an optical illusion that tricks your eyes.
Q2: Two angles form a straight line. One angle measures 122°. What is the other?
Sol: Angles on a straight line add up to 180° (linear pair).
So,
180° − 122° = 58°
Q3: A transversal crosses two lines. Angles on opposite sides of the transversal between the lines are alternate interior angles. One angle is 65°. What is the other?
Sol: If the lines are parallel, then alternate interior angles are equal.
So the other angle is also 65°.
FAQs on Parallel and Intersecting Lines Class 7 Notes Maths Chapter 5 Free PDF
| 1. What are the characteristics of perpendicular lines? |  |
| 2. How can I identify parallel lines? |  |
| 3. What is a transversal line, and how does it interact with parallel lines? |  |
| 4. Can you explain the angles formed by a transversal with parallel lines? |  |
| 5. How can paper folding demonstrate the concepts of parallel and perpendicular lines? |  |

























