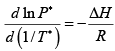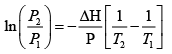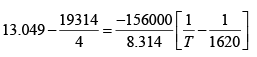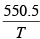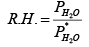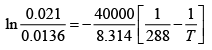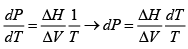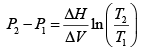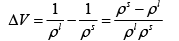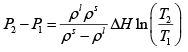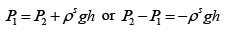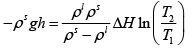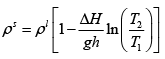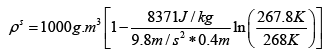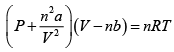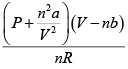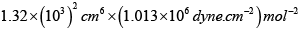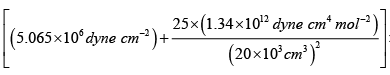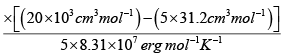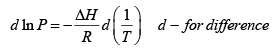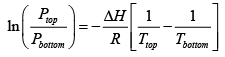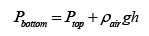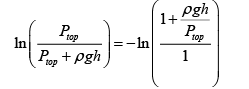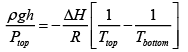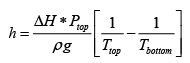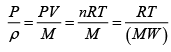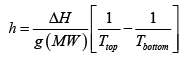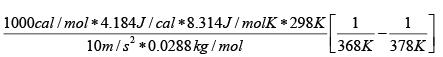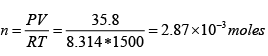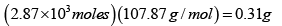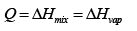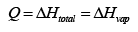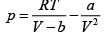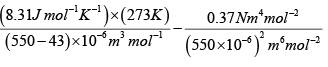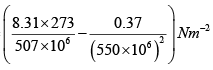Phase Transition: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q.1. The boiling point of Li is 1620K .
(a) What is the vapor pressure of liquid Li at 1000K ?
(b) Estimate the melting point of lithium from the data given.
Data:
Enthalpy of evaporation is 156 kj /mol
Vapour pressure above solid Li is given by: 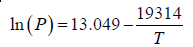
(a) Integrate the Clausius Clayperon Equation
(b) At the melting point of Li Psolid = Pliquid
1.47 =
T = 375K
Q.2. (a) What is the vapor pressure of H2O at 0 100oC boiling point of water)?
(b) The water forecast tells me that it is 59oF (15oC) outside with a relative humidity of 65%. What is the dew point of that air?
Data: Enthalpy of evaporation for 0
H2O100oC = 40.6kJ /mol
(a) The boiling point is where P* = Patomsphere .So P* H2O = 1atm at the regular boiling point.
(b) The Clausius-Clayperon equation allows us to find vapor pressure at some temperature from knowledge of the vapor pressure at another temperature
We can integrate this between 373K and 288K
= 0.021 atm
Relative humanity is defined as
In this problem the relative humanity is 65% so we can find the PH2O
= 0.0136 atm
The dew point is the temperature where PH2O = P*H2O. Again we integrate the Clausius- Clayperon equation, this time solving for T
T = 281K= 8oC
Q.3. A long vertical column is closed at the bottom and open at the top; it is partially filled with a particular liquid and cooled to -5oC . At this temperature the fluid solidifies below a particular level, remaining liquid above this level. If the temperature if further lowered to 0 -5.2oC the solid-liquid interface moves upward by 40cm . The latent heat (per unit mass) is 2cal / g and the density of the liquid phase is 1g / cm3 . Find the density of the solid phase. Neglect thermal expansion of all materials.
(Hint: Note that the pressure at the original position of the interface remains constant)
Once again, we start with me Clausius-Clayperon equations in this form
Integrating we get
Let P1 be the pressure at the original interface (T1 =-5oC ) and P2 be the pressure at the new interface (T2 =-5.2oC)
We can also relate the densities to the volume change as follows:
Also, we know
Putting this together we get
Solving for the density of the solid,
Putting in the values of the know quantities (being very careful with units)
ρs = 2.6g / cm3
Q.4. For a gas obeying van der Walls' equation, the constants are a =1.32litre2 atm. mol-2 and b = 3.12 x 102 litremol-1 . Calculate the temperature at which 5 moles of the gas at 5atmospheric pressures will occupy a volume of 20 litre. Given R = 8.31 x 107 ergmol- K-1
The van der Waals' equation for n moles of the gas is
By inverting it, we can write
T =
Here,
a = 1.32litre2 atm. mol-2
= 1.34x 10dyne cm4 mol-2
b = 3.12 x10-2 litre mol2
= 3.12 x 10-2cm3 mol1
= 3.12 cm3mol-1
p = 5 atm
= 5 x 1.013 x106 dyne cm-2
= 5.065 x106 dyne cm-2
V = 20 litre = 20 x103 cm3
n = 5, R = 8.31x107 erg mol-1 K-1
T =
= 245.9K
Q.5. It is found that a certain liquid boils at a temperature of 95oC at the top of a hill, whereas it bolls at a temperature of 105oC at the bottom. The latent heat is 1000 cal /mol. What is the approximately height of the hill?
There are two steps to solving this problem
(1) What is the pressure difference in terms of the height?
(2) What is the height of the hill?
Use the following from the Clayperon equation (this is valid for equilibrium between an ideal gas and a solid or liquid ΔH is latent Heat)
Which in this case can be written in terms of the pressure at the top and bottom of the hill, and the respective boiling points?
Now we write the pressure at the bottom in terms of the pressure at the top
Substituting this,
If we expand ln (1 + x ) we get,
Assuming that the air is an ideal gas, we can relate the density and pressure to the temperature using the ideal gas law
Where ( MW ) is the molecular weight of the air? We now have
Plugging in some numbers ( g = 10m/s2 , MW= 28.8g/mol and we dealing with air at 25oC
h =
h = 2.6km
Q.6. (a) A chamber at 1500K with a volume of one cubic meter contains one gram of Ag .
What is the status of the silver in the chamber? Is it all vapor, all liquid, or part liquid and part vapor? If the latter, what fraction of the silvers is in the vapor phase?
(b) How much heat is required to evaporate one mol of Ag from a very large quantity of a silver-copper liquid solution at 1500K containing xAg = 0.25 . Assume the solution is ideal.
Data for Silver:
Melting point =1235K
Vapor pressure of liquid given by
Enthalpy of melting for Ag =11.3kJ /mol
Heat capacity for liquid Ag = 33 J /mol - K
First we can find what the vapor pressure over the liquid would be under these conditions
= -7.95
P* = 3.54 x 10-4 atm = 35.8Pa
If all of the silver was in the vapor phase ( (1gram )
P =
= 115.61Pa
Hence, there must be both liquid and vapor present
P = P*= 35.8Pa
Now we can find the moles in the vapor phase
Game of vapor
So the fraction in the vapor phase is 0.31
(b) In general the amount of heat necessary would be the sum of the mixing enthalpy and the enthalpy of vaporization
However since we are told to assume the solution is ideal, the enthalpy of mixing is zero. (This is related to the assumption that the mixing species do not interact)
Thus
Since we were not given the enthalpy of vaporization or the boiling point in the data, we must find these quantities. To find the boiling point, use the given equation for the vapor pressure and find the temperature where the pressure is equal to 1 atm .
Choosing T = 1500 and 1600 K , the valued calculated for ΔHvap is 255 kg / mole . (If you this up you get 251 kJ / mole ) Now we can get enthalpy of vaporization at 1500K , which can be done using a loop, since we know enthalpy is a state function
ΔHvap (1500K )= 267kJ / mol
Q.7. The Vapor pressure of pure B at 1000K is 4 5 10 atm . If B is in an ideal solution with another species at 1000K , its vapor pressure will be:
Higher than 5 x 10-4
Lower than 5 x 10-4
Equal to 5 x 10-4
Impossible to say
The vapor pressure of pure B at 1000 K is 5 x10-4 atm . If B is in an ideal solution with another species at 1000 K , its vapor pressure will be:
Higher than 5 x10-4
Lower than 5 x10-4 is answer
Equal to 5 x10-4
Impossible to say
Q.8. One mole of a gas occupies a volume of 0.55 litres at 0oC . Calculate the pressure it will exert if it behaves as (a) an ideal gas and (b) as a van der Walls' gas.
Given a= 0.37 Nm4 mol-2 ,b = 43 x 106 m3 mol-1 and R = 8.31Jmol-1 K-1
Here V = 0.55 litre mol-1 = 550cm3mol-1 = 550 x 10-6 m3mol-1
(a) For one mole of an ideal gas,
P = RT/V
On substituting the values of various quantities, we get
p =
= 4.12 x106 Nm-2
(b) For one mole of van der Walls' gas,
=
=
= (0.48 x 106 -1.22 x 106) Nm-2
= 3.26 x 106Nm-2
As expected, the pressure exerted by a van der Waals' gas is less than that exerted by an ideal gas.
|
6 videos|20 docs|32 tests
|
FAQs on Phase Transition: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is a phase transition in the context of the IIT JAM exam? |  |
| 2. How can I identify if a phase transition has occurred during an experiment? |  |
| 3. What are the different types of phase transitions that can occur? |  |
| 4. Can phase transitions be reversible? |  |
| 5. How are phase transitions related to the IIT JAM exam syllabus? |  |