Polynomials & Zeroes of a linear Polynomial | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Introduction |

|
| Degree of a Polynomial |

|
| Arithmetic Operations |

|
| Properties of Polynomial |

|
| Zeroes of a Polynomial |

|
Introduction
- Polynomial is made up of two terms, namely Poly (meaning “many”) and Nomial (meaning “terms”).
- A polynomial is defined as an expression that is composed of variables, constants, and exponents, that are combined using mathematical operations such as addition, subtraction, multiplication, and division. (Division operation by a variable is not allowed).
- Polynomial is an algebraic expression, that has only the whole number powers of the variables.
- Variables: A variable is an entity whose value is not fixed; it can vary. Variables are generally denoted by the letters x, y, z etc.
- Constants: A constant is an entity whose value is fixed for the given situation. The value of the constant might be unknown, but we know that it is fixed. Constants are generally denoted by the letters a, b, c, p, q etc if their values are not known or not provided, and by specific numerical values (like 3, etc) if their values are known.
- In an expression, generally, we have variables and constant terms.
Example: 3x² + 2x + 6; Here x is variable and 6 without any variable is called constant. - The polynomial function is denoted by P(x) where x represents the variable.
Example: P(x) = x2 - 5x + 11; If the variable is denoted by a, then the function will be P(a) - The terms of polynomials are the parts of the equation that are generally separated by “+” or “-” signs. So, each part of a polynomial in an equation is a term.
Example: In a polynomial, say, 2x2 + 5x + 4, the number of terms will be 3.
What are the Terms?
- The parts of algebraic expressions that are separated by addition or subtraction are called terms.
- The number of terms decides the type of expression, whether it is a monomial, binomial, trinomial or polynomial.
- These terms are made of a product of variables and coefficients that are added together to form expressions. For example, 2x and 9 are added together to form the expression: 2x + 9.
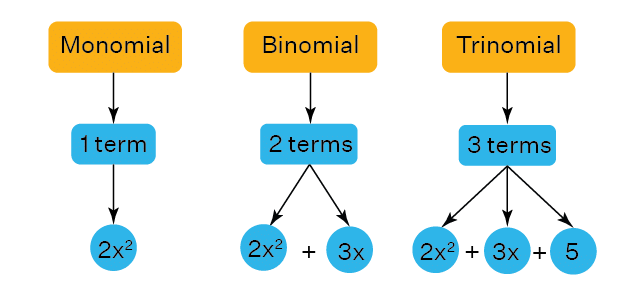 Types of algebraic Expression
Types of algebraic Expression
Monomial Polynomial
A monomial is an algebraic expression that has only one term.
Or we say a single term expression is a monomial.
The examples of monomials are: 12x, 12, -25x, 24y, 4a, xy
Binomial Polynomial
A binomial is an algebraic expression that has two unlike terms.
The examples of binomials are:
- x + y
- m – 5
- a2 – b2
- xy + 5
- 3p – 2q
Trinomial Polynomial
A trinomial is an algebraic expression that has three terms in it.
The examples of trinomials are:
- x + y + 7
- ab + a +b
- 3x 2 – 5x + 2
- m + n + 10
The expression x + y + 3x is not a trinomial as the terms x and 3x are like terms.
Polynomial in One Variable
- Polynomials in one variable are algebraic expressions that consist of one variable in it.
- Example: The following equation: x2+2x+4 is a polynomial in one variable. It only consists of one variable, x.
Degree of a Polynomial
- The degree of an algebraic equation is the highest degree for a term with a non-zero coefficient.
- The degree of a term is the sum of the powers of each variable in the term.
Examples:
(i) 4x7-5
In this expression, we have only one term with a variable and the power of the term is 7, so the expression has a degree, 7.
(ii) 5 x3y3 - 4 x2y2 + 7xy
Here, it has 3 terms, and the power of the first term is 3+3=6, the power of the second term is 2+2=4, and the power of the last term is 1+1=2, here the highest power is 6, so the expression has a degree, 3+3=6.
How to find the Degree of a Polynomial?
There are 5 simple steps present to find the degree of a polynomial:
Example: 3x2 - 3x4 - 5 + 2x + 2x2 - x
- Step 1: Combine like terms. Combine all of the like terms in the expression so you can simplify it if they are not combined already. Let's say you're working with the following expression: 3x2 - 3x4 - 5 + 2x + 2x2 - x. Just combine all of the x2, x4, x and constant terms of the expression to get 5x2 - 3x4 - 5 + x.
- Step 2: Drop all of the constants and coefficients. The constant terms are all of the terms that are not attached to a variable, such as 3 or 5. The coefficients are the terms that are attached to the variable. When you're looking for the degree of a polynomial, you can either just actively ignore these terms or cross them off. For instance, the coefficient of the term 5x2 would be 5. The degree is independent of the coefficients, so you don't need them. Working with the equation 5x2 - 3x4 - 5 + x, you would drop the constants and coefficients to get x2 - x4 + x.
- Step 3: Put the terms in decreasing order of their exponents. This is also called putting the polynomial in standard form. The term with the highest exponent should be first, and the term with the lowest exponent should be last. This will help you see which term has the exponent with the largest value. In the previous example, you would be left with
-x4 + x2 + x. - Step 4: Find the power of the largest term. The power is simply a number in the exponent. In the example, -x4 + x2 + x, the power of the first term is 4. Since you've arranged the polynomial to put the largest exponent first, that will be where you will find the largest term.
- Step 5: Identify this number as the degree of the polynomial. You can just write that the degree of the polynomial = 4, or you can write the answer in a more appropriate form: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 4. You're all done.
Based on the degree of a polynomial, the polynomials in one variable are classified as follows:
- Zero polynomial or constant polynomial
- Linear Polynomial
- Quadratic Polynomial
- Cubic Polynomial

1. Zero Polynomial or Constant Polynomial
If the degree of the polynomial is zero (0), then the polynomial is called zero or constant polynomial. Such kinds of polynomials have only constants. They don’t have variables.
The examples of constant polynomials are 2, 5, 7 and so on. Here, 2 can be written as 2x0, 5 can be written as 5x0, and so on.
2. Linear Polynomial
If the degree of the polynomial is 1 (one), then the polynomial is called a linear polynomial. The linear polynomial in one variable has only one solution.
Examples of linear polynomials in one variable are:
- m+2
- y+5
- x+10
3. Quadratic Polynomial
A polynomial with the highest degree of 2 is called a quadratic polynomial. A quadratic polynomial in one variable has only two solutions. Some of the examples of quadratic polynomials in one variable are:
- 9x2 – 10
- x2 +5x+9
- m2+25
4. Cubic Polynomial
If the highest exponent of a variable in a polynomial is 3 (i.e. degree of a polynomial is 3), then the polynomial is called a cubic polynomial. A cubic polynomial in one variable has exactly 3 solutions. The examples of a cubic polynomial in one variable are:
- 7x3– 21
- 8x3+2x+9
- 10m3 + (5/4)
Arithmetic Operations
 |
Download the notes
Polynomials & Zeroes of a linear Polynomial
|
Download as PDF |
1. Addition
For adding any two polynomials, we have to combine the like terms.
Example: Add 4 x² + 7 x - 6, x² - 3 x + 2
∵ Like terms are 4x² and x², 7x and -3x, -6 and 2
⇒ If we combine 4x² and x², we will get 5x²
⇒ If we combine 7x and -3x, we will get 4x
⇒ If we combine -6 and 2, we will get -4
Thus, the final answer is 5x² + 4x - 4.
2. Subtraction
(2 x³ - 2 x² + 4 x - 3) - (x³ + x² - 5 x + 4)
Step 1: Multiply the negative with inner terms i.e. 2x³ -2x² + 4x -3 - x³-x²+5x-4
Step 2: Combine the like terms i.e. 2x³ - x³ -2x²-x² + 4x + 5x - 3 - 4
Step 3: The answer i.e. x³ - 3x² + 9x - 7.
3. Multiplication
There are two formats for this: horizontal and vertical, like in addition.
The simplest case of the multiplication of polynomials is the multiplication of monomials.
Example: (5x²)(- 2x³)
For multiplying these two monomials, we have to just multiply the numbers and add the powers using the exponent rule.
⇒ (5x²)(-2x³) = -10x² ⁺ ³= -10x⁵
4. Division
The division of polynomials involves two cases, the first one is a simplification, which is reducing the fraction and the second one is a long division.
Properties of Polynomial
Some of the important properties of polynomials along with some important polynomial theorems are as follows:
(i) Division Algorithm
If a polynomial P(x) is divided by a polynomial G(x) results in quotient Q(x) with remainder R(x), then, P(x) = G(x) • Q(x) + R(x)
(ii) Bezout’s Theorem
Polynomial P(x) is divisible by binomial (x – a) if and only if P(a) = 0.
(iii) Factor Theorem
A polynomial P(x) divided by Q(x) results in R(x) with zero remainders if and only if Q(x) is a factor of P(x).
(iv) The addition, subtraction and multiplication of polynomials P and Q result in a polynomial where,
Degree(P ± Q) ≤ Degree(P or Q)
Degree(P × Q) = Degree(P) + Degree(Q)
(v) If P(x) = a0 + a1x + a2x2 + …… + anxn is a polynomial such that deg(P) = n ≥ 0 then, P has at most “n” distinct roots.
Zeroes of a Polynomial
The zeros of a polynomial p(x) are all the x-values that make the polynomial equal to zero.
Definition
Let p(x) be a polynomial in x. If p(a) = 0, then we say that 'a' is a zero of the polynomial p(x).
Zero of a Linear Polynomial
Example 1. Find the zeros of the following linear polynomial
p(x) = 2x + 3
Solution: p(x) = 2x + 3
Now we have to think about the value of x, for which the given function will become zero.
For that let us factor out 2
p(x) = 2 (x + 3/2)
Instead of "x", if we substitute -3/2, p(x) will become zero.
Hence -3/2 is the zero of the given linear polynomial.
Example 2. Find the zeros of the following linear polynomial
Consider, P(x) = 4x + 5 to be a linear polynomial in one variable.
Solution: Let ‘a’ be zero of P(x), then,
P(a) = 4a+5 = 0
Therefore, a = -5/4
In general, if k is zero of the linear polynomial in one variable: P(x) = ax +b, then;
P(k) = ak+b = 0
k = -b/a
It can also be written as,
Zero of Polynomial (K) = -(Constant/ Coefficient of x)
|
40 videos|419 docs|51 tests
|
FAQs on Polynomials & Zeroes of a linear Polynomial - Mathematics (Maths) Class 9
| 1. What is the degree of a polynomial? |  |
| 2. What are the arithmetic operations that can be performed on polynomials? |  |
| 3. What are the properties of polynomials? |  |
| 4. How do you find the zeroes of a polynomial? |  |
| 5. What are the zeroes of a linear polynomial? |  |


































