Practice Questions: A Tale of Three Intersecting Lines | Mathematics (Ganita Prakash) Class 7 - New NCERT PDF Download
Q1. In triangle LMN, if ∠L = 50° and ∠N = 80°, find the exterior angle at vertex M.
Sol:
First, find ∠M:
∠M = 180° - (50° + 80°) = 180° - 130° = 50°
The exterior angle at M is supplementary to ∠M:
Exterior angle = 180° - 50° = 130°
Q2. In triangle DEF, if ∠D = 90° and ∠E = 30°, what is the measure of ∠F?
Sol:
The sum of angles in a triangle is 180°.
∠F = 180° - (90° + 30°)
= 180° - 120°
= 60°
Q3. In triangle STU, if ∠S = 50° and ∠T = 75°, find ∠U and the ratio of angles S, T, and U.
Sol:
Find ∠U:
∠U = 180° - (50° + 75°) = 180° - 125° = 55°
Ratio of angles:
∠S : ∠T : ∠U = 50 : 75 : 55
Divide by greatest common divisor (5):
50 ÷ 5 = 10,
75 ÷ 5 = 15,
55 ÷ 5 = 11
Ratio = 10 : 15 : 11
Q4. In triangle PQR, if ∠P = 55° and ∠Q = 65°, find the exterior angle at vertex R and its relationship with ∠P and ∠Q.
Sol:
First, find ∠R:
∠R = 180° - (55° + 65°) = 180° - 120° = 60°
The exterior angle at R is supplementary to ∠R:
Exterior angle = 180° - 60° = 120°
Relationship: The exterior angle at R equals the sum of opposite interior angles ∠P and ∠Q:
55° + 65° = 120°
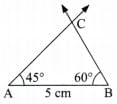
Q5. Construct triangles for the following measurements:
45°, 5 cm, and 60°
Sol:
Steps of Construction:
Step 1: Draw the base AB of length 5 cm.
Step 2: Draw ∠A and ∠B of measures 45° and 60° respectively.
Step 3: The point of intersection of the two new arms of ∠A and ∠B is the third vertex C.
Q6. Can a triangle have sidelengths 6 cm, 8 cm, and 10 cm?
Sol:
To form a triangle, the sum of the lengths of any two sides should be greater than the length of the third side.
So, 6 cm + 8 cm = 14 cm > 10 cm
8 cm + 10 cm = 18 cm > 6 cm
6 cm + 10 cm = 16 cm > 8 cm
Thus, a triangle is possible with side lengths 6 cm, 8 cm, and 10 cm.
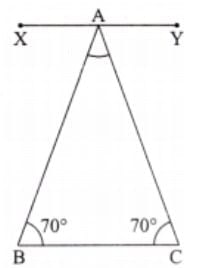
Q7. Can you construct a triangle all of whose angles are equal to 70°? If two of the angles are 70°, what would the third angle be? If all the angles in a triangle have to be equal, then what must its measure be? Explore and find out.
- Sol: No, it is not possible to construct a triangle with all angles equal to 70°, As
In any triangle, the sum of all three angles is always 180°.- If you try to make all three angles 70°, the total will be:
70° + 70° + 70° = 210°, which is more than 180°.- That’s not possible, so such a triangle cannot be made.
If we take two base angles as 70° that is, ∠B and ∠C = 70°, then we have to find ∠BAC.
Since XY is parallel to BC.
So, ∠XAB = ∠B = 70° ….. (i)
and ∠YAC = ∠C = 70° …… (ii)
Also, ∠XAB + ∠BAC + ∠YAC = 180°
⇒ 70° + ∠BAC + 70° = 180° [Using (i) and (ii)]
⇒ ∠BAC = 180° – 140° = 40°.
So, the third angle would be 40°.
If all the angles in a triangle have to be equal, then each angle must measure 60°. This type of triangle is called an equilateral triangle.
|
41 videos|251 docs|8 tests
|
FAQs on Practice Questions: A Tale of Three Intersecting Lines - Mathematics (Ganita Prakash) Class 7 - New NCERT
| 1. What are intersecting lines and how do they differ from parallel lines? |  |
| 2. How can the angles formed by intersecting lines be calculated? |  |
| 3. What is the significance of intersecting lines in geometry? |  |
| 4. Can you provide real-life examples where intersecting lines are observed? |  |
| 5. What are the types of angles formed by two intersecting lines? |  |