Class 7 Maths Chapter 1 Practice Question Answers - Rational Numbers
Q1. Between any two rational numbers,
(a) there is no rational number
(b) there is exactly one rational number
(c) there are infinitely many rational numbers
(d) there are only rational numbers and no irrational numbers
Ans: (c)
Sol: Recall that to find a rational number between r and s, you can add r and s and divide the sum by 2, that is r + s / 2 lies between r and s.
For example, 5/2 is a number between 2 and 3. We can proceed in this manner to find many more rational numbers between 2 and 3.
Hence, we can conclude that there are infinitely many rational numbers between any two given rational numbers.
Q2. Every rational number is
(a) A natural number
(b) An integer
(c) A real number
(d) A whole number
Ans: (c)
Sol:
Step-1: Explain property of rational numbers
A real number is a number which can be expressed in the form p/q , where q ≠ 0.
Step-2: Proving that every rational number is a real number
Real numbers are numbers that include bothe rational and irrational numbers.
Hence, every rational number is a real number.
Final Answer: Every rational number is a real number. The correct option is (C).
Q3. A number that can be expressed in the form a/b , where a and b are integers and b is not equal to zero is called
(a) a fraction
(b) an integer
(c) a rational number
(d) a real number
Ans: (c)
Sol: A rational number : A number that can be in the form of p/q, where p and q are integers and q is not equal to zero.
Q4. 5/8 - 2/8 = _________
(a) 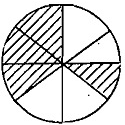
(b) 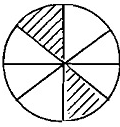
(c) 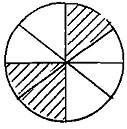
(d) 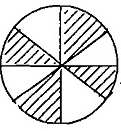
Ans: (c)
Sol: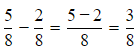
It was represented by
Q5. If p: every fraction is a rational number q: every rational number is a fractionthen which of the following is correct?
(a) p is true and q is false.
(b) p is false and q is true.
(c) Both p and q are true.
(d) Both p and q are false.
Ans: (a)
Sol: Fraction is defined as a part of a whole thing. Every fraction is of the form m/n where m is a whole number and n is a natural number.
Rational number is defined as the number of the form a/b
where a and b are integers and b ≠ 0.
Since all whole numbers and natural numbers are present in set of integers every fraction is a rational number.
So, the statement p is true.
But every rational number is not a fraction.
So, the statement q is false.
Q6.If we divide a positive integer by another positive integer, what is the resulting number ?
(a) Always a natural number
(b) Always an integer
(c) A rational number
(d) An irrational number
Ans: (c)
Sol: If we divide a positive integer by another positive integer, the resulting number is always a rational number.
Though it can be a natural number and an integer only if the denominator is 1.
Q7. -5/0 is a _______
(a) Positive rational number.
(b) Negative rational number.
(c) Either positive or negative rational number.
(d) Neither positive nor negative rational number.
Ans: (d)
Sol: Denominator is '0', it is not a rational number as it makes number undefined.
Q8. The number of rational numbers between two given rational numbers is
(a) Infinite
(b) Finite
(c) Two
(d) One
Ans: (a)
Sol: A rational number between two rational numbers a and b= (a + b) / 2
Like this, using this rational number (a + b) / 2 and b, we can find another rational number.
Hence, if we continue this, we get infinite rational numbers between two given rational numbers
Q9. The reciprocal of a positive rational number is positive.
(a) True
(b) False
(c) Cannot be determined
(d) None
Ans: (a)
Sol: The reciprocal of a positive rational number is positive.
Q10. How many rational numbers are there between −1 and 0?
(a) Infinite
(b) 1000
(c) 4990
(d) None
Ans: (a)
Sol: There are infinite number of rational numbers between any two integers.
Q11. -3/0 is a _______
(a) Negative rational number
(b) Positive rational number
(c) Either positive or negative rational number
(d) None of these
Ans: (d)
Sol: -3/0 is undefined. Which means that it is neither a negative rational number nor a positive rational number.
So option D is the correct answer.
Q12. -2/-19 is a ______
(a) Negative rational number
(b) positive rational number
(c) neither positive nor negative rational number
(d) None of these
Ans: (b)
Sol: Both the negative signs of the numerator and denominator will cancel each other out. So the given fraction is a positive rational number.
So option B is the correct answer.
Q13. While representing 2/3 on a number line, between which two integers does the point lie?
(a) 1 and 2
(b) 0 and 1
(c) 2 and 3
(d) 1 and 3
Ans: (b)
Sol: 2/3 = 0.67
It is clear that 0.67 lies between 0 and 1
So correct answer will be option (b)
Q14. For any two rational numbers x and y which of the following are correct, if x is positive and y is negative?
(1) x < y
(2) x = y
(3) x > y.
(a) Only 1 and 2 are correct
(b) Only 2 and 3 are correct
(c) Only 3 is correct
(d) All 1,2 and 3 are correct
Ans: (c)
Sol: If x is positive and y is negative, then the value of x will always be greater than value of y.
∴ x > y
Hence the correct answer is option (c)
Q15. State which of the following statements is/are true?
I. Numerator and denominator of a positive rational number need not to have like signs.
II. Numerator and denominator of a negative rational number should have like signs.
(a) Only I
(b) Only II
(c) Both I and II
(d) Neither I nor II
Ans: (d)
Sol: If both the numerator and denominator has same sign, then the fraction is a positive rational number.
If the numerator and denominator have different signs, then the fraction is a negative rational number.
Q16. Where does a rational number -2/3 lies on the number line?
(a) Lies to the left side of 0 on the number line
(b) Lies to the right side of 0 on the number line
(c) It is not possible to represent on the number line
(d) Cannot be determined on which side the number lies
Ans: (a)
Sol: -2/3 = -0.667
−0.667<0
Hence it will lie to the left side of 0 on the number line.
Q17. Express -125/625 as a rational number with smallest positive denominator equal to
(a) 25
(b) 5
(c) 625
(d) 125
Ans: (b)
Sol: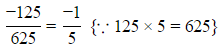
Q18. Express 126/-196 as a rational number with denominator equal to 14 then value of numerator will be
(a) 63
(b) −9
(c) −126
(d) None of these
Ans: (b)
Sol: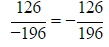
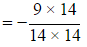
= -9/14
Q19. Between two rational numbers, there exists-
(a) No rational number
(b) Only one rational number
(c) Infinite numbers of rational numbers
(d) No irrational number
Ans: (c)
Sol: Between two rational numbers there are infinitely many rational number for example between 4 and 5 there are 4.1,4.2,.4.22,4.223.....
Hence, ((c)is the correct answer.
Q20. The product of two rational numbers is always:
(a)Rational
(b)Irrational
(c)Integer
(d)Whole number
Ans: (a)
Sol: The product of two rational numbers is always a rational number.
Q21. What is the additive inverse of 5/8?
(a)-8/5
(b)-5/8
(c)5/8
(d)8/5
Ans: (b)
Sol: The additive inverse of a number is the number that, when added to the original number, gives a sum of zero. The additive inverse of 5/8 is -5/8 because 5/8 + (-5/8) = 0.
Q22. Which of the following is a reciprocal of -3/4?
(a)-4/3
(b)3/4
(c)-3/4
(d)4/3
Ans: (a)
Sol: The reciprocal of a number 'a' is 1/a.
The reciprocal of -3/4 is -4/3.
Q23. Which of the following numbers is neither prime nor composite?
(a)1
(b)2
(c)9
(d)11
Ans: (a)
Sol: 1 is neither prime nor composite. A prime number has exactly two distinct positive divisors (1 and itself), while a composite number has more than two positive divisors. Since 1 has only one positive divisor (itself), it is neither prime nor composite.
Q23. Which of the following is a rational number between 5/8 and 3/4?
(a)11/16
(b)7/12
(c)4/7
(d)9/10
Ans: (a)
Sol: To find a rational number between two given rational numbers,
we take their average.
(5/8 + 3/4) / 2
= (5/8 + 6/8) / 2
= 11/16.
Thus, 11/16 is a rational number between 5/8 and 3/4.
Q24. Simplify: 5/6 + 2/3
(a)3/2
(b)7/9
(c)1 1/2
(d)11/18
Ans: (a)
Sol: 5/6 + 2/3
= 5/6 + 4/6
= (5 + 4)/6
= 9/6
= 3/2.
Q25. Which of the following is the multiplicative inverse of -5?
(a)-1/5
(b)5
(c)1/5
(d)-5
Ans: (c)
Sol: The multiplicative inverse (reciprocal) of a number 'a' is 1/a.
The multiplicative inverse of -5 is 1/(-5) = -1/5.
|
77 videos|386 docs|39 tests
|
















