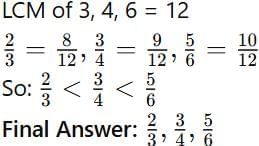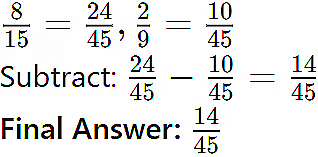Class 7 Exam > Class 7 Notes > Mathematics (Ganita Prakash) Class 7 - New NCERT > Practice Questions: Working with Fractions
Practice Questions: Working with Fractions | Mathematics (Ganita Prakash) Class 7 - New NCERT PDF Download
Q1. Mark has 3/4 kg of flour and uses 1/8 kg for each cookie batch. How many batches can he make?
Sol:
Total flour = 3/4 kg
Flour per batch = 1/8 kg
Number of batches = Total flour ÷ Flour per batch
= (3/4) ÷ (1/8)
= (3/4) × (8/1)
= (3 × 8) / 4
= 24 / 4
= 6
Q2. A string of 4/7 meter is cut into 8 equal pieces. What is the length of each piece?
Sol:
Total length = 4/7 meter
Number of pieces = 8
Length per piece = Total length ÷ Number of pieces
= (4/7) ÷ 8
= (4/7) × (1/8)
= 4 / 56
= 1 / 14 meter
Q3. Simplify: (3/4) × (8/9) ÷ (2/3)
Sol:
Perform multiplication and division from left to right:
(3/4) × (8/9)
= (3 × 8) / (4 × 9)
= 24 / 36
= 2 / 3
(2/3) ÷ (2/3)
= (2/3) × (3/2)
= (2 × 3) / (3 × 2)
= 6 / 6
= 1
Q4. Each side of a square tile is 3/4 meter. Find its area.
Sol:
Area of a square = side × side
Side = 3/4 meter
Area = (3/4) × (3/4) = 9 / 16 m2
Q5. A printer can print 2/3 pages in one minute. How many minutes will it take to print 8/5 pages?
Sol:
Pages per minute = 2/3
Total pages to print = 8/5
Time required = Total pages ÷ Pages per minute
= (8/5) ÷ (2/3)
= (8/5) × (3/2)
= (8 × 3) / (5 × 2) = 24 / 10 = 12 / 5 minutes.
Q6. Divide the sum of 5/6 and 2/3 by 3/4.
Sol:
Sum of fractions:
5/6 + 2/3 = 5/6 + 4/6 = 9/6 = 3/2
Divide by 3/4:
(3/2) ÷ (3/4) = (3/2) × (4/3)
= (3 × 4) / (2 × 3)
= 12 / 6
= 2
Q7.Arrange in ascending order: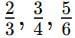 
Sol:
Q8. Simplify and reduce to lowest terms: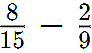 
Sol: LCM of 15 and 9 = 45
The document Practice Questions: Working with Fractions | Mathematics (Ganita Prakash) Class 7 - New NCERT is a part of the Class 7 Course Mathematics (Ganita Prakash) Class 7 - New NCERT.
All you need of Class 7 at this link: Class 7
|
41 videos|251 docs|8 tests
|
FAQs on Practice Questions: Working with Fractions - Mathematics (Ganita Prakash) Class 7 - New NCERT
| 1. What are the basic operations that can be performed with fractions? |  |
Ans. The basic operations that can be performed with fractions include addition, subtraction, multiplication, and division. To add or subtract fractions, they must have a common denominator. For multiplication, you multiply the numerators together and the denominators together. For division, you multiply by the reciprocal of the second fraction.
| 2. How do you simplify a fraction? | |
Ans. To simplify a fraction, you need to divide both the numerator and the denominator by their greatest common divisor (GCD). For example, to simplify 8/12, the GCD of 8 and 12 is 4. Dividing both by 4 gives you 2/3, which is the simplified form.
| 3. What is the difference between a proper fraction and an improper fraction? | |
Ans. A proper fraction is a fraction where the numerator is less than the denominator, such as 3/4. An improper fraction, on the other hand, has a numerator that is greater than or equal to the denominator, such as 5/4 or 6/6. Improper fractions can also be converted into mixed numbers.
| 4. How can you convert a mixed number into an improper fraction? | |
Ans. To convert a mixed number into an improper fraction, multiply the whole number by the denominator of the fractional part, then add the numerator of the fractional part. This sum becomes the new numerator while retaining the same denominator. For example, to convert 2 1/3 into an improper fraction: (2 × 3) + 1 = 7, so it becomes 7/3.
| 5. Why is it important to find a common denominator when adding or subtracting fractions? | |
Ans. Finding a common denominator is important when adding or subtracting fractions because it allows you to combine the fractions accurately. Without a common denominator, the fractions represent different parts of a whole and cannot be directly added or subtracted. The common denominator ensures that both fractions are expressed in terms of the same size parts.
About this Document
4.91/5
Rating
Sep 26, 2025
Last updated
Related Exams
Document Description: Practice Questions: Working with Fractions for Class 7 2025 is part of Mathematics (Ganita Prakash) Class 7 - New NCERT preparation.
The notes and questions for Practice Questions: Working with Fractions have been prepared according to the Class 7 exam syllabus. Information about Practice Questions: Working with Fractions covers topics
like and Practice Questions: Working with Fractions Example, for Class 7 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Practice Questions: Working with Fractions.
Introduction of Practice Questions: Working with Fractions in English is available as part of our Mathematics (Ganita Prakash) Class 7 - New NCERT
for Class 7 & Practice Questions: Working with Fractions in Hindi for Mathematics (Ganita Prakash) Class 7 - New NCERT course.
Download more important topics related with notes, lectures and mock test series for Class 7
Exam by signing up for free. Class 7: Practice Questions: Working with Fractions | Mathematics (Ganita Prakash) Class 7 - New NCERT
Description
Full syllabus notes, lecture & questions for Practice Questions: Working with Fractions | Mathematics (Ganita Prakash) Class 7 - New NCERT - Class 7 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Ganita Prakash) Class 7 - New NCERT | Best notes, free PDF download
Information about Practice Questions: Working with Fractions
In this doc you can find the meaning of Practice Questions: Working with Fractions defined & explained in the simplest way possible. Besides explaining types of
Practice Questions: Working with Fractions theory, EduRev gives you an ample number of questions to practice Practice Questions: Working with Fractions tests, examples and also practice Class 7
tests
Related Searches
past year papers
,practice quizzes
,Practice Questions: Working with Fractions | Mathematics (Ganita Prakash) Class 7 - New NCERT
,Semester Notes
,Practice Questions: Working with Fractions | Mathematics (Ganita Prakash) Class 7 - New NCERT
,Summary
,Objective type Questions
,Exam
,ppt
,mock tests for examination
,Practice Questions: Working with Fractions | Mathematics (Ganita Prakash) Class 7 - New NCERT
,shortcuts and tricks
,Free
,Viva Questions
,MCQs
,study material
,video lectures
,Extra Questions
,Sample Paper
,Previous Year Questions with Solutions
,Important questions
;
Additional Information about Practice Questions: Working with Fractions for Class 7 Preparation
Practice Questions: Working with Fractions Free PDF Download
The Practice Questions: Working with Fractions is an invaluable resource that delves deep into the core of the Class 7 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Practice Questions: Working with Fractions now and kickstart your journey towards success in the Class 7 exam.
Importance of Practice Questions: Working with Fractions
The importance of Practice Questions: Working with Fractions cannot be overstated, especially for Class 7 aspirants.
This document holds the key to success in the Class 7 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Practice Questions: Working with Fractions Notes
Practice Questions: Working with Fractions Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Practice Questions: Working with Fractions.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Practice Questions: Working with Fractions Notes on EduRev are your ultimate resource for success.
Practice Questions: Working with Fractions Class 7
The "Practice Questions: Working with Fractions Class 7 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 7 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Practice Questions: Working with Fractions on the App
Students of Class 7 can study Practice Questions: Working with Fractions alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Practice Questions: Working with Fractions,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Practice Questions: Working with Fractions is prepared as per the latest Class 7 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily