Prestressed Concrete - 2 | Additional Documents & Tests for Civil Engineering (CE) PDF Download
Basic Assumptions
1. Concrete is a homogeneous elastic material.
2. Within the range of working stress, both concrete & steel behave elastically, notwithstanding the small amount of creep, which occurs in both the materials under sustained loading.
3. A plane section before bending is assumed to remain plane even after bending, which implies a linear strain distribution across the depth of the member.
- Prestress Concrete is one in which there have been introduced internal stresses of such magnitude and distribution that stresses resulting from given external loading is counterbalanced to a desired degree.
Analysis of prestress and Bending stress
Following are the three concepts of analysis
- Stress concept analysis
- Strength concept analysis
- Load balancing method
- Stress concept Method
Following are the two cases for analysis
Case-(i): Beam provided with a concentric tendon: Let, P prestressing force applied by the tendon. Due to this prestressing force, the direct compressive force induced is given by, fa = P/A.
Let, P prestressing force applied by the tendon. Due to this prestressing force, the direct compressive force induced is given by, fa = P/A.
If due to dead load & external loads, the bending moment at the section is M, then the extreme stresses at the section due to bending moment alone is f0 = ±M/Z
Hence final stress at the extreme top edge = P/A + M/Z and stress at the extreme bottom edge = P/A - M/Z
Case–(ii): Beams with eccentrics tendon: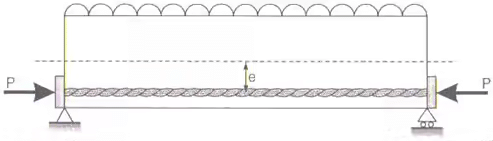
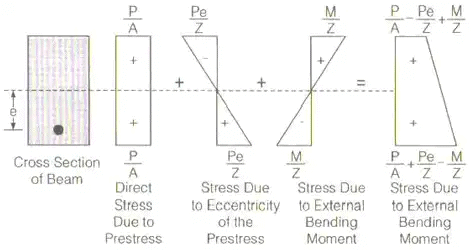 (i) Direct stresses due to prestressing force = +P / A
(i) Direct stresses due to prestressing force = +P / A
(ii) Extreme stresses due to an eccentricity of the prestressing force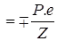
(iii) Extreme stresses due to bending moment = ±M/Z
Final stresses
Stress at top fibre = P / A - P.e / Z + M / Z
Stress at bottom fibre = P / A + P.e / Z - M / Z
By providing an eccentricity to the tendon, a hogging moment (P.e.) is developed which will produce stresses, which will counteract the stresses due to external bending moment. - Strength Concept method
Consider a beam of length l provided with a tendon at an eccentricity e. Suppose the beam is lying on the ground i.e. the beam is not subjected to any external load. Hence there is no external bending moment on the beam.
 The following equal forces are existing
The following equal forces are existing
(i) The P-force which is the tension in the tendon.
(ii) The C-force which is the compressive force acting on the concrete.
Stresses in concrete are produced entirely due to C-force.
In the absence of any external bending moment the C-force and P-force act at the same level. Line of action of P-force is called the P-line. The P-line is nothing but the tendon line itself. The line of action of the C-force is called the C-line or Pressure line. Hence in the absence of any external bending moment, the P-line and the C-line coincide.
Suppose the beam is subjected to a bending moment M, then the C-line will be shifted from the P-line by a distance 'a' called lever arm.
α = M / P = M / C
Extreme stresses in concrete are given by
- Load Balancing Concept
Prestressed Beam with Bent Tendon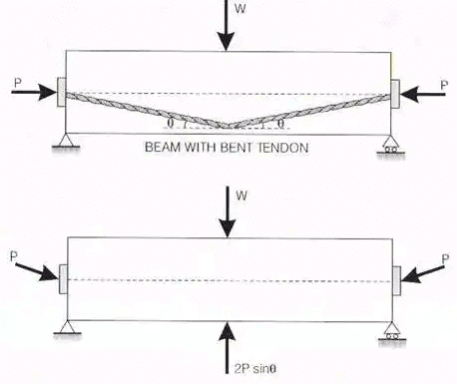 By providing bent tendons, the tendons will exert upward pressure on the concrete beam and will therefore counteract a part of the external downward loading.
By providing bent tendons, the tendons will exert upward pressure on the concrete beam and will therefore counteract a part of the external downward loading.
Considering the concrete as a free body. We find an upward force 2P sin θ.
The net downward load at the centre will be (W-2P sinθ)
The axial longitudinal force provided by the tendon = Pcosθ = P {since θ is small}
Direct stress on the section = Pcosθ / A = P / A
Net BM,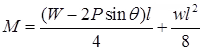
Where, w = dead load per unit length of the beam. Extreme fibre stress = P / A ± M / Z
It may be realized that the profile of the tendon should follow the shape of the bending moment diagram for the given external loads in the order it may offer considerable and effective upward forces. For e.g., if the loading on the beam is a uniformly distributed load, the tendon may be provided along with a parabolic profile.
Tendon with Parabolic Profile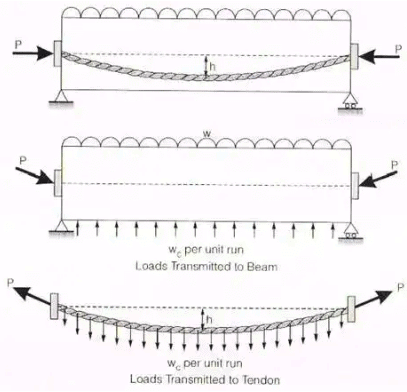 Let l be the span of the beam and h be the dip of the cable.
Let l be the span of the beam and h be the dip of the cable.
The cable will exert an upward udl = wC / m on the beam, but the cable will be subjected to a downward udl of wC per unit run.
Let V and H are vertical and horizontal components of P.
V = wcl / 2
The cable is an absolutely flexible member, therefore BM at every section of cable is zero. Hence BM at the centre of the cable is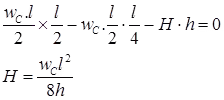
Since dip of the cable is very small, we can make an approximation
cosα = 1 and Pcosα = P
Now consider the beam, it is subjected to
(i) External load w per unit length
(ii) Upward udl transmitted by the cable = wC per unit length.
Net UDL = w – wC
Net BM at the centre 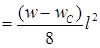
Extreme stresses = P / A ± Net BM / Z
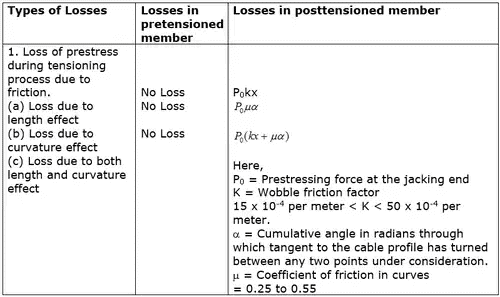
Losses of Prestress
The steel wires of a prestressed concrete member do not retain all the preliminary prestress. A certain amount of loss of prestress always takes place.
Losses may be classified as follows:



FAQs on Prestressed Concrete - 2 - Additional Documents & Tests for Civil Engineering (CE)
| 1. What is prestressed concrete? |  |
| 2. How does prestressed concrete differ from conventional reinforced concrete? |  |
| 3. What are the advantages of using prestressed concrete? |  |
| 4. What are the common applications of prestressed concrete? |  |
| 5. What are the challenges associated with prestressed concrete construction? |  |





















