Class 10 Maths Chapter 5 Previous Year Questions - Arithmetic Progressions
| Table of contents |

|
| Previous Year Questions 2024 |

|
| Previous Year Questions 2023 |

|
| Previous Year Questions 2022 |

|
| Previous Year Questions 2020 |

|
| Previous Year Questions 2019 |

|
| Previous Year Questions 2017 |

|
Previous Year Questions 2024
Q1: The ratio of the 10th term to its 30th term of an A.P. is 1 : 3 and the sum of its first six terms is 42. Find the first term and the common difference of A.P. (CBSE 2024)
 View Answer
View Answer 
Ans:
Let the AP be a, a + d, a + 2d,.............
T10T30 = 13
⇒ a + 9da + 29d = 13
⇒ 3a + 27d = a + 29d
⇒ 3a - a = 29d - 27d
⇒ 2a - 2d = 0
⇒ 2a = 2d
∴ a = d …(i)
Now, S6 = 42
62 [2a + (6 - 1)d] = 42
⇒ 3[2a + 5d] = 42
⇒ 2a + 5d =14
⇒ 2a + 5a = 14 [From eqn (i)]
⇒ 7a = 14
⇒ a = 14/7
∴ a = 2
So First term = 2
Common difference = 2.
Q2: If the sum of the first 7 terms of an A.P. is 49 and that of the first 17 terms is 289, find the sum of its first 20 terms. (CBSE 2024)
 View Answer
View Answer 
Ans:
S7 = 49
72 [2a + (7-1)d] = 49
⇒ 2a + 6d = 14
⇒ a + 3d = 7 …(i)
S17 = 289
172 [2a + 16d] = 289
⇒ 2a + 16d = 289 × 217
⇒ 2(a + 8d) = 34
⇒(a + 8d) = 34 / 2
⇒ a + 8d = 17 …(ii)
From eqn (i) and (ii):
⇒ -5d = -10
∴ d = 2
Put the value of d in eqn (i):
⇒ a + 3 × 2 = 7
⇒ a + 6 = 7
⇒ a = 7 - 6
⇒ a = 1
∴ S20 = 202 [2(1) + (20 - 1)2]
⇒ 10 [2 + 19 × 2]
⇒ 10 [2 + 38]
⇒ 40 × 10
⇒ 400
Previous Year Questions 2023
Q1: If a, b, form an A.P. with common difference d. then the value of a - 2b - c is equal to (2023)
(a) 2a + 4d
(b) 0
(c) -2a- 4d
(d) -2a - 3d
 View Answer
View Answer 
Ans: (c)
Sol: We have, a, b, c are in A.P.
b = a + d, and c = a + 2d
Now, a - 2b - c = a - 2(a + d) - (a + 2d)
= a - 2a - 2d - a - 2d
= -2a- 4d
Q2: If k + 2, 4k - 6. and 3k - 2 are three consecutive terms of an A.P. then the value of k is (2023)
(a) 3
(b) -3
(c) 4
(d) -4
 View Answer
View Answer 
Ans: (a)
Sol: Since, k + 2, 4k - 6 and 3k - 2 are three consecutive terms of A.P.
a2 - a1 = a3 - a2
⇒ (4k - 6)- (k + 2) = (3k - 2) - (4k - 6)
⇒ 4k -6 - k - 2= 3k - 2 - 4k + 6
⇒ 3k - 8 = -k + 4
⇒ 4k = 12
⇒ k = 3
Q3: How many terms are there in A.P. whose first and fifth terms are -14 and 2, respectively and the last term is 62. (CBSE 2023)
 View Answer
View Answer 
Ans: We have
First term, a1 = - 14
Fifth term, a5 = 2
Last term, an = 62
Let d be the common difference and n be the number of terms.
∵ a5 = 2
⇒ -14 +(5 - 1)d = 2
⇒ 4d = 16
⇒ d =4
Now, an = 62
⇒ -14 + (n - 1)4 = 62
⇒ 4n - 4 = 76
⇒ 4n = 80
⇒ n= 20
There are 20 terms in A.P.
Q4: Which term of the A.P. : 65, 61, 57, 53, _____ is the first negative term? (CBSE 2023)
 View Answer
View Answer 
Ans: Given, A.P. is 65, 61, 57, 53,.....
Here, first term a = 65 and common difference, d = -4
Let the nth term is negative.
Last term, an = a + (n - 1) = 65 + (n - 1)(-4)
= 65 - 4n + 4
= 69 - 4n, which will be negative when n = 18
So, 18th term is the first negative term.
Q5: Assertion: a, b, c are in AP if and only if 2b = a + c
Reason: The sum of the first n odd natural numbers is n2. (CBSE 2023)
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
 View Answer
View Answer 
Ans: (b)
Sol: Since, a, b ,c are in A.P. then b - a = c -b
⇒ 2b = a + c
First n odd natural number be 1, 3, 5 ..... (2n - 1).
which form an A.P. with a = 1 and d = 2
Sum of first n odd natural number = n/2[2a + (n -1)d]
= n/2 [2 + (n - 1)2] = n2
Hence, assertion and reason are true but reason is not the correct explanation of assertion.
Q6: The sum of the first 15 terms of an A.P. is 750 and its first term is 15. Find its 20th term. (2023)
 View Answer
View Answer 
Ans: Here, a = 15 and S15 = 750
∵ Sn = n/2[2a + (n -1)d]
∴ S15 = 15/2 [2 x 15 + (15 -1)d] = 750
⇒ 15(15 + 7d) = 750
⇒ 15 + 7d = 50
⇒ 7d = 35
⇒ d = 5
Now, 20th term = a + (n - 1)d
= 15 + (20 - 1) 5
= 15 + 95
= 110
Q7: Rohan repays his total loan of Rs. 1,18,000 by paying every month starting with the first installment of Rs. 1,000. If he increases the installment by Rs. 100 every month. what amount will be paid by him in the 30th installment? What amount of loan has he paid after the 30th installment? (2023)
 View Answer
View Answer 
Ans: Total amount of loan Rohan takes = Rs. 1,18,000
First installment paid by Rohan = Rs. 1000
Second instalment paid by Rohan = 1000 + 100 = Rs. 1100
Third installment paid by Rohan = 1100 + 100 = Rs. 1200 and so on.
Let its 30th installment be n.
Thus, we have 1000,1100,1200, which forms an A.P. with first term (a) = 1000
and common difference (d) = 1100 - 1000 = 100
nth term of an A.P. an= a + (n - 1)d
For 30th installment, a30 = a + (30 - 1)d
= 1000 + (29) 100 = 1000 + 2900 = 3900
So Rs. 3900 will be paid by Rohan in the 30th installment.
Now, we have a = 1000, last term (l)= 3900
Sum of 30 installment, S30 = 30/2[a + 1]
⇒ S30 = 15(1000 + 3900) = Rs. 73500
Total amount he still have to pay after the 30th installment = (Amount of loan) - (Sum of 30 installments)
= Rs. 1,18,000 - Rs. 73,500 = Rs. 44,500
Hence, Rs. 44,500 still has to be paid after the 30th installment.
Q8: The ratio of the 11th term to the 18th term of an AP is 2:3. Find the ratio of the 5th term to the 21st term and also the ratio of the sum of the first five terms to the sum of the first 21 terms. (2023)
 View Answer
View Answer 
Ans: Let a and d be the first term and common difference of an AP.
Given that, a11 : a18 = 2 : 3
⇒ a + 10da + 17d = 23
⇒ 3a + 30d = 2a + 34d
⇒ a = 4d ...(i)
Now, a5 = a + 4d = 4d + 4d = 8d [from Eq.(i)]
And a21 = a + 20d = 4d + 20d = 24d [from Eq. (i)]
a5 : a21 = 8d : 24d = 1 : 3
Now, sum of the first five terms, S5 = 5/2 [2a + (5−1)d]
= 5/2 [2(4d) + 4d] [from Eq.(i)]
= 5/2 (8d + 4d) = 5/2 × 12d = 30d
And, sum of the first 21 terms, S21 = 21/2 [2a + (21−1)d]
= 21/2 [2(4d) + 20d]= 21/2 × 28 d = 294 d from Eq..(i)]
So, ratio of the sum of the first five terms to the sum of the first 21 terms is,
S5 : S21 = 30d : 294d = 5 : 49
Q9: 250 logs are stacked in the following manner: 22 logs in the bottom row, 21 in the next row, 20 in the row next to it and so on (as shown by an example). In how many rows, are the 250 logs placed and how many logs are there in the top row?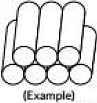
 View Answer
View Answer 
Ans: Let there be n rows to pile of 250 logs
Here, the bottom row has 22 logs and in next row, 1 log reduces
It means, we get an AP 22, 21, 20, 19, ..................... n with first term or a = 22 and d = -1
Now, we know that total logs are 250 or we can say that,
Sn =250
Since sum of n terms of an A.P. Sn = n/2 (2a + (n-1) d)
= 250 Therefore, n/2 (2 x 22 + (n-1) x (-1))
or 500 = n (44 - (n-1))
500 = n (45- n)
n2 - 45 n + 500 = 0
n2 - 25n - 20n + 500 = 0
n(n - 25) - 20(n - 25) = 0
By solving this, we get (n-20) (n-25) = 0
Since, there are 22 logs in first row and in next row, 1 log reduces, then we can not have more than 22 terms
∴ n ≠ 25
and n = 20
Means, 20th row is the top row of the pile
Now let's find out number of logs in 20th row
We know that value of nth term of an A.P. = a + (n-1) d
n20 = [22 + (20-1) (-1)]
=(22-19) = 3
Therefore, there are 3 logs in the top row.
Q10: The next term of the A.P.: √7, √28, √63 is:
(a) √70
(b) √80
(c) √97
(d) √112 (CBSE 2023)
 View Answer
View Answer 
Ans: (d)
Given an AP √7, √28, √63, ....
Examine the given conditions.
Therefore,
Hence, the next term i.e., 4th term will be,
⇒ aₙ = a + (n - 1)d
⇒ a₄ = √7 + (4 - 1)√7
⇒ a₄ = √7 + 3√7
Therefore, the next term of an AP
√7, √28, √63, .. is √112.
Hence, the correct option is 4.
Previous Year Questions 2022
Q1: Find a and b so that the numbers a, 7, b, 23 are in A.P. (2022) View Answer
View Answer 
Ans: Since a, 7, b, 23 are in A.P.
∴ Common difference is same.
∴ 7 - a = b -7 = 23 - b
Taking second and third terms, we get
b - 7 = 23 - b
⇒ 2b = 30
⇒ b = 15
Taking first and second terms, we get
⇒ 7 - a = b - 7
⇒ 7 - a = 15 - 7
⇒ 7 - a = 8
⇒ a = -1
Hence, a = -1, b = 15.
Q2: Find the number of terms of the A.P. : 293, 235, 177,....., 53 (2022)
 View Answer
View Answer 
Ans:
First term (a) = 293
Common difference (d) = 235 − 293 = -58
Last term (aₙ) = 53
Formula:
aₙ = a + (n - 1)d
Substitute values:
53 = 293 + (n - 1)(-58)
53 = 293 - 58(n - 1)
53 - 293 = -58(n - 1)
-240 = -58(n - 1)
Solve for (n - 1):
n - 1 = (-240) / (-58)
n - 1 = 240 / 58
n - 1 = 120 / 29
Add 1:
n = 1 + 120/29
n = (29 + 120) / 29
n = 149/29
Since n is not an integer, this means 53 is not a term of this A.P. and the question has no natural number solution for n.
Q3: Determine the A.P. whose third term is 5 and the seventh term is 9. (2022)
 View Answer
View Answer 
Ans: Let the first term and common difference of an A.P. be a and d, respectively.
Given a3= 5 and a7 = 9
a + (3 - 1 ) d = 5 and a + (7 - 1)d = 9
a + 2d = 5 --------------(i)
and a + 6d = 9--------------(ii)
On subtracting (i) from (ii), we get
⇒ 4d = 4
⇒ d = 1
From (i), a + 2(1) = 5 ⇒ a + 2 = 5 ⇒ a = 3
So. required A.P. is a, a + d, a + 2d, a + 3d......
i.e. 3, 3 +1, 3 + 2(1), 3 + 3(1), ....., i.e.. 3, 4, 5, 6, .....
Previous Year Questions 2020
Q1: If -5/7, a, 2 are consecutive terms in an Arithmetic Progression, then the value of a' is (2020)(a) 9/7
(b) 9/14
(c) 19/7
(d) 19/14
 View Answer
View Answer 
Ans: (b)
Sol: Given, -5/7, a, 2 are in A.P. therefore common difference is same.
∴ a2 - a1 = a3 - a2
a - -57 = 2 - a
⇒ a + 57 = 2 - a
⇒ 2a = 97
⇒ a = 914
Q2: Which of the following is not an A.P? (2020)
(a) -1.2, 0.8.2.8, ....
(b) 3, 3+√2, 3+2√2,3 + 3√2,...
(c) 4/3, 7/3, 9/3, 12/3, ...
(d) -1/5, -2/5, -3/5,..
 View Answer
View Answer 
Ans: (c)
Sol: In option (c), We have
a2 - a1 = 73 = 43 = 33 = 1
a3 - a2 = 93 = 73 = 23
As a2 - a1 ≠ a3- a2 the given list of numbers does not form an A.P.
Q3: The value of x for which 2x, (x + 10) and (3x + 2) are the three consecutive terms of an A.P, is (2020)
(a) 6
(b) -6
(c) 18
(d) -18
 View Answer
View Answer 
Ans: (a)
Sol: Given, 2x, (x + 10) and (3x + 2) are in A.P.
(x + 10) - 2x = (3x + 2) - (x + 10)
⇒ -x + 10= 2x - 8
⇒ - 3x = -18
⇒ x = 6
Q4: Show that (a - b)2, (a2 + b2) and (a + b)2 are in A.P. (2020)
 View Answer
View Answer 
Ans: Let a1 = (a - b)2, a2 = (a2 + b2) and a3= (a + b)2
Now. a2 - a1 = (a2 + b2) - (a - b)2
= a2 + b2 - (a2 + b2 - 2ab)
= a2 + b2- a2- b2 + 2ab = 2ab
Again a3 - a2 = (a + b)2 - (a2 + b2)
= a2 + b2 + 2ab - a2 - b2 = 2ab
∴ a2 - a1 = a3 - a2
So, (a - b)2, (a2 + b2) and (a + b)2 are in A.P.
Q5: The sum of four consecutive numbers in A.P. is 32 and the ratio of the product of the first and last terms to the product of two middle terms is 7 : 15. Find the numbers. (2020)
 View Answer
View Answer 
Ans: Let the four consecutive numbers be (a - 3d), (a - d), (a + d), (a + 3d).
Sum of four numbers = 32 (Given)
⇒ (a - 3d) + (a - d) + (a + d) + (a + 3d) = 32
⇒ 4a = 32 ⇒ a = 8
Also, (a - 3d)(a + 3d)(a - d)(a + d) = 715
⇒ a2 - 9d2a2 - d2 = 715
⇒ 15a2 - 135d2 = 7a2 - 7d2
⇒ 8a2 = 128d2
⇒ d2 = 8a2128 = 8 × 64128
⇒ d = ± 2
If d = 2. then the numbers are (8 - 6), (8 - 2), (8 + 2) and (8 + 6) i.e., 2,6, 10, 14 .
If d = -2. then the numbers are (8 + 6), (8 + 2), (8 - 2). (8 - 6) i.e.,14 ,10 ,6 ,2 .
Hence, the numbers are 2, 6, 10, 14 or 14, 10, 6, 2.
Q6: Find the sum of the first 100 natural numbers. (CBSE 2020)
 View Answer
View Answer 
Ans: First 100 natural numbers are 1 , 2 , 3 ...... 100 which form an A.P. with a = 1, d = 1.
Sum of n terms =Sn = n/2 [2a + (n - 1)d]
= 100/2 [2 x 1 + (100 - 1) x 1]
= 50 [2 + 99] = 50 x 101 = 5050
Q7: Find the sum of the first 16 terms of an Arithmetic Progression whose 4th and 9th terms are - 15 and - 30 respectively. (2020)
 View Answer
View Answer 
Ans: Given, a4 = -15 and a9 = -30
a + 3d = - 15 (i)
a + 8d = -30 (ii)
On subtracting (ii)from (i), we have
-5d = 15
⇒ d = - 3
Put d = - 3 in (i), we have
a + 3(-3)= - 15
⇒ a - 9 = - 15
⇒ a = - 6
Now, Sn = n/2 [2a + (n - 1)d]
⇒ S16 = 16/2 [2(-6) + (16 - 1) (-3)]
= 8 [2(-6) + (15) (-3)] = 8 [-12 - 45] = -456
Q8: In an A.P. given that the first term (a) = 54. the common difference (d) = -3 and the nth term (an) = 0. Find n and the sum of the first n terms (Sn) of the A.P. (2020)
 View Answer
View Answer 
Ans: Given, d = - 3, a = 54 and an= 0
Since an = a + (n -1)d
∴ 0 = 54 + (n - 1)(-3)
⇒ 0 = 54 - 3n + 3
⇒ 3n = 57
⇒ n = 19
Now,
Sn = n/2 [2a+(n-1)d]
= 19/2 [2 × 54 +(19 - 1)(-3)]
= 19/2 [108 - 54] = 19/2 × 54 = 513
Q9: Find the Sum (−5) + (−8)+ (−11) + ... + (−230). (2020)
 View Answer
View Answer 
Ans: (−5) + (−8) + (−11) + ... + (−230) .
Common difference of the A.P. (d) = a2 - a1
= -8-(-5)
= -8+5
= -3
So here,
First term (a) = −5
Last term (l) = −230
Common difference (d) = −3
So, here the first step is to find the total number of terms. Let us take the number of terms as n.
Now, as we know,
an = a + (n-1) d
So, for the last term,
- 230 = -5 + ( n-1) (-3)
- 230 = -5 - 3n + 3
-230 + 2 = -3n
- 228/-3 = n
n = 76
Now, using the formula for the sum of n terms, we get
Sn = 76/2 [2(-5) + (76-1)(-3)]
= 38 [-10 + (75)(-3)]
=38 (-10-225)
= 38(-235)
= -8930
Therefore, the sum of the A.P is Sn = -8930
Q10: Show that the sum of all terms of an A.P. whose first term is a, the second term is b and the last term is c is equal to (a + c)(b + c - 2a)2(b - a) . (CBSE 2020)
 View Answer
View Answer 
Ans: Given: first term a1 = a, second term, a2 = b and last term, l = c.
So, common difference, d = a2 – a1 = b – a
Let this A.P. contains n terms.
Then, l = a + (n – 1)d
⇒ c = a + (n – 1) (b – a)
⇒ c – a = (n – 1)(b – a)
⇒ n - 1 = c - ab - a
⇒ n = c - ab - a + 1
⇒ n = c - a + b - ab - a
⇒ n = b + c - 2ab - a …(i)
Now, sum of n terms of A.P. is given by:
Sn = n2 [a + l]
⇒ Sn = 12 [b + c - 2ab - a] [a + c] [Using (i)]
⇒ Sn = (a + c)(b + c - 2a)2(b - a)
Hence, proved.
Previous Year Questions 2019
Q1: Write the common difference of A.P. (2019)√3, √12, √27, √48, ......
 View Answer
View Answer 
Ans: Give A.P. is
√3, √12, √27, √48, ......
or √3, 2√3, 3√3,4√3, .......
∴ d = common difference = 2√3 - √3 = √3
Q2: Which term of the A.P. 10, 7, 4, ...is -41? (2019)
 View Answer
View Answer 
Ans: Let nth term of A.P. 10, 7, 4, ...is -41
∴ an = a + (n - 1)d
⇒ - 41 = 10+(n-1)(-3) [∵ d = 7 - 10 = -3]
⇒ - 41 = 10 - 3n + 3
⇒ -41 = 13 - 3n
⇒ 3n = 54
⇒ n= 18
∴ 18th term of given A.P. is - 41
Q3: If in an A.P. a = 15, d = - 3 and an = 0, then find the value of n. (2019)
 View Answer
View Answer 
Ans: Given, a = 15, d = - 3 and an = 0
∴ an = a + (n - 1)d
⇒ 15 + (n - 1 )(- 3)= 0
⇒ 15 - 3n +3 = 0
⇒ 18 - 3n = 0
⇒ - 3n = -18
⇒ n = 6
Q4: How many two-digit numbers are divisible by 3? (2019)
 View Answer
View Answer 
Ans: Two-digit numbers which are divisible by 3 are 12, 15, 13..... 99. which forms an A.P. with first term (a) = 12, common difference (d) = 15 - 12 = 3 and last term (l) or nth term = 99
a + (n - 1)d = 99
⇒ 12 + (n - 1)3 = 99
⇒ 3n = 99 - 9
⇒ n = 90/3
⇒ n = 30
Q5: If the 9th term of an AR is zero, then show that its 29th term is double its 19th term. (2019, 2 Marks)
 View Answer
View Answer 
Ans: Given, a9 = 0 . we have to show that a29 = 2a19
a + 8d = 0
⇒ a = - 8 d
Now, a19 = a + 18d = -8d + 18d = 10d
a29 = a + 28d = -8d + 28d = 20d = 2(10d ) = 2a19
Hence, a29 = 2a19
Q6: Which term of the A.P. 3, 15, 27, 39, ... will be 120 more than its 21st term? (CBSE 2019)
 View Answer
View Answer 
Ans: We have, first term, a = 3, common difference, d = 15 - 3 =12
nth term of an A.P. is given by an = a + (n - 1)d
∴ a21 = 3 + (20) x 12
= 3 + 240
= 243
Let the rth term of the AP. be 120 more than the 21st term.
⇒ a + (r - 1) d = 243 + 120
⇒ 3 + (r - 1) 12 = 363
⇒ (r - 1) 12 = 360
⇒ r - 1= 30
⇒ r = 31
Q7: If the 17th term of an A.P. exceeds its 10th term by 7, find the common difference. (2019)
 View Answer
View Answer 
Ans: According to question, a17 - a10 = 7
i.e. a + 16d- (a + 9d) = 7
where a = first term d = common difference
⇒ 7d = 7
∴ d = 1
Q8: Ramkali would require ₹ 5000 to get her daughter admitted to a school after a year. She saved ₹ 150 in the first month and increased her monthly savings by ₹ 50 every month. Find out if she will be able to arrange the required money after 12 months. Which value is reflected in her efforts? (CBSE 2019, 15)
 View Answer
View Answer 
Ans: The saving in first month is₹ 150.
The saving in second month is
₹(150 + 50) = ₹ 200
Similarly, saving goes on increasing every month by ₹ 50.
Savings = ₹ 150, ₹ 200, ₹ 250, ₹300,.....
Savings forms an A.P. in which first term (a) = 150 and common difference, (d) = 50
Then, total savings for 12 months
S12 = n2 [2a + (n - 1)d]
⇒ S12 = 122 [2 × 150 + (12 - 1) × 50]
⇒ S12 = 6 [300 + 550]
⇒ S12 = 6 × 850 = ₹ 5100
Then, Ramkali would be able to save ₹ 5,100 in 12 months and she needs ₹5,000 to send her daughter to school.
Hence, Ramkali would be able to send her daughter to school.
Values: Putting efforts to send her daughter to school shows her awareness regarding girls education and educating a child.
Previous Year Questions 2017
Q1: A sum of ₹ 4,250 is to be used to give 10 cash prizes to students of a school for their overall academic performance. If each prize is ₹ 50 less than its preceding prize, find the value of each of the prizes. (CBSE 2017) View Answer
View Answer 
Ans: Let the value of first most expensive prize be ₹ a.
Then, according to the given condition, prizes are a, a – 50, a – 100, a – 150 .......
The given series forms an A.P., with a common difference of (– 50).
Here, first term = a
Common difference d = – 50
Number of terms, n = 10 and,
sum of 10 terms, S10 = ₹ 4,250
By formula, Sn = n2 [2a + (n - 1)d]
⇒ S10 = 102 [2 × a + (10 - 1) × (-50)]
⇒ 4250 = 5(2a - 450)
⇒ 850 = 2a - 450
⇒ a = 13002 = ₹ 650
Hence, the value of the prizes are: ₹ 650, ₹ 600, ₹ 550, ₹ 500, ₹ 450, ₹ 400, ₹ 350, ₹ 300, ₹ 250, ₹ 200.
Q2: A child puts one five-rupee coin of her savings in the piggy bank on the first day. She increases her savings by one five-rupee coin daily. If the piggy bank can hold 190 coins of five rupees in all, find the number of days she can continue to put the five-rupee coins into it and find the total money she saved. Write your views on the habit of saving. (CBSE 2017)
 View Answer
View Answer 
Ans: Since, child puts ₹ 5 on 1st day, ₹ 10 (2 × 5) on
2nd day, ₹ 15(3 × 5) on 3rd day and so on.
Total savings = 190 coins = 190 × 5 = ₹ 950
So, the series of her daily savings is, ₹ 5, ₹ 10, ₹ 15, .....
Clearly, this series is an A.P.
So, first term, a = 5
Common difference, d = 5
Sum of total savings, Sn = 950
Let, n be the last day when piggy bank becomes full.
∴ Sn = n2 [2a + (n - 1)d]
⇒ 950 = n2 [2 × 5 + (n - 1) × 5]
⇒ 1900 = n[10 + 5n - 5]
⇒ 1900 = n[5n + 5]
⇒ 5n2 + 5n - 1900 = 0
⇒ n2 + n - 380 = 0
⇒ n2 + 20n - 19n - 380 = 0 (on splitting the middle term)
n(n + 20) – 19(n + 20) = 0
(n – 19) (n + 20) = 0
n = 19 or – 20
But ‘n‘ cannot be negative, hence n = 19.
Hence, she continuous the savings for 19 days and saves ₹ 950.
Views on habit of saving:
(1) Child is developing a very good habit of savings.
(2) Consistent saving can create a wonder.
Q3: Write the nth term of the A.P. 1m , 1 + mm , 1 + 2mm, ....... (CBSE 2017)
 View Answer
View Answer 
Ans: Given, A.P. is 1m , 1 + mm , 1 + 2mm ......
Here, first term, a = 1/m
Common difference,
d = 1 + mm - 1m = mm = 1
∴ nth term, an = a + (n - 1)d
⇒ an = 1m + (n - 1) × 1
⇒ an = 1m + n - 1
⇒ an = mn - m + 1m
Hence, the nth term of given A.P. is: mn - m + 1m
|
127 videos|685 docs|84 tests
|
FAQs on Class 10 Maths Chapter 5 Previous Year Questions - Arithmetic Progressions
| 1. What is an arithmetic progression (AP) and how can I identify it? |  |
| 2. How do I find the nth term of an arithmetic progression? |  |
| 3. What is the formula for the sum of the first n terms of an arithmetic progression? |  |
| 4. Can you provide an example of an arithmetic progression? |  |
| 5. How can arithmetic progressions be applied in real life? |  |





















