Previous Year Questions: Context Free Language | Theory of Computation - Computer Science Engineering (CSE) PDF Download
Q1: Which of the following statements is/are CORRECT? (2023)
(a) The intersection of two regular languages is regular.
(b) The intersection of two context-free languages is context-free.
(c) The intersection of two recursive languages is recursive.
(d) The intersection of two recursively enumerable languages is recursively enumerable.
Ans: (a, b, c)
Sol:
(A) The intersection of two recursively enumerable languages is recursively enumerable. This statement is true because REL is closed under intersection operations.
(B) the intersection of two context-free languages is context-free. This statements is false.(it may or may not be closed).
Eg: Let L1 = anbncm/ m, n ≥ 0
L2 = anbmcm/ m, n ≥ 0 but
L1 ∩ L2 = anbncn/ n ≥ 0 is non-CFL language
(C) The intersection of two recursively languages is recursive. This is true because REC language is closed under intersection operations.
(D) The intersection of two regular languages is regular. This is also true.
eg: L1 = a* accept the strings like (ϵ, a, aa, aaa, aaaa.....∞)
L2 = a+ accepts the strings like (a, aa, aaa, aaaa....∞)
∴ L1 ∩ L2 = ϵ which is regular language, a finite automata with initial states is accepting states.
So option A, C, D is true where as B is false.
Q2: Consider the following languages:
L1 = {ww ∣ w ∈ {a, b}*}
L2 = {anbncm ∣ m, n ≥ 0}
L3 = {anbncn ∣ m, n ≥ 0}
Which of the following statements is/are FALSE? (2022)
(a) L1 is not context-free but L2 and L3 are deterministic context-free.
(b) Neither L1 nor L2 is context-free.
(c) L2, L3 and L2 ∩ L3 all are context-free.
(d) Neither L1 nor its complement is context-free.
Ans: (b, c, d)
Sol:
L1:
L1 = {ww} w ∣ ∈ {a, b}*
L1 is standard example of Non-Context-Free-Language. L1 is very famous language which is Non-CFL, but complement of L1 is CFL.
We can not have a PDA to recognize language L1.
Informal idea:
Informal idea is that we need to match first half of string with the second half of the string. Assume that the input string is s = abbab abbab So, we have to remember the first half of the string, so, we push the first half in the stack(PDA can non-deterministically determine the middle of the string), So, in stack we have abbab in this order with the a on bottom of the stack and the b on the top of the stack. Now, we need to match the second half of the strings with the first half, so, the first symbol of second half of string s must be matched with the first symbol of the first half. But since the first symbol of first half is on Bottom of the stack, we(PDA) cannot do this matching.
Hence, No PDA can recognize the language L1.
Formal Idea:
We can use "Pumping lemma of CFLs" to prove that L₁ is Not CFL. The proof of Non-CFLness of L1 by
"Pumping lemma of CFLs" is present in the comments of this answer.
But first, For understanding how to use Pumping lemma of CFLs to prove that a language is Non-CFL, refer my answer on the following GATE question :
L2:
L2 = {anbncm ∣n, m > = 0}
L2 is DCFL. The idea for construction of DPDA for L2 is:
Initially on the stack we have 20. Push all the a's of the input string on stack, then as soon as first b appears, start popping a's from the stack (pop one a for one b), then when the first c appears, we must have 20 on the top of the stack. If we have zo on the top of the stack when first c appears in the input string, DPDA goes to final state and consumes all the c's of the input string, without bothering the stack.
L3:
L3 = {ambncn ∣n, m > = 0}
L3 is DCFL. The idea for construction of DPDA for L3 is similar to the DPDA for L2:
Initially on the stack we have z0. Read all the a's of the input string without pushing anything on the stack (basically ignore all the a's), then as soon as first b appears, start pushing b's on the stack, then when the first c appears, start popping b's from the stack (pop one b for one c). At the end of the string, when we encounter the special "End-of-input" symbol $, we must have zo on the top of the stack. If we have zo on the top of the stack when we encounter the special "End-of-input" symbol $ in the input string, DPDA goes to final state.
L= L2 ∩ L3 = {anbncn ∣n >=0} which is another standard example of Non-Context-Free-Language. (Can be formally proved using Pumping lemma of CFLS BUT the informal idea is much simpler and intuitive)
Informal Idea:
We cannot have a PDA to recognize the language L because any PDA will have to match number of a's with number of b's, then with number of c's. BUT as soon as we match number of a's with number of b's in the input string, we(PDA) do not have any memory of number of a's in the input string to match with number of c's. So, PDA cannot recognize the language L.
Option 4:
L1 is standard example of Non-Context-Free-Language. L1 is very famous language which is Non-CFL, but complement of L1 is CFL.
Q3: Consider the following languages:
L1 = {anwan ∣w ∈ {a, b}*}
L2 = {wxwR ∣ w, x ∈ {a, b}*, ∣w∣ , ∣x∣ > 0}
Note that wR is the reversal of the string w. Which of the following is/are TRUE? (2022)
(a) L1 and L2 are regular.
(b) L1 and L2 are context-free.
(c) L1 is regular and L2 is context-free.
(d) L1 and L2 are context-free but not regular.
Ans: (a, b, c)
Sol:
L1:
If n >= 0 then the language L1 contains ALL strings i.e. L1 = {a, b}*
If n >= 1, the language L1 contains ALL and ONLY the strings that start and end with all i.e. Regular expression of L1 = a(a + b)* a
If n >= k, for some constant k, the language L1 contains ALL and ONLY the strings that start with ka's and end with ka's. i.e. Regular expression of L1 = ak(a+b)*ak, where k is some constant.
In any case, L1 is Regular. Every regular language is CFL. So, L1 is regular, as well as CFL.
In theory of computation, by default, range of any variable n can be assumed to be n >= 0. Since range of n is not given in the question, So, we can assume it to be n >= 0 (Some standard books of Theory of Computation mention that if nothing is mentioned about a variable n, then it can be assumed to be n >= 0)
L2:
L2 = {wxwR ||w| > 0, |x| > 0, w, x ∈ {a, b}*}
Every String, with at least 3 symbols, that starts and end with same symbol, is in L2 (We can take w as the first symbol, and wR will be the last symbol, remaining substring will be x)
Every string in L2 has at least 3 symbols in it and starts and ends with same symbol(We can take w as the
first symbol, and wR will be the last symbol, remaining substring will be x).
So, L2 = [a{a + b}+a] + [b{a + b}+b]
Since we have regular expression to describe L2, So, L2 is Regular, as well as CFL.
Q4: For a string w, we define wR to be the reverse of w. For example, if w = 01101 then wR= 10110.
Which of the following languages is/are context-free? (2021 SET-2)
(a) {wxwRxR | w, x ∈ {0, 1}*}
(b) {wwRxxR | w, x ∈ {0, 1}*}
(c) {wxwR | w, x ∈ {0, 1}*}
(d) {wxxRwR | w, x ∈ {0, 1}*}
Ans: (b, c, d)
Sol:
Option A: L={w x wR xR | w, x ∈ {0,1}*} This is not CFL as if we push "w" then "x" then we cannot match wR with "w" as top of stack contains x.
OptionB: L={w wR x xR | w, x ∈ {0,1}* } This is CFL. We non deterministically guess the middle of the string. So we push "w" then match with wR and again push x and match with xR
Option C: L={w x xR wR | w, x ∈ {0,1}* } This is also CFL. We non deterministically guess the middle of the string. So we push "w" then push x and then match with xR and again match with wR
Option D: L={w x wR | w, x ∈ {0,1}* } This is a regular language (hence CFL). In this language every string start and end with same symbol (as x can expand).
Q5: Let L1 be a regular language and L2 be a context-free language. Which of the following languages is/are context-free? (2021 SET-2)
(a) 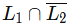
(b)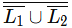
(c)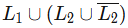
(d)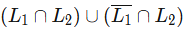
Ans: (b, c, d)
Sol:
The options should be b, c, d.
Options -
(a) The Complement of CFL is Recursive. The intersection of Recursive and Regular is Recursive.
(b) It is L1 ∩ L2 and intersection of CFL and regular is CFL.
(c) It is ∑* itself as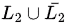 is ∑* and union of " and L1 is ∑* which is regular and thus CFL
is ∑* and union of " and L1 is ∑* which is regular and thus CFL
(d) Solving this you will get L2 which is CFL. See the image below.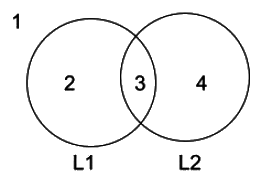
We can write the (d) option as,
= (23 ∩ 34) U (14 ∩ 34)
= (3) U (4)
=L2
Q6: Suppose that L1 is a regular language and L2 is a context-free language. Which one of the following languages is NOT necessarily context-free? (2021 SET-1)
(a) L1 ∩ L2
(b) L1 . L2
(c) L1 - L2
(d) L1 ∪ L2
Ans: (c)
Sol:
Given,
- L1 - Regular Language (RL)
- L2 - Context-Free Language (CFL)
(A) L1 ∩ L2 → CFL
Because intersection operation with regular languages is closed under CFLs.
Hence, True.
(B) L1 . L2 → CFL
Every regular language is a CFL and CFLs are closed under concatenation.
Hence, True.
(C)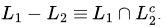
Suppose, let's consider L1 = ∑* and L2 as any CFL and we get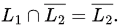
Since CFLs aren't closed under complementation, this means L1 - L2 NEED NOT be a CFL!
Hence, False.
(D) L1 U L2 → CFL
Since CFLs are closed under union operation and a regular language is also a CFL.
Hence, True.
Q7: Consider the following languages.
L1 = {wxyx ∣ w,x,y ∈ (0 + 1)+}
L2 = {xy ∣ x, y ∈ (a + b)*, ∣x∣ = ∣y∣ , x ≠ y}
Which one of the following is TRUE? (2020)
(a) L1 is regular and L2 is context- free.
(b) L1 context-free but not regular and L2 is context-free.
(c) Neither L1 nor L2 is context- free.
(d) L1 context-free but L2 is not context-free.
Ans: (a)
Sol:
Here for L1 a regular expression exists,
L1 = (0 + 1)+0(0 + 1)+0 + (0 + 1)+1(0 + 1)+1
So, L1 is a Regular Language.
Now, for L2 a context-free grammar exists which is shown below,
- S → AB | BA
- A → a | aAa | aAb | bAb | baa
- B → b | aBa | aBb | bBb | bBa
L2 is the complement of L = {ww | w ∈ (a + b)*} ∪ {w | w ∈ (a + b)* and |w| is odd }
So correct option is : A
Q8: Consider the language L = {an | n ≥ 0} ∪ {anbn | n ≥ 0} and the following statements.
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE? (2020)
(a) I only
(b) II only
(c) I and III only
(d) III only
Ans: (c)
Sol: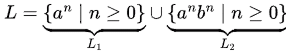
Here, L1 is a regular language having regular expression a* and L2 is a DCFL. DCFL is closed under union operator with a regular language as shown below.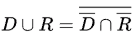
Since, DCFL and regular sets are closed under complement this gives a DCFL intersection a regular language and DCFL is closed under intersection with regular set.
So, L must be deterministic context-free.
LL(k) parser needs to determine the next grammar production by seeing the next k input symbols. Now, if we have a string like ak+1 ..., the parser has no idea whether to pick the production for an or anbn. i.e., the input string can be either say ak+10 or ak+10 bk+10, and the LL(k) parser (whatever LL(k) grammar we use for the given language) cannot determine which one it is and so gets stuck. So, the given language is not LL(k) for any k.
Q9: Which one of the following languages over ∑ = {a, b} is NOT context-free? (2019)
(a) {wwR | w ∈ {a, b}*}
(b) {wanbnwR | w ∈ {a, b}*, n ≥ 0}
(c) {wanwRbn | w ∈ {a, b}*, n ≥ 0}
(d) {anbi l i ∈ {n, 3n, 5n}, n ≥ 0}
Ans: (c)
Sol:
- {wanbnwR [w ∈ (a, b)*, n ≥ 0} is accepted by a non-deterministic pushdown automaton and hence it is a context-free language
- {wwR [w ∈ {a, b}*} is accepted by a non-deterministic pushdown automaton and hence it is context-free language.
- {wan wRbn/w ∈ (a, b)*, n ≥ 0} is not accepted by a pushdown automaton and hence it is not a context-free language.
- i = n, 2n, 3n, 4n, etc. forms and arithmetic series. anbn, anb2n and anb3n is accepted by a deterministic pushdown automaton and context-free language are closed under union and hence anbn ∪ anb2n ∪ anb3n is a context-free language. |
Hence (anbi li ∈ {n, 3n, 5n), n ≥ 0} is a context-free language.
Q10: Consider the following languages:
I. {ambncpdq ∣ m + p = n + q, where m, n, p, q ≥ 0}
II. {ambncpdq ∣ m = n and p = q, where m, n, p, q ≥ 0}
III. {ambncpdq ∣ m = n = p and p ≠ q, where m, n, p, q ≥ 0}
IV. {ambncpdq ∣ mn = p + q, where m, n, p, q ≥ 0}
Which of the languages above are context-free? (2018)
(a) I and IV only
(b) I and II only
(c) II and III only
(d) II and IV only
Ans: (b)
Sol:
I) {ambncpdq ∣ m + p = n + q, where m, n, p, q ≥ 0}
Grammar :
S → aSd | ABC | ∈
A → aAb | ab | ∈
B → bBc | bc | ∈
C → cCd | cd | ∈
II) {ambncpdq ∣ m = n and p = q, where m, n, p, q ≥ 0}
S → ABC | ∈
A → aAb | ab
B → cBd | cd
Above Grammar is CFG so it will generate CFL.
III) {ambncpdq ∣ m = n = p and p ≠ q, where m, n, p, q ≥ 0}
More than one comparison so NOT CFL.
IV) {ambncpdq ∣ mn = p + q, where m, n, p, q ≥ 0}
It is CSL but NOT CFL.
Correct Answer:
Q11: Consider the following languages
L1 = {ap | p is a prime number}
L2 = {anbmc2m | n ≥ 0, m ≥ 0}
L3 = {anbnc2n | n ≥ 0}
L4 = {anbn | n ≥ 1}
Which of the following are CORRECT ? (2017 SET-2)
I.L1 is context-free but not regular.
II. L2 is not context-free.
III. L3 is not context-free but recursive.
IV. L4 is deterministic context-free.
(a) I,II and IV only
(b) II and III only
(c) I and IV only
(d) III and IV only
Ans: (d)
Sol:
L1 is Csl, L2 is context free
L3 is not Context free and L4 is Dcfl
So, option is D.
Q12: Let L1, L2 be any two context free languages and R be any regular language.
Then which of the following is/are CORRECT ? (2017 SET-2)
I. L1 U L2 is context - free
II.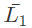 is context - free
is context - free
III. L1 − R is context - free
IV. L1 ∩ L2 is context - free
(a) I, II and IV only
(b) I and III only
(c) II and IV only
(d) I only
Ans: (b)
Sol:
Statement I is TRUE as CFGs are closed under union.
Statement II is FALSE as CFGs are not enclosed under complementation.
Statement III is TRUE as L1 − R can be written as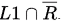 Regular language are closed under complementation and intersection of CFG and Regular is CFG.
Regular language are closed under complementation and intersection of CFG and Regular is CFG.
Statement IV is FALSE as CFGs are not enclosed under intersection.
So, I and III are correct. Option B.
Q13: Consider the following languages over the alphabet ∑ = {a, b, c}.
Let L1 = {anbncm ∣ m, n ≥ 0} and L2 = {ambncn ∣ m, n ≥ 0}
Which of the following are context-free languages ? (2017 SET-1)
I. L1 ∪ L2
II. L1 ∩ L2
(a) I only
(b) II only
(c) I and II
(d) Neither I nor II
Ans: (a)
Sol:
Correct Option: A
- Here, let's say L = L1 U L2
Here as we see, L1 and L2 both are DCFLs. And hence CFLs.
And from the Closure Properties of CFLs, we can conclude that CFLs are Closed under Union
Operation.
And hence, L = L1 U L2 is CFL. - Now, let's take L = L1 ∩ L2, and that can be expressed as,
L = {aibjck | i = j AND j = k, i, j, k ≥ 0}, in other words
L = {anbncn | n ≥ 0}
And we know that it comes under CSL (As we will require Two Stacks at a Time). So L is CSL and also NOT a CFL.
Q14: Consider the context-free grammars over the alphabet {a,b,c} given below. S and T are non-terminals (2017 SET-1)
G1 : S → aSb | T,T | CT | ϵ G2 : S → bSa | T, T → CT | ϵ
The language L(G1) ∩ L(G2) is
(a) Finite.
(b) Not finite but regular.
(c) Context-free but not regular.
(d) Recursive but not context-free.
Ans: (b)
Sol:
Since while intersection all strings produced by production aSb in G1 and bSa in G2 will be 0
So, only common production will be:
S → T
T → cT | ϵ
Which is nothing but c* hence it is REGULAR and INFINITE
So, option is (B).
Q15: Consider the following languages: (2016 SET-2)
L1 = {anbmcn+m : m, n ≥ 1}
L2 = {anbnc2n : n ≥ 1}
Which one of the following is TRUE?
(a) Both L1 and L2 are context-free.
(b) L1 is context-free while L2 is not context-free.
(c) L2 is context-free while L1 is not context-free.
(d) Neither L1 nor L2 is context-free.
Ans: (b)
Sol:
L1 = {anbmcn+m : m, n ≥ 1} is Context-free language
(push a's into stack, then push b's into stack, read c's and pop b's, when no b's left on stack, keep reading c's and pop a's, when no c's left in input, and stack is empty, then accepted).
L2 = {anbnc2n : n ≥ 1} is Context-sensitive language and not context-free. (cannot implemented by one stack)
So, answer is option B.
Q16: Consider the following types of languages: L1: Regular, L2: Context-free, L3: Recursive, L4: Recursively enumerable.
Which of the following is/are TRUE? (2016 SET-2)
I.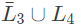 is recursively enumerable
is recursively enumerable
II.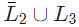 is recursive
is recursive
III.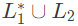 is context-free
is context-free
IV.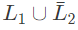 is context-free
is context-free
(a) I only
(b) I and III only
(c) I and IV only
(d) I, II and III only
Ans: (d)
Sol: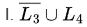
L3 is recursive, so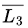 is also recursive (closed under complement),
is also recursive (closed under complement),
So,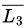 is recursive enumerable.L4 is recursive enumerable,
is recursive enumerable.L4 is recursive enumerable,
so,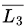 U L4 is also recursive enumerable (closed under union).
U L4 is also recursive enumerable (closed under union).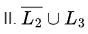
L2 is Context-free, so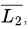 may or may not be Context-free (not closed under complement), but definitely
may or may not be Context-free (not closed under complement), but definitely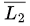 is Recursive.
is Recursive.
L3 is recursive.
so 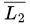 U L3 is also recursive (closed under union).
U L3 is also recursive (closed under union).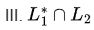
L1 is Regular, so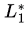 is also regular (closed under kleene star)
is also regular (closed under kleene star)
L2 is Context-free
so, 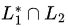 is also context-free (closed under intersection with regular).
is also context-free (closed under intersection with regular).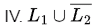
L1 is regular.
L2 is context-free, so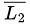 may or may not be Context-free (not closed under complement).
may or may not be Context-free (not closed under complement).
so,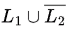 may or may not be Context-free.
may or may not be Context-free.
Here, answer is D.
Q17: Which of the following languages are context-free? (2015 SET-3)
L1 = {ambnanbm | m, n ≥ 1}
L2 = {ambnambn | m, n ≥ 1}
L3 = {ambn | m = 2n + 1}
(a) L1 and L2 only
(b) L1 and L3 only
(c) L2 and L3 only
(d) L3 only
Ans: (b)
Sol:
first check for L1. now look am & bm and an & bn must be comparable using one stack for CFL.
now take a stack push all am in to the stack then push all bn in to stack now an is coming so pop bn for each an by this bn and an will b comparable. now we have left only am in stack and bm is coming so pop am for each bm by which we can compare am to bm we conclude that we are comparing this L1 using a single stack so this is CFG.
now for L2. this can not be done in to a single stack because m and n are not comparable we can not find when to push or pop so this is CSL.
now for L3.push all a's into stack and pop 2a 's for every b and at last we left with a single a because here aaaaabb is a valid string where m = 2n + 1 and n = 2. So realized using single stack hence L3 is CFG.
so the option is B.. L1 and L3 are CFG
Q18: For any two languages L1 and L2 such that L1 is context-free and L2 is recursively enumerable but not recursive, which of the following is/are necessarily true? (2015 SET-1)
I.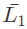 (complement of L1) is recursive
(complement of L1) is recursive
II.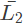 (complement of L2) is recursive
(complement of L2) is recursive
III.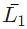 is context-free
is context-free
IV.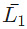 U L2 is recursively enumerable
U L2 is recursively enumerable
(a) I only
(b) III only
(c) III and IV only
(d) I and IV only
Ans: (d)
Sol:
L1 is context-free and hence recursive also. Recursive set being closed under complement, L1' will be recursive.
L1' being recursive it is also recursively enumerable and Recursively Enumerable set is closed under Union. So, L1 U L2 is recursively enumerable.
Context free languages are not closed under complement, so III is false
Recursive set is closed under complement. So, if L2' is recursive, (L2') = L2 is also recursive which is not the case here. So, II is also false.
Q19: Consider the following languages over the alphabet ∑ = {0, 1, c} :
L1 = {0n ∣ 1n ∣ n ≥ 0}
L2 = {wcwr ∣ w ∈ {0,1}*}
L3 = {wwr ∣ w ∈ {0,1}*}
Here wr is the reverse of the string w. Which of these languages are deterministic Context free languages? (2014 SET-3)
(a) None of the languages
(b) Only L1
(c) Only L1 and L2
(d) All the three languages
Ans: (c)
Sol:
For the languages L1 & L2 we can have deterministic push down automata, so they are DCFL's, but for L3 only non-deterministic PDA possible. So the language L3 is not a deterministic CFL.
Q20: Consider the following languages. L1 = {0p1q0r ∣ p, q, r ≥ 0}
L2 = {0p1q0r ∣ p, q, r ≥ 0, p ≠ r}
Which one of the following statements is FALSE? (2013)
(a) L2 is context-free
(b) L1 ∩ L2 is context-free
(c) Complement of L2 is recursive.
(d) Complement of L1 is context-free but not regular
Ans: (d)
Sol:
L1 is regular and hence context-free also. Regular expression for L1 is 0*1*0*. So, (D) is the false choice.
L2 is context-free but not regular. We need a stack to count if the number of O's before and after the 1 (1 may be absent also) are not same. So, L1 ∩ L2 is context-free as regular context-free is context-free. → (B) is true.
Complement of L2 is recursive as context-free complement is always recursive (actually even context-sensitive).
Q21: Consider the languages L1, L2 and L3 as given below
L1 = {0p1q ∣ p, q ∈ N}
L2 = {0p1q ∣ p, q ∈ Nandp = q} and
L3 = {0p1q0r ∣ p, q, r ∈ N and p = q = r}
Which of the following statements is NOT TRUE? (2011)
(a) Push Down Automata (PDA) can be used to recognize L1 and L2
(b) L1 is a regular language
(c) All the three languages are context free
(d) Turing machines can be used to recognize all the languages
Ans: (c)
Sol:
L1 is Regular(no stack is required, it has a DFA) so obviously it is CFL
L2 requires one stack so it is CFL
L3 more than one stack is required-CSL
And every RL, CFL, CSL are Recursively Enumerable so accepted by TMs.
So C is answer
Q22: Consider the languages
L1 = {0i1j | i ≠ j}.
L2 = {0i1j | i = j}.
L3 = {0i1j | i = 2j +1}.
L4 = {0i1j | i ≠ 2j}
Which one of the following statements is true? (2010)
(a) Only L2 is context free
(b) Only L2 and L3 are context free
(c) Only L1 and L3 are context free
(d) All are context free
Ans: (d)
Sol:
Correct Answer: D. All are context free.
L1 Push 0 on stack and when 1 comes, start popping. If stack becomes empty and 1's are remaining start
pushing 1. At end of string accept if stack is non- empty.
L2 → Do the same as for L1, but accept if stack is empty at end of string.
L3 → Do, the same as for L2, but for each 0, push two 0's on stack and start the stack with a 0.
L4 → Do the same as for L1, but for each 0, push two 0's on stack
All are in fact DCFL. Pushing two 0's on stack might sound non-trivial but we can do this by pushing one symbol and going to a new state. Then on this new state on empty symbol, push one more symbol on stack and come back.
|
18 videos|93 docs|44 tests
|
FAQs on Previous Year Questions: Context Free Language - Theory of Computation - Computer Science Engineering (CSE)
| 1. What is a context-free language in computer science? |  |
| 2. What are some examples of context-free languages? |  |
| 3. How can context-free languages be recognized by computers? |  |
| 4. What is the difference between a context-free language and a regular language? |  |
| 5. Why are context-free languages important in computer science? |  |
















