Class 10 Maths Chapter 8 Previous Year Questions - Introduction to Trigonometry
Previous Year Questions 2024
Q1: If sin α = √3/2 , cos β = √3/2 then tan α. tan β is: (CBSE 2024)(a) √3
(b) 1/√3
(c) 1
(d) 0
 View Answer
View AnswerAns: (c)
sin α = √3/2, ⇒ sin α = sin 60º
⇒ α = 60º
∵ cos β = √3/2,
⇒ cos β = cos 30º
⇒ β = 30º
tan α. tan β = tan 60º. tan 30º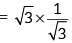
= 1
Q2: Evaluate: 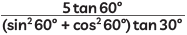 (CBSE 2024)
(CBSE 2024)
 View Answer
View AnswerAns: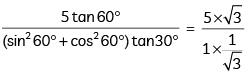
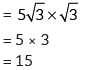
Q3: Prove that: (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) = 1 (CBSE 2024)
 View Answer
View AnswerAns:
L.H.S. = (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ)
= (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ)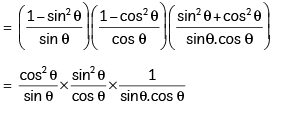
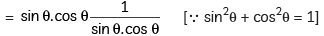
= 1 = R.H.S.
Hence, proved.
Previous Year Questions 2023
Q4: If 2 tan A = 3, then find the value of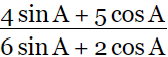 is (2023)
is (2023) View Answer
View AnswerAns: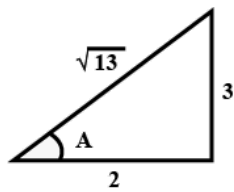
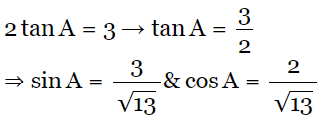

Hence, the answer is 1.
Q5: 5/8 sec260° - tan260° + cos245° is equal to (2023)
(a) 5/3
(b) -1/2
(c) 0
(d) -1/4
 View Answer
View AnswerAns: (c)
Sol: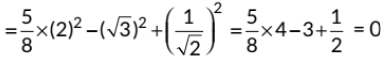
Q6: Evaluate 2 sec2θ + 3 cosec2θ - 2 sin θ cos θ if θ = 45° (CBSE 2023)
 View Answer
View AnswerAns: Since θ = 45°, sec 45° = √2, cosec 45° = √2, sin 45° = 1/√2 cos 45° = 1/√2
2sec2 θ + 3 cosec2 θ – 2 sin θ cos θ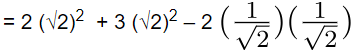
= 4 + 6 – 1 = 9
Q7: Which of the following is true for all values of θ(0o ≤ θ ≤ 90o)? (2023)
(a) cos2θ - sin2θ - 1
(b) cosec2θ - sec2θ- 1
(c) sec2θ - tan2θ - 1
(d) cot2θ- tan2θ = 1
 View Answer
View AnswerAns: (c)
Q8: If sinθ +cosθ = √3. then find the value of sinθ . cosθ. (2023)
 View Answer
View AnswerAns: Given, sinθ +cosθ = √3
Squaring both sides, we get (sinθ + cosθ)2 = 3
⇒ sin2θ + cos2θ + 2sinθ cosθ = 3
⇒ 2sinθ cosθ = 3 - 1 ( ∵ sin2θ + cos2θ = 1)
⇒ 2sinθ cosθ = 2
⇒ sinθ cosθ = 1
Q9: If sin α = 1/√2 and cot β = √3, then find the value of cosec α + cosec β. (2023)
 View Answer
View AnswerAns: Given, sin α = 1/√2 and cot β = √3
We know that, cosec α = 1/sinα = √2
Also, 1 + cot2β = cosec2β
⇒ cosec2β = 4
⇒ cosec β = 4
Now, cosec α + cosec β = √2 + 2
Q10: Prove that the Following Identities: Sec A (1 + Sin A) ( Sec A - tan A) = 1 (2023)
 View Answer
View AnswerAns: LHS = sec A(1 + sin A )( sec A - tan A)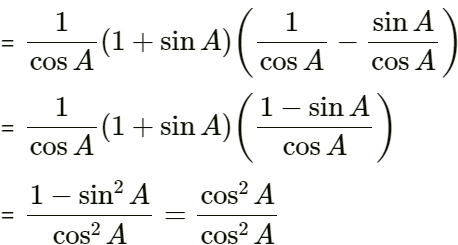
= 1
= RHS
Hence proved..
Q11: (sec2 θ – 1) (cosec2 θ – 1) is equal to:
(a) –1
(b) 1
(c) 0
(d) 2 (CBSE 2023)
 View Answer
View AnswerAns: (b)
(sec2 θ – 1) (cosec2 θ – 1) = tan2 θ.cot2 θ 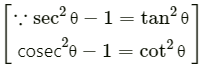
= 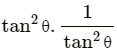
= 1
Q12: If sin θ – cos θ = 0, then find the value of sin4 θ + cos4 θ. (CBSE 2023)
 View Answer
View AnswerAns: Given,
sin θ – cos θ = 0
sin θ = cos θ
tan θ = 1
tan θ = tan 45°
⇒ θ = 45°
Now, sin4 θ + cos4 θ = sin4 45° + cos4 45°
Q13: Prove that 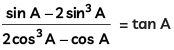 (CBSE 2023)
(CBSE 2023)
 View Answer
View AnswerAns: 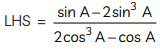
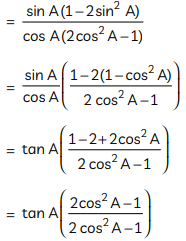
= tan A
= RHS
Previous Year Questions 2022
Q14: Given that cos θ = √3/2, then the value of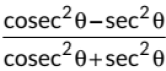 is (2022)
is (2022)(a) -1
(b) 1
(c) 1/2
(d) -1/2
 View Answer
View AnswerAns: (c)
Sol:
Given, cosθ = √3/2 = B/H
Let B = √3k and H = 2k
∴  [By Pythagoras Theorem]
[By Pythagoras Theorem]
⇒√k2 = k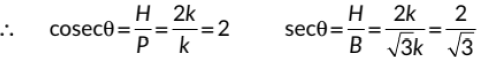
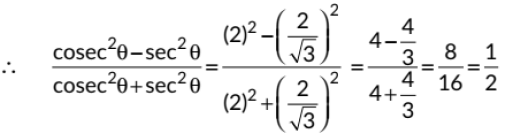
Q15: 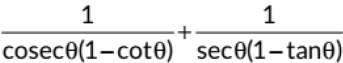 is equal to (2022)
is equal to (2022)
(a) 0
(b) 1
(c) sinθ + cosθ
(d) sinθ - cosθ
 View Answer
View AnswerAns: (c)
Sol: We have,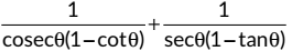
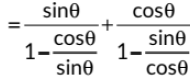
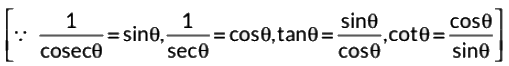
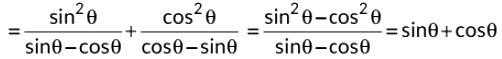
Q16: The value of θ for which 2 sin2θ = 1, is (2022)
(a) 15°
(b) 30°
(c) 45°
(d) 60°
 View Answer
View AnswerAns: (a)
Sol: Given, 2 sin2θ = 1 ⇒ sin2θ = 1/2
⇒ 2θ = 30°
⇒ θ = 15°
Q17: If sin2θ + sinθ = 1, then find the value of cos2θ + cos4θ is (2022)
(a) -1
(b) 1
(c) 0
(d) 2
 View Answer
View AnswerAns: (b)
Sol: Given, sin2θ + sinθ = 1 ---(i)
sinθ = 1 - sin2θ
⇒ sinθ = cos2θ ---(ii)
∴ cos2θ + cos4θ
= sinθ + sin2θ [From (ii)]
= 1 [From (i)]
Previous Year Questions 2021
Q18: If 3 sin A = 1. then find the value of sec A. (2021 C) View Answer
View AnswerAns: We have, 3 sin A = 1
∴ sin A = 1/3
Now by using cos2 A = 1 - sin2 A, we get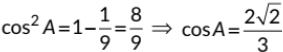
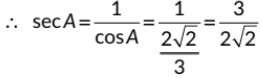
Q19: Show that: 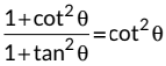 (2021 C)
(2021 C)
 View Answer
View AnswerAns: We have, L.H.S.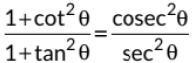
[By using 1 + tan2θ = sec2θ and 1 + cot2 θ = cosec2θ ]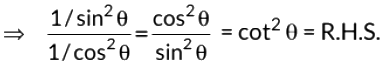
Hence,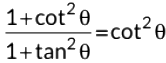
Previous Year Questions 2020
Q20: If sin θ = cos θ, then the value of tan2 θ + cot2 θ is (2020)(a) 2
(b) 4
(c) 1
(d) 10/3
 View Answer
View AnswerAns: (a)
Sol: We have, sin θ = cos θ
or sin θ / cos θ = 1
⇒ tan θ = 1 and cot θ = 1 [∵ cot θ = 1/tanθ]
∴ tan2 θ + cot2 θ = 12 + 12 = 2
Hence, A option is correct.
Q21: Given 15 cot A = 8, then find the values of sin A and sec A. (2020)
 View Answer
View AnswerAns: In right angle ΔABC we have
15 cot A = 8
⇒ cot A = 8/15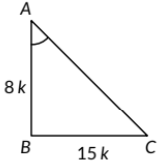
Since, cot A = AB/BC
∴ AB/BC = 8/15
Let AB = 8k and BC = 15k
By using Pythagoras theorem, we get
AC2 = AB2 + BC2
⇒ (8k)2 + (15)2 = 64k2 + 225k2 = 289k2 = (17k)2 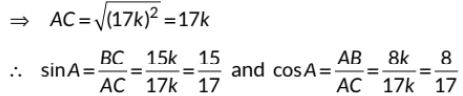
So, sec A = 1/cosA = 17/8
Q22: Write the value of sin2 30° + cos2 60°. (2020)
 View Answer
View AnswerAns: We have, sin2 30° + cos2 60°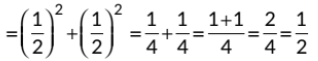
Q23: The distance between the points (a cos θ + b sin θ, 0) and (0, a sin θ − b cos θ) is (2020)
(a) a2 + b2
(b) a + b
(c) 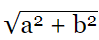
(d) 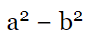
 View Answer
View AnswerAns: (c)
Sol: Given the point A (cos θ + b sin θ , 0), (0 , a sin θ − b cos θ)
By distance formula,
The distance of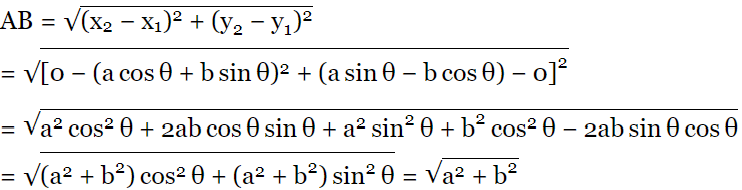
[∵ cos2θ + sin2θ = 1]
Q24: 5 tan2θ - 5 sec2θ = ____________. (2020)
 View Answer
View AnswerAns: We have 5(tan2θ - sec2θ)
= 5(-1) = - 5 [By using 1 + tan2θ = sec2 θ ⇒ tan2θ - sec2θ = - 1]
Q25: If sinθ + cosθ = √3. then prove that tan θ + cot θ = 1 (2020)
 View Answer
View AnswerAns: sin θ + cos θ =√3
= (sinθ + cosθ)2 = 3
= sin2 θ + cos2 θ + 2sin θ cos θ = 3
⇒ 2sin θ cos θ = 2
⇒ sin θ cos θ = 1
⇒ sin θ cos θ = sin2θ + cos2θ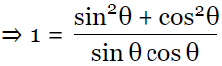
⇒ tan θ + cot θ = 1
Q26: If x = a sinθ and y = b cosθ , write the value of (b2x2 + a2y2). (CBSE 2020)
 View Answer
View AnswerAns: Given, x = a sin θ and y = b cos θ
b2x2 + a2y2 = b2(a2 sin2 θ) + a2(b2 cos2 θ)
= a2b2 [sin2 θ + cos2 θ]
= a2b2 [sin2θ + cos2θ = 1]
Q27: Prove that: 2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1 = 0. (CBSE 2020)
 View Answer
View AnswerAns: We know that,
sin2 θ + cos2 θ = 1
So, (sin2 θ + cos2 θ) 2 = 12
⇒ sin4 θ + cos4 θ + 2sin2 θ cos2 θ = 1
i.e., sin4 θ + cos4 θ = 1 – 2 sin2 θ cos2 θ …(i)
Also, (sin2 θ + cos2 θ) 3 = 13
⇒ sin6 θ + cos6 θ + 3 sin2 θ cos2 θ (sin2 θ + cos2 θ) = 1
⇒ sin6 θ+ cos6 θ+ 3sin2 θ cos2 θ (1) = 1
i.e., sin6 θ + cos6 θ = 1 – 3 sin2 θ cos2 θ …(ii)
Now,
LHS = 2(sin6 θ + cos6 θ) – 3(sin4 θ + cos4 θ) + 1
= 2(1 – 3 sin2 θ cos2 θ) – 3(1 – 2 sin2 θ cos2 θ) + 1
= 2 – 3 + 1
= 0
Hence, proved.
Q28: Prove that: (sin4 θ – cos4 θ + 1) cosec2 θ = 2. [CBSE 2020].
 View Answer
View AnswerAns: L.H.S. = (sin4 θ – cos4 θ + 1) cosec2 θ
= [(sin2 θ + cos2 θ) (sin2 θ – cos2 θ) + 1] cosec2 θ
[(1) (sin2 θ – cos2 θ) + 1] cosec2 θ as [ sin2 θ + cos2 θ = 1]
= [sin2 θ + (1 – cos2 θ)] cosec2 θ
= (sin2 θ + sin2 θ) cosec2θ
= (2 sin2 θ) cosec2 θ
= 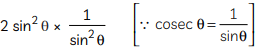
= 2 × 1
= 2 = R.H.S.
Hence, proved.
Previous Year Questions 2019
Q29: If sin x + cos y = 1, x = 30° and y is acute angle, find the value of y. (2019) View Answer
View AnswerAns: Given,
⇒ sin x + cos y = 1
⇒ sin 30° + cos y = 1
⇒ 1/2 + cos y = 1
⇒ cos y = 1 - 1/2
⇒ cos y = 1/2
⇒ cos y = cos 60°.
Hence, y = 60°.
Q30: If cosec2 θ (cos θ - 1)(1 + cos θ) = k, then what is the value of k? (2019)
 View Answer
View AnswerAns: Given:
cosec2 θ (cos θ - 1)(1 + cos θ) = k
Concept used:
Cosec α = 1/Sin α
Sin2 α + Cos2 α = 1
(a + b)(a - b) = a2 - b2
Calculation:
cosec2 θ (cos θ - 1)(1 + cos θ) = k
⇒ cosec2 θ (1 - cos θ)(1 + cos θ) = -k
⇒ cosec2 θ (1 - cos2 θ) = -k
⇒ cosec2 θ × sin2 θ = -k
⇒ 1 = -k
⇒ k = -1
∴ The value of k is (-1).
Q31: The value of ( 1 + cot A − cosec A ) ( 1 + tan A + sec A ) is
 View Answer
View AnswerAns: 
Previous Year Questions 2013
Q32: If sec θ + tan θ + 1 = 0, then sec θ – tan θ is:(a) –1
(b) 1
(c) 0
(d) 2 (CBSE 2013)
 View Answer
View AnswerAns: (a)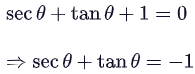
Multiplying and dividing LHS by sec θ – tan θ
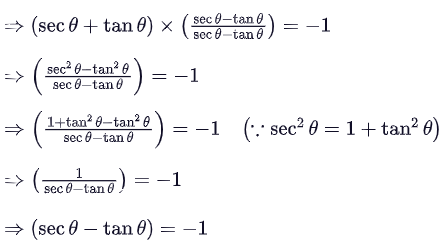
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 8 Previous Year Questions - Introduction to Trigonometry
| 1. What are the basic trigonometric ratios I need to know for Grade 10? |  |
| 2. How can I remember the trigonometric ratios easily? |  |
| 3. How do I solve problems involving the sine rule in trigonometry? |  |
| 4. What is the difference between sine, cosine, and tangent functions? |  |
| 5. How can I apply trigonometry in real-life situations? |  |

|
Explore Courses for Class 10 exam
|

|


















