Previous Year Questions: Triangles | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Previous Year Questions 2024 |

|
| Previous Year Questions 2023 |

|
| Previous Year Questions 2022 |

|
| Previous Year Questions 2021 |

|
| Previous Year Questions 2020 |

|
| Previous Year Questions 2019 |

|
Previous Year Questions 2024
Q1: In ΔABC, DE || BC (as shown in the figure). If AD = 2 cm, BD = 3 cm, BC = 7.5 cm, then the length of DE (in cm) is: (CBSE 2024) (a) 2.5
(a) 2.5
(b) 3
(c) 5
(d) 6
 View Answer
View AnswerAns: (b)  In ΔABC, DE || BC
In ΔABC, DE || BC
AD = 2 cm
BD = 3 cm
∴ AB = AB + BD
= (2 + 3) cm
AB = 5 cm
Now, ∠ADE = ∠ABC, ∠AED = ∠ACB [Corresponding angles]
So by AA prop. ΔADE ∼ ΔABC
⇒ AD/AB = DE/BC
⇒ 2/5 = DE/7.5

 DE = 3 cm
DE = 3 cm
Q2: In ΔABC, if AD ⊥ BC and AD2 = BD × DC, then prove that ∠BAC = 90º. (CBSE 2024)
 View Answer
View AnswerAns: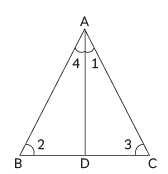
Here,
AD ⊥ BC
and
AD2 = BD × DC
i.e., AD × AD = BD × DC
AD/DC = BD/AD (transposing)
and ∠ADB = ∠CDA [Each 90°]
⇒ ∆ADB ~ ∆CDA
∠1 = ∠2 [By CPST]
∠3 = ∠4 (i)
In ∆AD C,
∠3 + ∠ADC + ∠1 = 180°
∠3 + 90° + ∠1 = 180°
∠1 = 180° – 90° – ∠3
∠1 = 90° – ∠3
∠BAC = ∠1 + ∠4
= 90° – ∠3 + ∠3
[∵∠4 = ∠3 From eqn. (i)]
i.e., ∠BAC = 90°
Hence, Proved
Previous Year Questions 2023
Q3: in ΔABC, PQ || BC If PB = 6 cm, AP = 4 cm, AQ = 8 cm. find the length of AC. (2023) (a ) 12 cm
(a ) 12 cm (b) 20 cm
(c) 6 cm
(d) 14 cm
 View Answer
View AnswerAns: (b)
Sol: Since, PQ || BC
∴ 
⇒ 
= 12 cm
Q4: In the given figure, XZ is parallel to BC. AZ = 3 cm, ZC = 2 cm, BM = 3 cm and MC = 5 cm. Find the length of XY. (2023)
 View Answer
View AnswerAns: Given, AZ = 3 cm, ZC = 2 cm. BM = 3 cm and MC = 5 cm
In ΔABC, XZ || BC
Now, AC = AZ + ZC = 3 + 2 = 5cm
BC = BM + MC = 3 + 5 = 8 cm and
In ΔAXY and ΔABM
∠AXY = ∠ABM (Corresponding angles are equal as XZ || BC)
∠XAY = ∠BAM (Common)
∴ ΔAXY ∼ ΔABM (By AA similarity criterion)
(Corresponding sides of similar triangles)
From (i) and (ii), we get (By Basic Proportionality Theorem)
(By Basic Proportionality Theorem)
= 1.8cm
Q5: Assertion (A) : The perimeter of ΔABC is a rational number.
Reason (R) : The sum of the squares of two rational numbers is always rational. (2023)
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
 View Answer
View AnswerAns: (d)
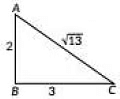
In ΔABC, AC2 = AB2 + BC2
⇒ AC2 = 22 + 32
⇒ AC2 = 4 + 9
⇒ AC= √13 cm
So, perimeter is (2 + 3 + √13)cm = (5 + √13), which is irrational.
Hence, Assertion in false but Reason is true.
Q6: In a ΔPQR, N is a point on PR, such that QN ⊥ PR. If PN × NR = QN2, prove that ∠PQR = 90°. (CBSE 2023)
 View Answer
View AnswerAns: In ΔPQR, QN ⊥ PR and PN × NR = QN2 In ΔQNP and ΔRNQ,
In ΔQNP and ΔRNQ,
∠1 = ∠2 = 90°
QN2 = NR × NP (Given)
QN × QN = NR × NP
QN / NR = NP / QN
∴ ΔQNP ~ΔRNQ (By SAS similarity criterion)
∠P = ∠RQN = x …(i)
∠PQN = ∠R = ∠y …(ii)
In ΔPQR, we have
∠P + ∠PQR + ∠R = 180º
∠x + ∠x + ∠y + ∠y = 180º
2∠x + 2∠y = 180º
2(∠x + ∠y) = 180°
∠x + ∠y = 90º
∠PQR = 90º,
Hence, proved
Q7: In the given figure, ΔABC and ΔDBC are on the same base BC. If AD intersects BC at O, prove that  . (CBSE 2023)
. (CBSE 2023)

 View Answer
View AnswerAns: Given: ΔABC and ΔDBC are on the same base BC. AD and BC intersect at O.
To Prove:
Construction: Draw AL ⊥ BC and DM ⊥ BC
Now, in ΔALO and ΔDMO, we have
∠ALO = ∠DMO = 90°
∠AOL = ∠DOM (Vertically opposite angles)
Therefore, ΔALO ~ ΔDMO
∴  (Corresponding sides of similar triangles are proportional)
(Corresponding sides of similar triangles are proportional)
Hence, proved.
Q8: In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm, and BQ = 5 cm, then the length of BC is ______.
(a) 8 cm
(b) 3 cm
(c) 0.3 cm
(d) 25/3 cm (CBSE 2023)
 View Answer
View AnswerAns: (a)
As PQ || AC by using basic proportionality theorem
QC = 3 cm
∴ BC = BQ + QC
= 5 + 3
= 8 cm
Previous Year Questions 2022
Q9: In the figure given below, what value of x will make PQ || AB? (2022) (a) 2
(a) 2
(b) 3
(c) 4
(d) 5
 View Answer
View AnswerAns: (a)
Sol: Suppose PQ || AB
By Basic Proportionality theorem we have
⇒ 6x = 12
⇒ x = 2
So, for x = 2, PQ IIAB
Q10: If Δ ABC and Δ PQR are similar triangles such that ∠A = 31° and ∠R = 69°, then ∠Q is : (2022)
(a) 70°
(b) 100°
(c) 90°
(d) 80°
 View Answer
View AnswerAns: (d)
Sol: Given Δ ABC and Δ PQR are similar.
Hence, ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R
We know that,
∠P + ∠Q + ∠R = 180°
31° + ∠Q + 69° = 180°
100° + ∠Q = 180°
∠Q = 180° - 100°
∠Q = 80°
Q11: A vertical pole of length 19 m casts a shadow 57 m long on the ground and at the same time a tower casts a shadow 51m long. The height of the tower is (2022)
(a) 171m
(b) 13 m
(c) 17 m
(d) 117 m
 View Answer
View AnswerAns: (c)
Sol: Let AB be the pole and PQ be the tower
Let height of tower be h m
Now, ΔABC ∼ ΔPQR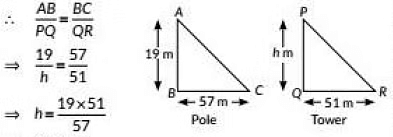
⇒ h = 17m
Previous Year Questions 2021
Q12: Aman goes 5 metres due west and then 12 metres due North. How far is he from the starting point? (2021) View Answer
View AnswerAns: 13 m
Let Aman starts from A point and continues 5 m towards west and readied at B point, from which he goes 12 m towards North reached at C point finally.
In ΔABC, we have
AC2 = AB2 + BC2 [By Pythagoras theorem]
AC2 = 52 + 122
AC2 = 25 + 144 = 169
AC = 13m
So, Aman is 13 m away from his starting point.
Previous Year Questions 2020
Q13: All concentric circles are ___________ to each other. (2020) View Answer
View AnswerAns: All concentric circles arc similar to each other.
Q14: In figure, PQ || BC, PQ = 3 cm, BC = 9 cm and AC = 7.5 cm. Find the length of AQ. (2020)
 View Answer
View AnswerAns: Given, PQIIBC
PQ = 3 cm, BC = 9 cm and AC = 7.5 cm
Since. PQ || BC
∴ ∠APQ = ∠ABC (Corresponding angles are equal)
Now, in ΔAPQ and ΔABC
∠APQ =∠ABC (Corresponding angles are equal)
∠A = ∠A (Common)
ΔAPQ ∼ ΔABC (AA similarity)
Q15: In the given figure, EA/EC = EB/ED , prove that ΔEAB ~ ΔECD. (CBSE 2020)
 View Answer
View AnswerAns: In ΔEAB and ΔECD

Since, EA / EC = EB / ED
∠1 = ∠2 [Vertically opposite angles]
So, by SAS similarity rule ΔEAB ~ ΔECD
Hence, proved.
Previous Year Questions 2019
Q16: In the figure, GC||BD and GE||BF. If AC = 3cm and CD = 7 cm, then find the value of AE / AF. (2019)
 View Answer
View AnswerAns: 3/10
Here in the given figure.
GC || BD and GE || BF
AC = 3 cm and CD = 7 cm
By Basic Proportionality theorem.

We get, 

Q17: The perpendicular from A on the side BC of a ΔABC intersects BC at D, such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2. (2019)
 View Answer
View AnswerAns: We have, ΔABC such that AD⊥BC. ΔABC Intersect SC at D such that BD = 3CD.
In right ΔADB, by Pythagoras theorem, we have
AB2 = AD2 + BD2 _(i)
Similarly in ΔACD, we have AC2 = AD2 +CD2 _(ii)
Subtracting (ii) from (i), we get
AB2 - AC2 = BD2 - CD2 _(iii)
Now, BC = DB + CD = 4CD [∵ BD = 3CD]

Substituting the value of BD and CD in eqn.(iii) we get
Hence proved.
|
126 videos|457 docs|75 tests
|
FAQs on Previous Year Questions: Triangles - Mathematics (Maths) Class 10
| 1. What are the properties of triangles that I should know for Grade 10? |  |
| 2. How do I find the area of a triangle? |  |
| 3. What is the difference between an acute, obtuse, and right triangle? |  |
| 4. How can I determine if three lengths can form a triangle? |  |
| 5. What are some common triangle-related formulas I should memorize for exams? |  |

|
Explore Courses for Class 10 exam
|

|


















