JEE Main Previous year questions (2016-20): Matrices and Determinants | JEE Foundation - Class 9

Q.1. If the system of linear equations
2x + 2ay + az = 0
2x + 3by + bz = 0
2x + 4cy + cz = 0,
where a,b,c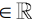are non-zero and distinct; has a non-zero solution, then    (2020)
(1) 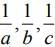 are in A.P.
(2) a, b, c are in G.P.
(3) a + b + c = 0
(4) a, b, c are in A.P.
Ans. (1) The system of linear equations is
2x + 2ay + az = 0     (1)
2x + 3by + bz = 0    (2)
2x + 4cy + cz = 0     (3)
The system of linear equations has a non- zero solution, then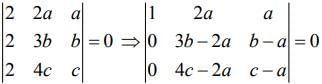

(R₂ → R₂ - R₁ and R₃ → R₃ - R₁)
⇒ (3b - 2a) (c -a) - (b-a) (4c - 2a) = 0
⇒
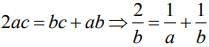
Hence, are in A.P.

Q.2. Let A = [a_ij] and B = [b_ij] be two 3 × 3 real matrices such that b_ij = (3)^{(i + j - 2)} a_ij, where i, j = 1, 2, 3. If the determinant of B is 81, then the determinant of A is    (2020)
(1) 1/3
(2) 1
(3) 1/81
(4) 1/9
Ans. (4)
We have b_ij = (3)^{(i + j - 2)}a_ij
Now,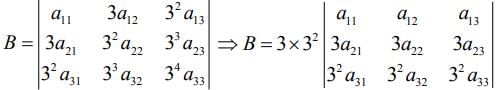




Q.3. If the system of linear equations,
x + y + z = 6
x + 2y + 3z = 10
3x + 2y + λz = μ
has more than two solutions, then μ - λ² is  equal to________.    (2020)
Ans. (13.00)
The system of linear equations is
x + y + z = 6    (1)
x + 2y + 3z = 10    (2)
3x + 2y + λz = μ    (3)
The system of equations has more than two solutions, then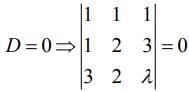

⇒1(2λ - 6) - 1 (λ - 9) + 1(2 - 6) = 0
⇒ 2λ - 6 - 1 λ - 9 - 4 = 0 ⇒ λ = 1
Now,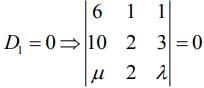

⇒ 6(2 - 3) - 1(10 - 3μ) + 1(20 - 20μ) = 0
⇒ -6 -10 + 3μ + 20 -2μ = 0 ⇒ μ = 14
Hence, μ - λ² =14 - 1 = 13

Q.4. For which of the following ordered pairs (μ, δ), the system of linear equations
x + 2y + 3z = 1
3x + 4y + 5z = μ
4x + 4y + 4z = δ
is inconsistent?    (2020)
(1) (4, 3)
(2) (4, 6)
(3) (1, 0)
(4) (3, 4)
Ans. (1)
The system of linear equation is
x + 2y + 3z = 1    (1)
3x + 4y + 5z = μ    (2)
4x + 4y + 4z = δ    (3)
On solving Eqs. (1), (2) and (3), we get
2(3x + 4y + 5z) - 2 (x + 2y + 3z) - 4x + 4y + 4z = 2μ - 2 - δ
⇒ 2μ - 2 - δ = 0 ⇒ δ = 2 (μ - 1)
From the given options only option (4,3) does not satisfies the above equation. So, the system of linear equations is inconsistent for the pair (4,3).

Q.5. If A =and I = 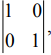then 10A⁻¹ is equal to    (2020)
(1) A – 4I
(2) 6I – A
(3) A – 6I
(4) 4I – A
Ans. (3)
Given,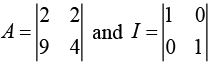
 
Now,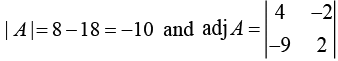
Therefore,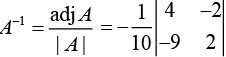



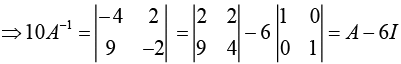
Q.6. The system of linear equations    (2020)
λx + 2y + 2z = 5
2λx + 3y + 5z = 8
4x + λy + 6z = 10 has
(1) no solution when λ = 8
(2) a unique solution when λ = -8
(3) no solution when λ = 2
(4) infinitely many solutions when λ = 2
Ans. (3)
The system of linear equations is
λx + 2y + 2z = 5    (1)
2λx + 3y + 5z = 8    (2)
4x + λy + 6z = 10    (3)
Therefore,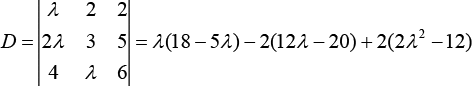

= λ² + 6λ + 16 = (λ + 8) (2 - λ)
For no solution, D = 0 ⇒ λ = 2.
Now,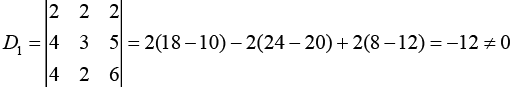

Hence, the system of linear equations has no solution for λ = 2.

Q.7. If the matrices A = 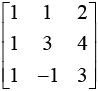, B = adj A and C = 3A, then 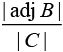is equal to    (2020)
(1) 8
(2) 16
(3) 72
(4) 2
Ans. (1)
From the properties of determinants of a square matrix of order n, we have
    (1)
Now,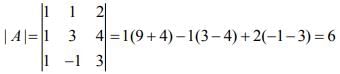

Hence, from Eq. (1), we get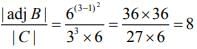


Q.8. The following system of linear equations    (2020)
7x + 6y - 2z = 0
3x + 4y + 2z = 0
x - 2y - 6z = 0, has
(1) Infinitely many solutions, (x, y, z) satisfying y = 2z.
(2) no solution.
(3) infinitely many solutions, (x, y, z) satisfying x = 2z.
(4) only the trivial solution.
Ans. (3)
The system of linear equation is
7x + 6y - 2z = 0    (1)
3x + 4y + 2z = 0    (2)
x - 2y - 6z = 0    (3)
Therefore, the coefficient matrix is given by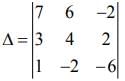

= 7(-24 + 4) -6(-18-2) -2(-6-4)
= -140 + 120 + 20 = 0
Also, Δ₁ = 0, Δ₂ = 0 and Δ₃ = 0
Hence, for the given system of equation infinite many solutions are possible.
From Eqs. (1) and (3), we get
7x + 6y - 2z + 3(x - 2y - 6z) = 0 ⇒ x = 2z

Q.9. Let a – 2b + c = 1. If f(x) =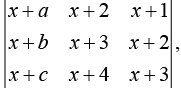then    (2020)
(1) f (−50)= 501
(2) f (−50) = − 1
(3) f (50) = - 501
(4) f (50) = 1
Ans. (4)
Given,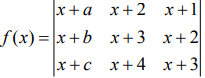

R₁→R₁ + R₃ - 2R₂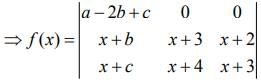


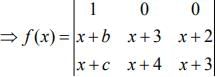
⇒ f (x) = {(x+3)² - (x+2)(x+4)}
= x² +9 + 6x - x² - 6x - 8 = 1
Hence, f (50) = 1

Q.10. Let α be a root of the equation 2x² + x + 1 = 0 and the matrix 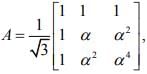then the matrix A³¹ is equal to    (2020)
(1) A
(2) I³
(3) A²
(4) A³
Ans. Given α be a root of the equation x² + x + 1 = 0
α = ω , ω²
Now,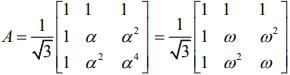




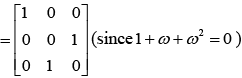
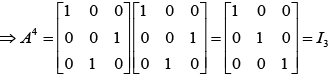
Hence, A³¹ = A²⁸ . A³ = A³

Q.11. The number of all 3 × 3 matrices A, with entries from the set {−1, 0, 1} such that the sum of the diagonal elements of AA^T is 3, is ________.    (2020)
Ans. (672.00)
The trace of matrix  AA^T is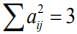

Hence, the number of such matrices is
⁹C₃ x 2³ = 84 x 8 = 672

Q.12. The system of linear equations     (2019)
x + y + z = 2
2x + 3y + 2z = 5
2x + 3y + (a² - 1)z = a + 1
(1)  is inconsistent when a = 4
(2) has a unique solution for |a| = √3
(3) has infinitely many solutions for a = 4
(4) is inconsistent when |a| = √3
Ans. (4)
Solution. Since the system of linear equations are
x+y + z = 2    ...(1)
2x + 3y + 2z = 5    ...(2)
2x + 3y + (a² - 1) z = a + 1    ...(3)
Now,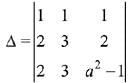
⇒
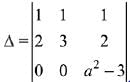
(Applying R₃ → R₃ - R₂)
= a² - 3
When, A = 0 ⇒ a² - 3 = 0 ⇒ |a|= √3
If a² = 3, then plane represented by eqn (2) and eqn (3) are parallel.
Hence, the given system of equations is inconsistent.

Q.13. then the matrix A^-50 when θ = π/12, is equal to:    (2019)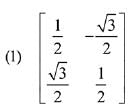




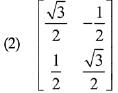
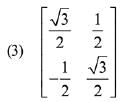
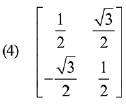
Ans. (3)
Solution.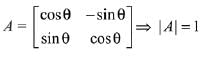








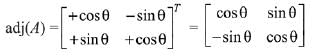
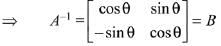
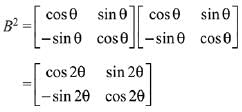
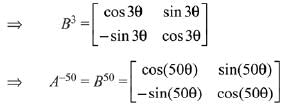
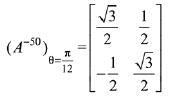
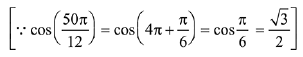
Q.14. If the system of linear equations      (2019)
x - 4y + 7z = g
3y - 5z = h
- 2x + 5y - 9z = k
is consistent, then:
(1) g + 2h + k = 0
(2) g + h + 2k = 0
(3) 2g + h + k = 0
(4) g + h + k = 0
Ans. (3)
Solution.
Consider the system of linear equations
x - 4y + 7z = g    ...(i)
3y - 5z = h    ... (ii)
-2x + 5y - 9z = k    ...(iii)
Multiply equation (i) by 2 and add equation (i), equation (ii) and equation (iii)
⇒  0 = 2g + h + k.  ∴ 2g + h + k = 0
then system of equations is consistent.

Q.15. If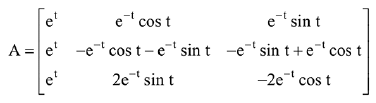
then A is:     (2019)
(1) invertible for all t ∈ R.
(2) invertible only if t = π.
(3) not invertible for any t ∈ R.
(4) invertible only if t = π/2.
Ans. (1)
Solution.




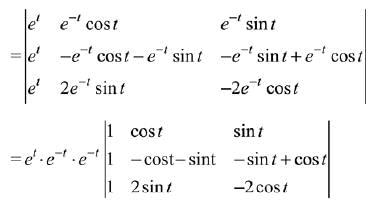
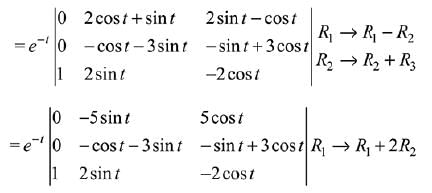
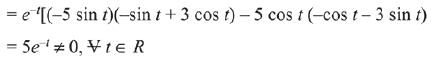
∴ A is invertible.

Q.16. If the system of equations      (2019)
x + y + z = 5
x + 2y + 3z = 9
x + 3y + αz = β
has infinitely many solutions, then β - α equals:
(1) 21
(2) 8
(3) 18
(4) 5
Ans. (2)
Solution.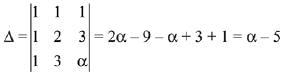





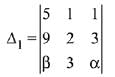
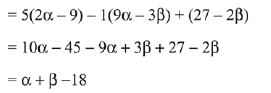
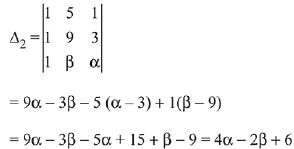
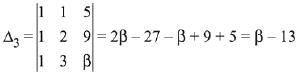
Since, the system of equations has infinite many solutions. Hence,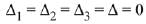



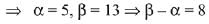
Q.17. The number of values of θ ∈ (0, π) for which the system of linear equations       (2019)
x + 3y + 7z = 0
- x + 4y + 7z = 0
(sin 3θ)x + (cos 2θ)y + 2z = 0
has a non-trivial solution, is:
(1) three
(2) two
(3) four 
(4) one
Ans. (2)
Solution.
Since, the system of linear equations has non-trivial solution then determinant of coefficient matrix = 0

sin3θ(21 - 28) - cos2θ(7 + 7) + 2 (4 + 3) = 0
sin3θ + 2cos2θ - 2 = 0
3sinθ - 4sin³θ + 2 - 4sin²θ - 2 = 0
4sin³θ + 4sin²θ - 3sinθ = 0
sinθ (4sin²θ + 4sinθ - 3) = 0
sinθ (4sin²θ + 6sinθ - 2sinθ - 3) = 0
sinθ [2sinθ (2sinθ - 1) + 3 (2sinθ - 1)] = 0
sinθ (2sinθ - 1) (2sinθ + 3) = 0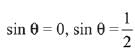
 

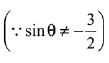
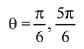
Hence, for two values of θ, system of equations has non-trivial solution.

Q.18. 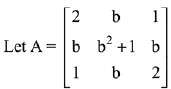 where b > 0. Then the minimum value of  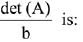    (2019)
(1) 2√3
(2) -2√3
(3) -√3
(4) √3
Ans. (1)
Solution.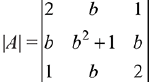

= 2(2b² + 2 - b²)- b(2b - b)+ 1 (b² - b² - 1)
= 2b² + 4 - b² - 1 = b² + 3

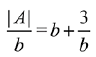
Using A.M≥G.M,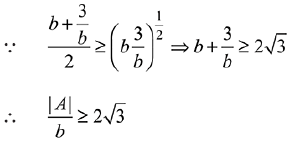



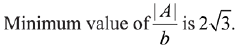
Q.19. If the system of linear equations       (2019)
2x + 2y + 3z = a
3x - y + 5z = b
x - 3y + 2z = c
where, a, b, c are non-zero real numbers, has more than one solution, then:
(1) b - c + a = 0
(2) b - c - a = 0
(3) a + b + c = 0
(4) b + c- a = 0
Ans. (2)
Solution.
∵ System of equations has more than one solution
∴ Δ = Δ₁ = Δ₂ = Δ₃ = 0 for infinite solution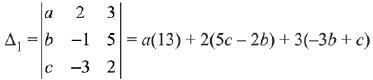



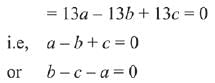
Q.20.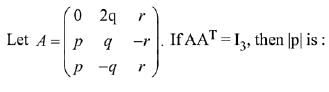 

(1) 1/√5
(2) 1/√3
(3) 1/√2
(4) 1/√6
Ans. (3)
Solution.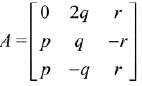






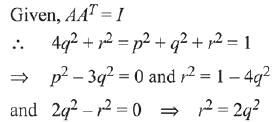
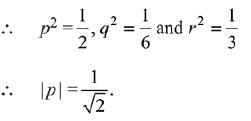
Q.21.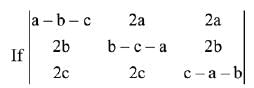 

= (a + b + c) (x + a + b + c)², x ≠ 0 and a + b + c ≠ 0, then x is equal to:     (2019)
(1) abc
(2) -(a + b + c)
(3) 2(a + b + c)
(4) -2(a + b + c)
Ans. (4)
Solution.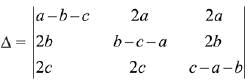






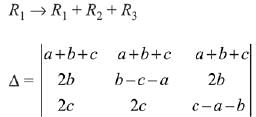
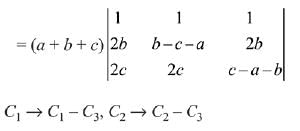
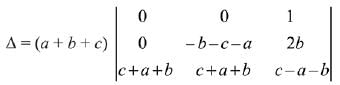
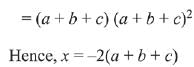
Q.22. Let A and B be two invertible matrices of order 3 x 3. If det (ABA^T) = 8 and det (AB^-1) = 8, then det (BA^-1 B^T) is equal to:     (2019)
(1) 1/4
(2) 1
(3) 1/16
(4) 16
Ans. (3)
Solution.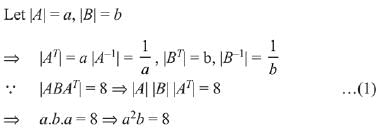




Q.23. An ordered pair (α, β) for which the system of linear equations
(1 + α)x + βy + z = 2
ax + (1 + β)y + z = 3
αx+ βy+ 2z = 2
has a unique solution, is :     (2019)
(1) (2, 4)
(2) (-3, 1)
(3) (-4, 2)
(4) (1, -3)
Ans. (1)
Solution.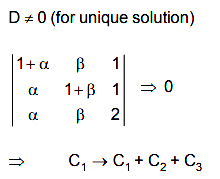



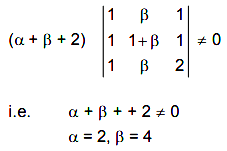
Q.24.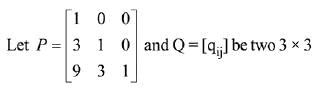  
 matrices such that Q - P⁵ = I₃. Then 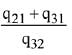is equal to:     (2019)
(1) 10
(2) 135
(3) 15
(4) 9
Ans. (1)
Solution.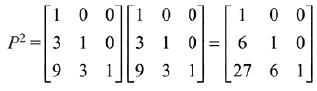






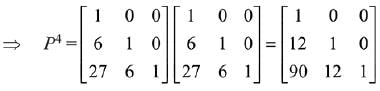
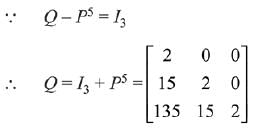
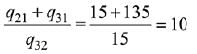
Q.25.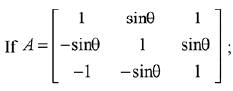 
 then for all  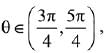det (A) lies in the interval:     (2019)




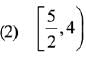
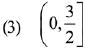
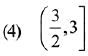
Ans. (4)
Solution.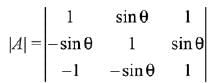







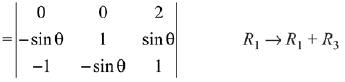
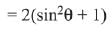
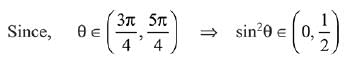
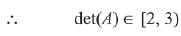
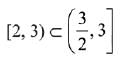
Q.26. The set of all values of λ for which the system of linear equations     (2019)
x - 2y - 2z = λx
x + 2y + z = λy
- x - y = λ2
has a non-trivial solution:
(1) is a singleton
(2) contains exactly two elements
(3) is an empty set
(4) contains more than two elements
Ans. (1)
Solution.
Consider the given system of linear equations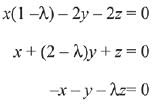

Now, for a non-trivial solution, the determinant of coefficient matrix is zero.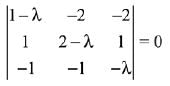

⇒ (1 - λ)³ = 0
λ = 1

Q.27. The greatest value of c ∈ R for which the system of linear equations     (2019)
x - cy - cz = 0
cx - y + cz = 0
cx + cy - z = 0
has a non-trivial solution, is:
(1) -1
(2) 1/2
(3) 2
(4) 0
Ans. (2)
Solution.
If the system of equations has non-trivial solutions, then the determinant of coefficient matrix is zero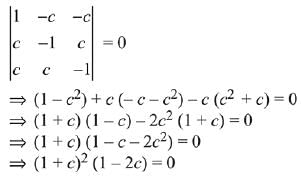


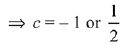
Hence, the greatest value of c is 1/2 for which the system of linear equations has non-trivial solution.

Q.28.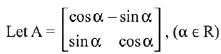 , (α ∈ R) such that .
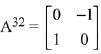Then a value of α is:     (2019)
(1) π/32
(2) 0
(3) π/64
(4) π/16
Ans. (3)
Solution.





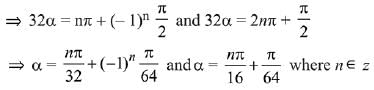
Q.29. Let the numbers 2, b, c be in an A.P. and 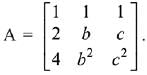 , If det(A)∈ [2, 16], then c lies in the interval:     (2019)
(1) [2,3)
(2) (2 + 2^3/4, 4)
(3) [4,6]
(4) [3,2 + 2^3/4]
Ans. (3)
Solution.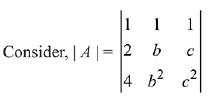




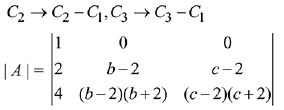
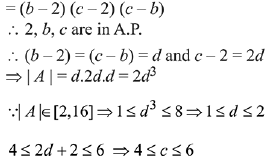
Q.30. If the system of linear equations
x - 2y + kz = 1
2x + y + z = 2
3x - y - kz = 3
has a solution (x, y, z), z = ≠ 0, then (x, y) lies on the straight line whose equation is:     (2019)
(1) 3x - 4y - 1 = 0
(2) 4x - 3y - 4 = 0
(3) 4x - 3y - 1 = 0
(4) 3x - 4y - 4 = 0
Ans. (2)
Solution.
Given system of linear equations,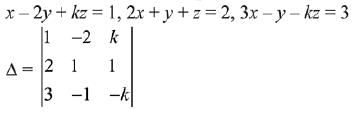




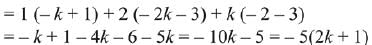
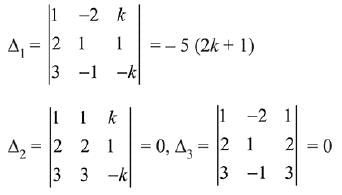
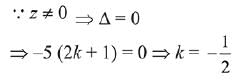
∴ System of equation has infinite many solutions.


Q.31.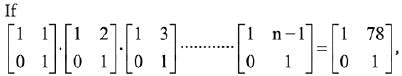
 then the inverse of  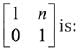    (2019)




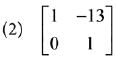
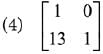
Ans. (2)
Solution.



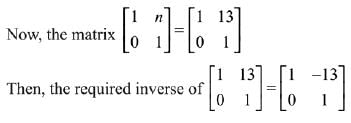
Q.32. Let α and β be the roots of the equation x² + x + 1 = 0. Then for y ≠ 0 in R,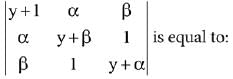
      (2019)
(1) y(y² - 1)
(2) y(y² - 3)
(3) y³
(4) y³ - 1
Ans. (3)
Solution.
Let α = ω and β = ω² are roots of x² + x + 1 = 0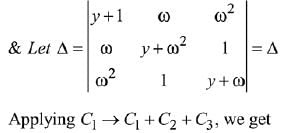






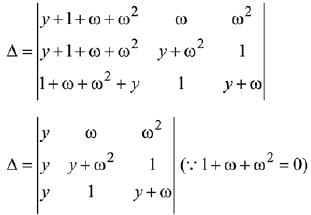
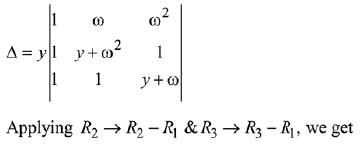
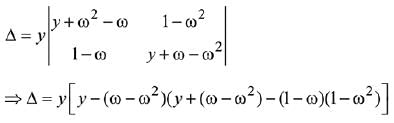
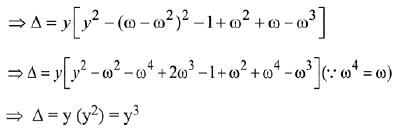
Q.33. The total number of matrices 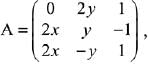 (x, y ∈ R, x ≠ y) for which A^TA = 3I₃ is:     (2019)
(1) 2
(2) 3
(3) 6
(4) 4
Ans. (4)
Solution.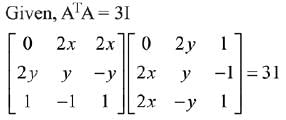

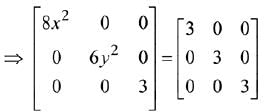
Number of combinations of (x, y) = 2 x 2 = 4

Q.34. If the system of equations 2x + 3y - z = 0, x + ky - 2z - 0 and 2x - y + z = 0 has a non-trivial solution (x, y, z), then 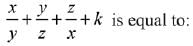     (2019)
(1) 3/4
(2) 1/2

(4) -4
Ans. (2)
Solution.
Given system of equations has a non-trivial solution.

∴ equations are 2x + 3y - z = 0    ...(i)
2x - y + z = 0    ... (ii)
2x + 9y - 4z = 0    ...(iii)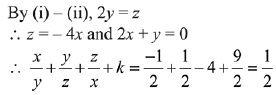


Q.35.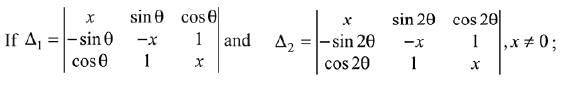  

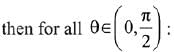       (2019)
(1) Δ₁ - Δ₂ = -2x³
(2) Δ₁ - Δ₂ = x(cos2θ - cos4θ)
(3) Δ₁ x Δ₂ = -2(x³ + x - 1)
(4) Δ₁ + Δ₂ = -2x³ 
Ans. (4)
Solution.

= x (- x² - 1) - sin θ (- x sin θ - cos θ)+ cos θ (- sin θ + x cos θ)
= - x³ - x + x sin²θ + sin θ cos θ - cos θ sin θ + x cos²θ
= -x³ - x + x = -x³
Similarly, Δ₂ = - x³   Then, Δ₁ + Δ₂ = - 2x³

Q.36. If the system of linear equations
x + y + z = 5
x + 2y + 2z = 6
x + 3y + λz = μ, (λ, μ ∈ R), has infinitely many solutions, then the value of λ + μ is :       (2019)
(1) 12
(2) 9
(3) 7 
(4) 10
Ans. (4)
Solution.
Given system of linear equations: x + y + z = 5; x + 2y + 2z = 6 and x + 3y + λz = μ have infinite solution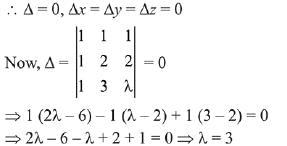



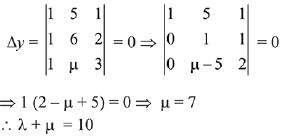
Q.37. Let λ be a real number for which the system of linear equations:
x + y + z = 6
4x + λy - λz = λ -2
3x + 2y - 4z = -5
has infinitely many solutions. Then λ is a root of the quadratic equation:      (2019)
(1) λ² + 3λ - 4 = 0
(2) λ² - 3λ - 4 = 0
(3) λ² + λ - 6 = 0
(4) λ² - λ - 6 = 0
Ans. (4)
Solution. ∵ system of equations has infinitely many solutions.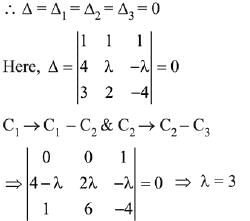


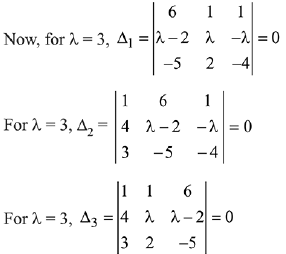
∴ for λ = 3, system of equations has infinitely many solutions.

Q.38. The sum of the real roots of the equation       (2019)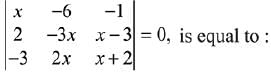

(1) 6
(2) 0
(3) 1
(4) -4
Ans. (2)
Solution.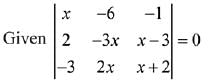

On expanding,
x (- 3x² - 6x - 2x² + 6x) - 6 (- 3x + 9 - 2x - 4) - (4x - 9x) = 0
⇒ x (- 5x²) - 6 (- 5x + 5) - 4x + 9x = 0
⇒ x³ - 7x + 6 = 0
∵ all the roots are real.
∴ sum of real roots = 0/1 = 0

Q.39. If A is a symmetric matrix and B is a skew-symmetrix matrix such that 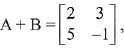then AB is equal to:      (2019)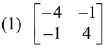




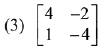
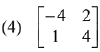
Ans. (2)
Solution.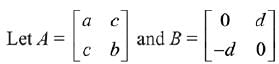


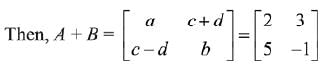
On comparing each term,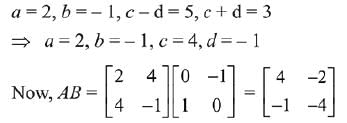


Q.40. If  is the inverse of a 3 x 3 matrix A, then the sum of all values of α for which delta (A) + 1 = 0, is:       (2019)
(1) 0
(2) -1
(3) 1 
(4) 2
Ans. (3)
Solution.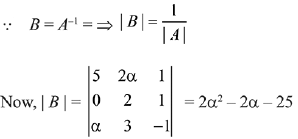



Q.41. If 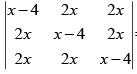 = ( A + Bx)( x- A)2 , then the ordered pair (A, B) is equal to:     (2018)
(1) (-4, -5)
(2) (-4, 3)
(3) (-4, 5)
(4) (4, 5)
Ans. (3)
Solution.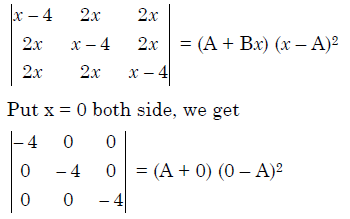







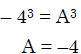
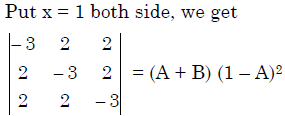
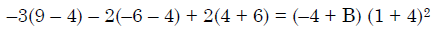
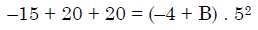
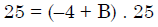
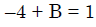
B = 5

Q.42. If the system of linear equations
x + ky + 3z = 0
3x + ky - 2z = 0
2x + 4y - 3z = 0
has a non-zero solution (x, y, z), then xz/y² is equal to:    (2018)
(1) -10
(2) 10
(3) -30
(4) 30
Ans: (2)
Solution.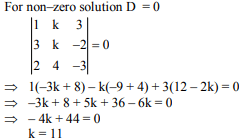

hence equations are x + 11y + 3z = 0
3x + 11y - 2z = 0
and 2x + 4y - 3z = 0
let z = t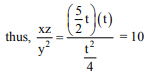


Q.43. Let S be the set of all real values of k for which the system of linear equations      (2018)
x+ y + z = 2
2x + y - z = 3
3x + 2y + kz = 4
has a unique solution.  
Then S is :
(1) S equal to {0}
(2) equal to R-{0}
(3) an empty set
(4) equal to R
Ans. (2)
Solution.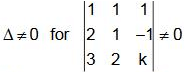



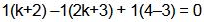
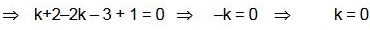
Therefore, set S = equal to R-{0}

Q.44. Let A be a matrix such that A ∙ 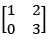 is a scalar matrix and |3A| = 108. Then A² equals:     (2018)
(1)
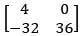
(2)
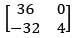
(3)
(4)
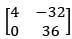
Ans: (3)
Solution: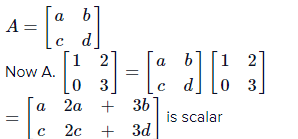

∴ c = 0, 2a + 3b = 0, a = 2c + 3d  a = 3d
∴a² = 9d² = 36
|3A| = 108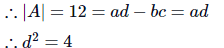


Hence, option 3 is the answer.

Q.45. Let A = and B = A²⁰. Then the sum of the elements of the first column of B is:     (2018)
(1) 210
(2) 211
(3) 251
(4) 231
Ans: (4)
Solution: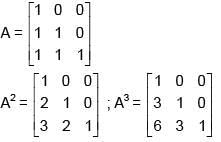


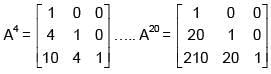
Sum of the elements of first column = 231

Q.46. If S is the set of distinct values of b for which the following system of linear equations    (2017)
x +y+ z = 1
x +ay+ z = 1
ax + by+ z = 0
has no solution, then S is
(1) A singleton
(2) An empty set
(3) An infinite set
(4) A finite set containing two or more elements
Ans. (1)
Solution: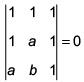
⇒ –(1 – a)2 = 0
⇒ a = 1
For a = 1
Eq. (1) & (2) are identical i.e.,x + y + z = 1
To have no solution with x + by + z = 0
b = 1

Q.47.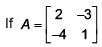,then adj (3A² + 12A) is equal to     (2017)
(1)
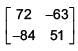
(2)
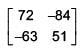
(3)
(4)
Ans. (3)
Solution.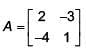

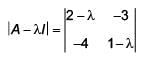
= (2 – 2λ- λ + λ²) - 12
f (λ)= λ² - 3λ - 10
∵ A satisfies f (λ)
∴ A² – 3A –10I = 0
A² – 3A = 10I
3A² – 9A = 30I
3A² + 12A = 30I + 21A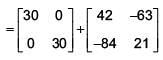




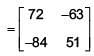
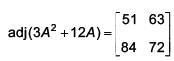
Q.48. The number of real values of λ for which the system of linear equations
2x + 4y – λz = 0
4x + λy + 2z = 0
λx + 2y + 2z = 0
has infinitely many solutions, is:    (2017)
(1) 3
(2) 1
(3) 2
(4) 0
Ans. (2)
Solution.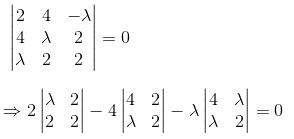


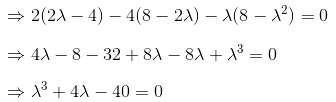
It will give only one real value of λ

Q.49. For two 3 × 3 matrices A and B, let A+B = 2B' and 3A + 2B = I₃, where B' is the transpose of B and I₃ is 3×3 identity matrix. Then:     (2017)
(1) 10A + 5B = 3I₃
(2) 3A + 6B = 2I₃
(3) 5A + 10B = 2I₃
(4) B + 2A = I₃
Ans. (1)
Solution.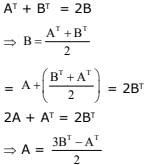

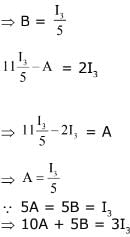
Q.50. If A = 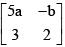 and A adj A = A A^T, then 5a + b is equal to:    (2016)
(1) -1
(2) 5
(3) 4
(4) 13
Ans. (2)

Equate,  10a + 3b = 25a² + b²
& 10a + 3b = 13
& 15a - 2b = 0
a/2 = b/15 = k (let) 
Solving a = 2/5, b = 3 
So, 5a + b = 5 x 2/5 + 3 = 5 

Q.51. The system of linear equations
x + λy - z = 0
λx - y - z = 0
x + y - λz = 0
has a non-trivial solution for:    (2016)
(1) infinitely many values of λ
(2) exactly one value of λ
(3) exactly two values of λ
(4) exactly three values of  λ
Ans. (4)
For trivial solution,

 

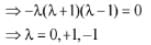
Q.52. The number of distinct real roots of the equation, 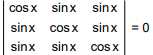 in the interval  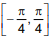is:    (2016)
(1) 4
(2) 1
(3) 2
(4) 3
Ans. (3)
Solution.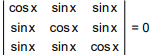


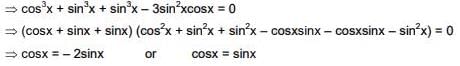
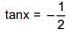   tanx = 1 ⇒ x = π/4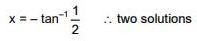


Q.53. If P =  then P^T Q²⁰¹⁵ P is    (2016)
(1)
(2)
(3)
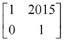
(4)
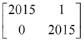
Ans. (3)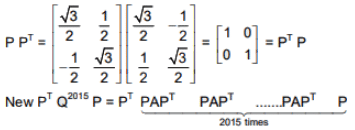


⇒ Aⁿ = nA - (n-1)I
⇒

Q.54. Let A be a 3 × 3 matrix such that A² - 5A + 7I = 0.
Statement - I: A^-1 = 1/7(5I-A).
Statement - II : The polynomial A³ - 2A² - 3A + I can be reduced to 5(A - 4I).
Then    (2016)
(1) Statement-I is false, but Statement-II is true.
(2) Both the statements are false.
(3) Both the statements are true.
(4) Statement-I is true, but Statement-II is false.
Ans. (3)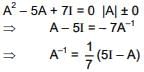

Hence, statement 1 is true
Now A³ - 2A² - 3A + I = A(A²) - 2A² - 3A + I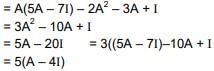

Statement 2 is also correct

Q.55. If A = 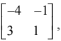  then the determinant of the matrix (A²⁰¹⁶ - 2A²⁰¹⁵ - A²⁰¹⁴) is    (2016)
(1) 2014
(2) 2016
(3) -175
(4) -25
Ans. (4)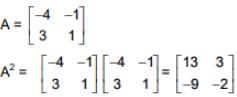


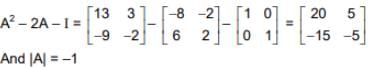
⇒ A²⁰¹⁶ - 2A²⁰¹⁵ - A²⁰¹⁴| = |A|²⁰¹⁴ |A² - 2A - I| = 1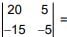  (-100 + 75) = -25