Probability and Statistics | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: In a sample of 100 heart partients, each patients has 80% chance of having a heart attack without medicine X. It clinically known that medicine X reduces the probability of having a heart attack by 50%. Medicine X is taken by 50 of these 100 patients. The probability that a randomly selected patient, out of the 100 patients, takes medicine X and has a heart attack is (2024 SET-2)
(a) 40%
(b) 60%
(c) 20%
(d) 30%
Ans: (c)
Sol: Probability of having a heart attack without medicine = 80%
Probability of having a heart attack with medicine = (80%) × 0.5 = 40%
Total probability that a randomly selected patient out of 100 takes medicines X and has a heart attack.
= (50/100) x 0.4 = 0.2 = 20%.
Q2: The probability that a student passes only in Mathematics is 1/3. The probability that the student passes only in English is 4/9. The probability that the student passes in both of these subjects is 1/6. The probability that the student will pass in at least one of these two subjects is (2024 SET-1)
(a) 17/18
(b) 11/18
(c) 14/18
(d) 1/18
Ans: (a)
Sol: 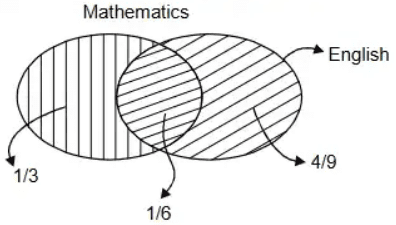 P(A ∪ B ∪ C) → Probability that the student passes is atleast one subject.
P(A ∪ B ∪ C) → Probability that the student passes is atleast one subject.
P(A ∪ B ∪ C) = 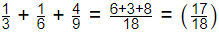
Q1: A remote village has exactly 1000 vehicles with sequential registration numbers starting from 1000 . Out of the total vehicles, 30% are without pollution clearance certificate. Further, even- and oddnumbered vehicles are operated on even- and oddnumbered dates, respectively.
If 100 vehicles are chosen at random on an evennumbered date, the number of vehicles expected without pollut
ion clearance certificate is.
(a) 15
(b) 30
(c) 50
(d) 70
Ans: (b)
Sol: Since 30% of the total vehicles are without pollution clearance certificate.
Out of the 100 chosen vehicle, 30% i.e. 100 × 0.3 = 30 vehicle are expected to be without pollution clearance certificate.
Q2: Which of the following probability distribution functions (PDFs) has the mean greater than the median? (2023 SET-2)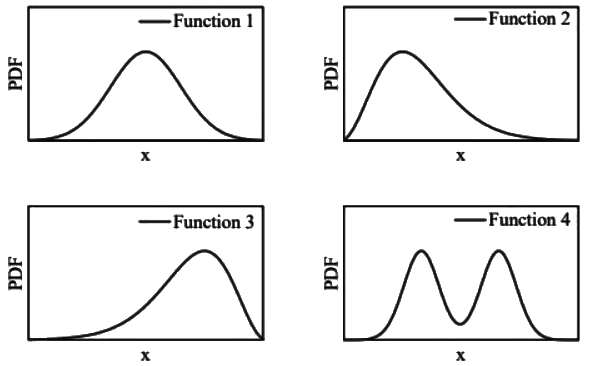 (a) Function 1
(a) Function 1
(b) Function 2
(c) Function 3
(d) Function 4
Ans: (b)
Sol: 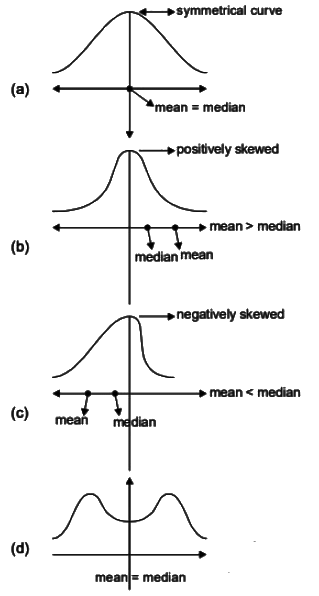 Option (B) is correct.
Option (B) is correct.
Q3: The probabilities of occurrences of two independent events A and B are 0.5 and 0.8, respectively. What is the probability of occurrence of at least A or B (rounded off to one decimal place)? (2023 SET-1)
Ans: 0.9 to 0.9
Sol: P(A) = 0.5
P(B) = 0.8
Probability of occurence of atleast A or B = P(A ∩ B)
P(A ∩ B) = P(A) + P(B) − P(A ∩ B)
= 0.5 + 0.8 − P(A) × P(B)
= 0.5 + 0.8 − 0.5 × 0.8
= 1.3 − 0.4
= 0.9
Q1: A pair of six-faced dice is rolled thrice. The probability that the sum of the outcomes in each roll equals 4 in exactly two of the three attempts is ______. (round off to three decimal places) (2022 SET-2)
Ans: 0.018 to 0.02
Sol: Event, E = {(1, 3)(3, 1)(2, 2)}
n(E) = 3
n(S) = 36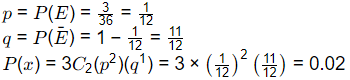
Q2: Match the following attributes of a city with the appropriate scale of measurements.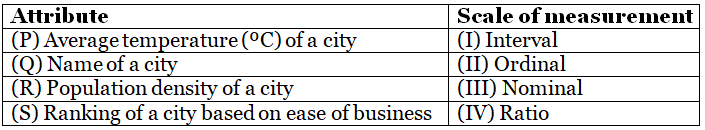 Which one of the following combinations is correct? (2022 SET-2)
Which one of the following combinations is correct? (2022 SET-2)
(a) (P)-(I), (Q)-(III), (R)-(IV), (S)-(II)
(b) (P)-(II), (Q)-(I), (R)-(IV), (S)-(III)
(c) (P)-(II), (Q)-(III), (R)-(IV), (S)-(I)
(d) (P)-(I), (Q)-(II), (R)-(III), (S)-(IV)
Ans: (a)
Sol: Meaning of
Nominal → a name or term
Ordinal → in an ordered sequence
Ratio → quantitative relation between two things
Interval → indicates average of a range
Q3: A set of observations of independent variable (x) and the corresponding dependent variable (y) is given below.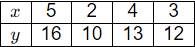
Based on the data, the coefficient a of the linear regression model y = a + bx is estimated as 6.1.
The coefficient b is ______________ . (round off to one decimal place) (2022 SET-1)
Ans: 1.9 to 1.9
Sol: We know that, normal equation for fitting of straight lines are
Σy = na + bΣx
Σxy = aΣx + bΣx2
n = 4
51 = 4a + b(14)
188 = a(14) + b(54)
After solving, a = 6.1 and b = 1.9
Q1: The shape of the cumulative distribution function of Gaussian distribution is (2021 SET-1)
(a) Horizontal line
(b) Straight line at 45 degree angle
(c) Bell-shaped
(d) S-shaped
Ans: (d)
Sol: 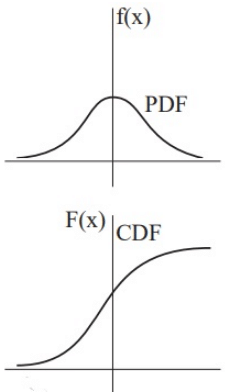
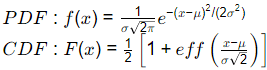
Q1: A fair (unbiased) coin is tossed 15 times. The probability of getting exactly 8 Heads (round off to three decimal places), is ________. (2020 SET-2)
Ans: 1.19 to 1.2
Sol: P(H) = 1/2
P(T) = 1/2
Probability of getting exactly 8 heads out of 15 trial = 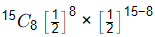 = 0.196
= 0.196
Q1: The probability density function of a continuous random variable distributed uniformly between x and y (for y > x) is [2019 : 2 Marks, Set-II]
(a) y - x
(b) 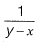
(c) ) x - y
(d) 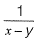
Ans: (b)
Sol: Probability density function of uniform distribution is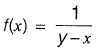
Q1: Probability (up to one decimal place) of consecutively picking 3 red balls without replacement from a box containing 5 red balls and 1 white ball is _______ . [2018 : 1 Mark, Set-II]
Ans: (0.5)
Sol: Probability 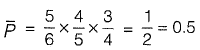
Q2: The graph of a funotion f{x) is shown in the figure

For f(x) to be valid probability density function, the value of h is [2018 : 1 Mark, Set-II]
(a) 1/3
(b) 2/3
(c) 1
(d) 3
Ans: (a)
Sol:
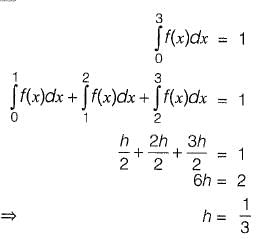
Q3: A probability distribution with right skew is shown in the figure.

The correct statement for the probability distribution is
(a) Mean is equal to mode
(b) Mean is greater than median but less than mode
(c) Mean is greater than median and mode
(d) Mode is greater than median. [2018 :1 Mark, Set-II]
Ans: (c)
Sol:
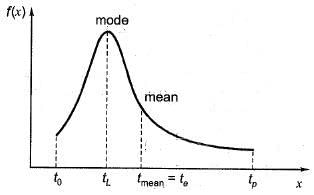
tL < fmea = Curve is skew to right,
mode < mean
i.e., mean > median and mode
Mean is greater than the mode and the median. This is common for a distribution that is skewed, to the right [i.e., bunched up toward the left and a ‘tail’ stretching toward the right].
Q1: For the function f(x) = a + bx, 0 ≤ x ≤ 1, to be a valid probability density function, which one of the following statements is correct? [2017 : 2 Marks, Set-I]
(a) a = 1, b = 4
(b) a = 0.5, b = 1
(c) a = 0, b = 1
(d)a = 1, b = 1
Ans: (b)
Sol:

Q2: The number of parameters in the univariate exponential and Gaussian distributions, respectively, are [2017 : 1 Mark, Set-I]
(a) 2 and 2
(b) 1 and 2
(c) 2 and 1
(d) 1 and 1
Ans: (b)
Sol: In exponential,
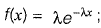 x = 0
x = 0
The parameter is λ.
In Gaussin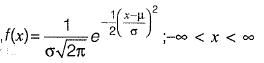
The parameters are µ and α.
Therefore, answer is (b).
Q3: If f(x) arid y(x) are two probability density functions,
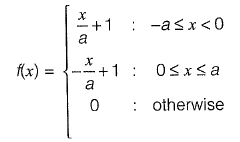

Which one of the following statements is true? [2017 : 1 Mark, Set-I]
(a) Mean of f(x) and g(x) are same; Variance of f{x) and g(x) are same
(b) Mean of f(x) and g(x) are same; Variance of f(x) and g(x) are different
(c) Mean of f(x) and g(x) are different; Variance of f(x) and g(x) are same
(d) Mean of f(x) and g(x) are different; Variance of f(x) and g(x) are different
Ans: (b)
Sol: Mean of f(x) is t(x)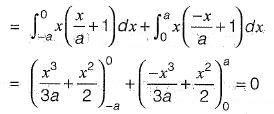
Variance of f(x) is E(x)2 - {E(x)2} where
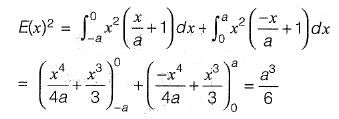
⇒ Variance is a3/6
Next, mean of g(x) is E(x)
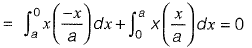
Variance of g(x) is E(x2) - {E(x)}2, where,

⇒ Variance is a3/2
∴ Mean of f(x) and g(x) are same but variance of f(x) and g(x) are different
Q1: X and T are two random independent events. It is known that P (X ) = 0.40 and P { X ∪ Yc ) = 0.7. Which one of the following is the value of P (X ∪ Y)? [2016 : 1 Mark, Set-II]
(a) 0.7
(b) 0.5
(c) 0.4
(d) 0.3
Ans: (a)
Sol:
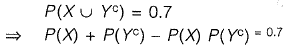
(Since X, Y are independent events)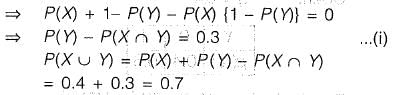
Q2: Probability density function of a random variable X is given below
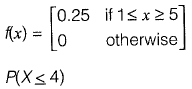 [2016 : 2 Marks, Set-I]
[2016 : 2 Marks, Set-I]
(a) 3/4
(b) 1/4
(c) 1/4
(d) 1/8
Ans: (a)S
Sol:
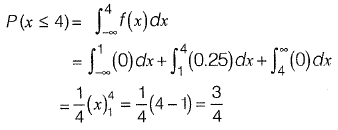
Q1: The probability density function of a random variable, x is
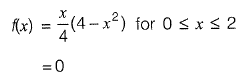
The mean, μx of the random variable is________ [2015 : 2 Marks, Set-11]
Ans: 1.066
Sol:
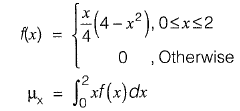
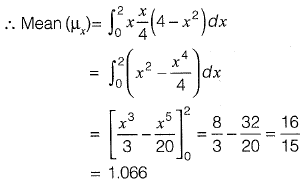
Q2: Consider the following probability mass function (p.m.f.) of a random variable X.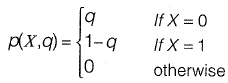
if q = 0.4, the variance of X is __________
Ans: 0.24
Sol: Given

Required value = V(X) = E{X2) - [E{X)]2
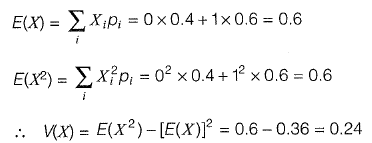
Q1: A traffic office im poses on an average 5 number of penalties daily on traffic violators. Assume that the number of penalties on different days is independent and follows a Poisson distribution. The probability that there will be less than 4 penalties in a day is __________ . [2014 : 2 Marks, Set-I
Ans: 0.265
Sol: Mean λ, = 5
P(x < 4) = { p(x = 0) + p(x = 1) + p(x = 2) + p(x = 3)}
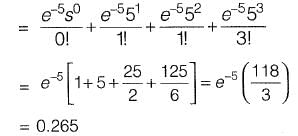
Q2: A fair (unbiased) coin was tossed four times in succession and resulted in the following outcomes: (i) Head, (ii) Head, (iii) Head, (iv) Head. The probability of obtaining a 'Tail' when the coin is tossed again is
(a) 0
(b) 1/2
(c) 4/5
(d) 1/5
Ans: b
Sol: 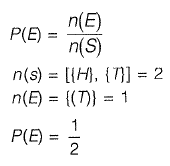
Q3: The probability density function of evaporation E on any day during a year in a watershed is given by
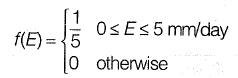
The probability that Elies in between 2 and 4 mm/day in a day in the watershed is (in decimal)_____ . [2014 : 1 Mark, Set-I]
Ans: 0.4
Sol:
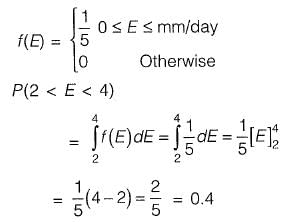
Q1: Find the value of λ such that function f(x) is valid probability density function f(x) = λ(x - 1) ( 2 - x) for 1 ≤ x ≤ 2 = 0 otherwise [2013 : 2 Marks]
Ans: 6
Sol:
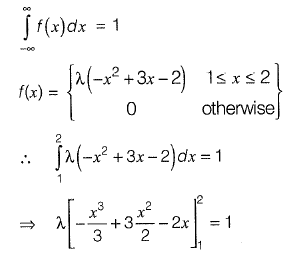
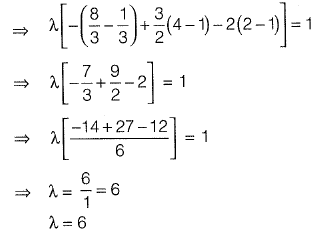
Q1: In an experiment, positive and negative values are equally likely to occur. The probability of obtaining at most one negative value in five trials is [2011 : 2 Marks]
(a) 1/32
(b) 2/32
(c) 3/32
(d) 6/32
Ans: d
Sol: Since negative and positive are equally likely, the distribution of number of negative values is binomial with n = 5 and p = 1/2
Let X represent number of negative values in 5 trials.
p(at most 1 negative value
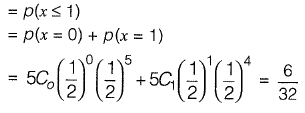
Q2: The annual precipitation data of a city is normally distributed with mean and standard deviation as 1000 mm and 200 mm, respectively. The probability that the annual precipitation will be more than 1200 mm is [2011 : 2 Marks]
(a) <50%
(b) 50%
(c) 75%
(d) 100%
Ans: a
Sol: The annual precipitation is normally distributed with μ = 1 000 mm and σ = 200 mm
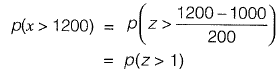
Where z is the standard normal variate.
In normal distribution Now, since p(-1 < z < 1) ≈ 0.68
(≈ 68% of data is within one standard deviation of mean)

Q3: There are two containers, with one containing 4 red and 3 green balls and the other containing 3 blue and 4 green balls. One ball is drawn at random from each container. The probability that one of the balls is red and the other is blue will be [2011 : 1 Mark]
(a) 1/7
(b) 9/49
(c) 12/49
(d) 3/7
Ans: c
Sol: p(one ball is Red & another is blue)
= p(first is Red and second is Blue)
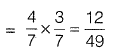
Q1: Two coins are simultaneously tossed. The probability of two heads sim ultaneously appearing is [2010 : 1 Mark]
(a) 1/8
(b) 1/6
(c) 1/4
(d) 1/2
Ans: c
Sol: 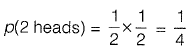
FAQs on Probability and Statistics - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What is the difference between probability and statistics? |  |
| 2. How do I calculate the mean, median, and mode of a dataset? |  |
| 3. What are the main types of probability? |  |
| 4. What is a normal distribution and why is it important? |  |
| 5. How can I determine if a dataset is normally distributed? |  |





















