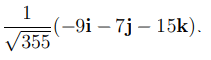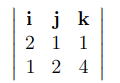Product of Vectors | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Product of Vectors |

|
| Dot Product (Scalar Product) |

|
| Cross Product (Vector Product) |

|
| Other Applications of Product of Vectors |

|
Product of Vectors
There are two types of ways we can combine vectors. Vectors have both size and direction.
- The first way is called the dot product, which is also known as the scalar product. When we do the dot product of two vectors, we get a single number, not another vector. This result is a scalar quantity.
- The second way is called the cross product, also known as the vector product. When we do the cross-product, we get a new vector that is perpendicular (at a right angle) to the original two vectors.
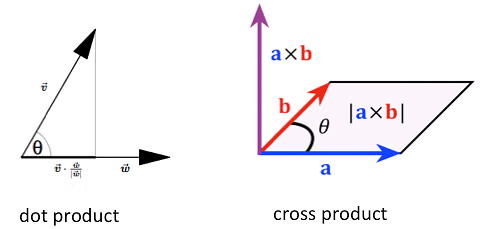 Vector Multiplication
Vector Multiplication
Dot Product (Scalar Product)
- The dot product, also known as the scalar product, is a way of multiplying vectors.
- When you take the dot product of two vectors, you get a single number, not another vector. This result is called a scalar.
- The dot product is found by multiplying the magnitudes (lengths) of the two vectors and then multiplying that by the cosine of the angle between them. The result lies in the same plane as the two original vectors.
 .
. 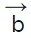 = |
= |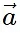 | |
| |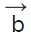 | cosθ
| cosθ - Here, |
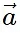 | is the magnitude of
| is the magnitude of 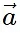 , |
, |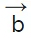 | is the magnitude of
| is the magnitude of 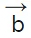 , and θ is the angle between them.
, and θ is the angle between them. - Depending on the angle between the vectors, the dot product can be a positive or negative number.
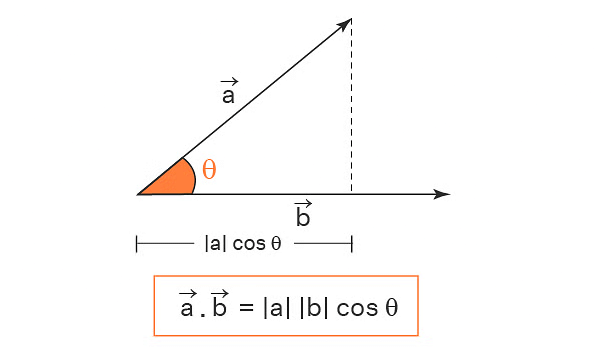 Dot Product of Vectors
Dot Product of Vectors
For the dot product of two vectors, the two vectors are expressed in terms of unit vectors, i, j, k, along the x, y, and z axes, then the scalar product is obtained as follows:
If 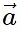 =a1^i+b1^j+c1^k and
=a1^i+b1^j+c1^k and 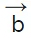 =a2^i+b2^j+c2^k, then
=a2^i+b2^j+c2^k, then
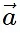 .
. 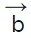 = (a1^i+b1^j+c1^k)(a2^i+b2^j+c2^k)
= (a1^i+b1^j+c1^k)(a2^i+b2^j+c2^k)
= (a1a2)(^i.^i)+(a1b2)(^i.^j)+(a1c2)(^i.^k)+(b1a2)(^j.^i)+(b1b2)(^j.^j)+(b1c2(^j.^k)+(c1a2)(^k.^i)+(c1b2)(^k.^j)+(c1c2)(^k.^k)
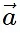 .
. 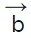 = a1a2+b1b2+c1c2
= a1a2+b1b2+c1c2
Properties of Dot Product
- Commutativity: A⋅B=B⋅A
- Distributivity over Vector Addition: A⋅(B+C)=A⋅B+A⋅C
- Scalar Multiplication: (kA)⋅B=k⋅(A⋅B)
- Orthogonality: A⋅B=0 if and only if vectors A and B are orthogonal.
Applications of Dot Product
- Cosine of the Angle between Vectors:
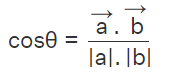
- Projection of Vectors:
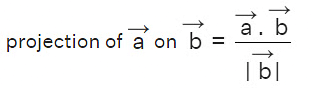
- Work Done in Physics:

Ex. Find the dot product of a= (1, 2, 3) and b= (4, −5, 6). What kind of angle the vectors would form?
Solution.
Using the formula of the dot products,
a.b = (a1b1 + a2b2 + a3b3)
You can calculate the dot product to be
= 1(4) + 2(−5) + 3(6)
= 4 − 10 + 18
= 12
Since a.b is a positive number, you can infer that the vectors would form an acute angle.
Cross Product (Vector Product)
- The cross product of two vectors, A and B, denoted as A × B, is a vector quantity obtained by applying the right-hand rule to the cross product of their magnitudes and the sine of the angle between them.
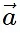 X
X 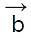 = |
= |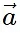 | |
| |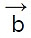 | sin(θ) nHere
| sin(θ) nHere 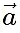 and
and 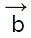 are two vectors. θ is the angle formed between
are two vectors. θ is the angle formed between 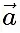 and
and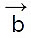 and ^n is the unit vector perpendicular to the plane containing both
and ^n is the unit vector perpendicular to the plane containing both 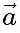 and
and 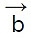 .
.
- When we do the cross-product, we get a new vector that is perpendicular (at a right angle) to the original two vectors.
- Let us assume that
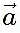 and
and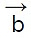 are two vectors, such that
are two vectors, such that 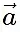 = a1^i+b1^j+c1^k and
= a1^i+b1^j+c1^k and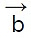 = a2^i+b2^j+c2^k then by using determinants, we could find the cross product and write the result as the cross-product formula using the following matrix notation.
= a2^i+b2^j+c2^k then by using determinants, we could find the cross product and write the result as the cross-product formula using the following matrix notation.
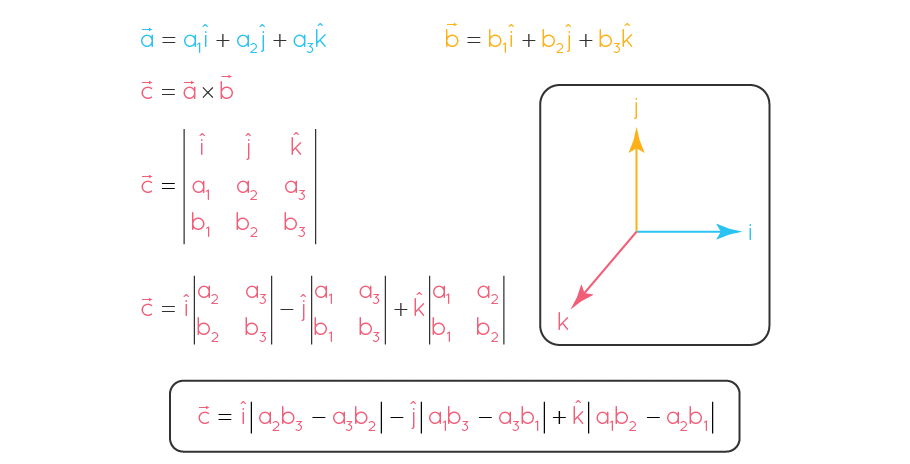 Cross Product of Vectors
Cross Product of Vectors
The cross-product of two vectors is also represented using the cross product formula as:
×
=^i(b1c2−b2c1)−^j(a1c2−a2c1)+^k(a1b2−a2b1)
Note: ^i,^j, and ^k are the unit vectors in the direction of x axis, y-axis, and z -axis respectively.
Properties
- Anti-Commutativity: A×B=−B×A
- Distributivity over Vector Addition: A×(B+C)=A×B+A×C
- Scalar Triple Product: A⋅(B×C)=B⋅(C×A)=C⋅(A×B)
Applications of Cross-Product
- Torque in Physics: Torque=r×F
- Magnetic Force: F=q(v×B)
- Angular Momentum: L=r×p
Ex. Find a unit vector that is perpendicular to both of the vectors a = i + 3j − 2k and b = 5i − 3k.
Solution. We know from the definition of the vector product that the vector a × b will be perpendicular to both a and b. So first of all we calculate a × b.
a × b =
= (3 × −3 − (−2) × 0)i − (1 × −3 − (−2) × 5)j + (1 × 0 − 3 × 5)k
= −9i − 7j − 15k
This vector is perpendicular both to a and b.
To convert a vector into a unit vector in the same direction we must divide it by its modulus.
The modulus of −9i − 7j − 15k is |a × b| = p (−9)2 + (−7)2 + (−15)2 = √ 355
So, finally, the required unit vector is
Other Applications of Product of Vectors
Triple Cross Product
Other Applications of Product of Vectors
The triple cross product involves the cross product of a vector with the result of another cross product of two vectors. The outcome is a new vector, and it lies in the plane formed by the original three vectors. If we have vectors a, b, and c,
The triple cross product of these vectors is expressed as (a×b)×c=(a⋅c)b−(b⋅c)a.
Area of a Parallelogram
The two adjacent sides of a parallelogram can be represented by the vectors a and b. The area of the parallelogram is the product of the base and the height. Considering the base as ∣a∣cosθ and the height as ∣b∣sinθ, the area is given by
Area=∣a∣⋅∣b∣⋅sinθ=a×b.
Volume of a Parallelepiped
A parallelepiped is a six-sided figure with parallelogram sides. The opposite side parallelograms are identical. The volume (V) of the parallelepiped can be obtained from the side lengths a, b, and c. The volume is calculated as
V=a⋅(b×c).
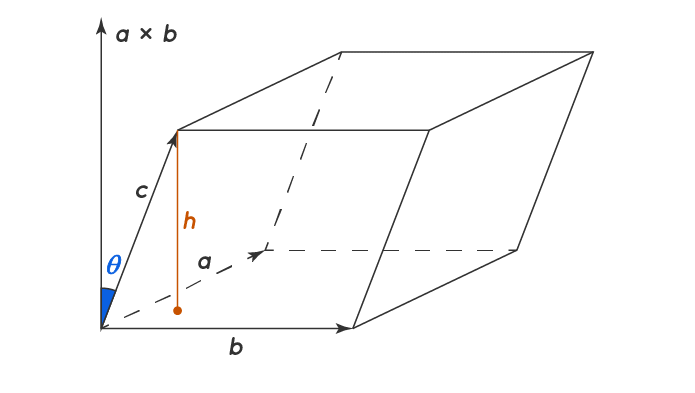 Parallelepiped
Parallelepiped
Ex. Find the volume of the parallelepiped with edges a = 3i+2j+k, b = 2i+j+k, and c = i + 2j + 4k.
Solution. We first evaluate the vector product b × c.
b × c =
= (1 × 4 − 1 × 2)i − (2 × 4 − 1 × 1)j + (2 × 2 − 1 × 1)k
= 2i − 7j + 3k
Then we need to find the scalar product of a with b × c.
a · (b × c) = (3i + 2j + k) · (2i − 7j + 3k) = 6 − 14 + 3 = −5
|
268 videos|774 docs|209 tests
|
FAQs on Product of Vectors - Physics for JEE Main & Advanced
| 1. What is the dot product of two vectors? |  |
| 2. How is the cross product of two vectors calculated? |  |
| 3. What are some applications of the product of vectors? |  |
| 4. How is the dot product related to vector projections? |  |
| 5. Can the dot product of two vectors be negative? |  |