Mathematics Exam > Mathematics Notes > Additional Topics for IIT JAM Mathematics > Pythagorean Theorem
Pythagorean Theorem | Additional Topics for IIT JAM Mathematics PDF Download
Pythagorean Theorem: a2+b2 = c2
In a right triangle, the sum of the squares of the two legs equals the square of the hypotenuse.
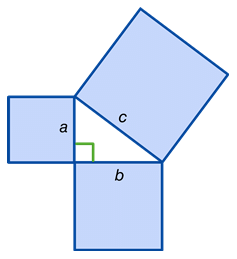
- Legs (a and b): the sides of the triangle adjacent to the right angle. They don't need to be the same length in order for this theorem to work.
- Hypotenuse (c): the side of the triangle opposite the right angle which, conveniently, is always the longest side.
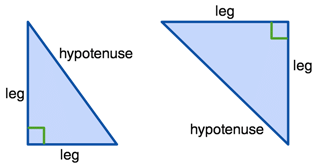
So, let's break this down. If you square each side of the triangle, the sum of the areas of the two legs squared is equal to the hypotenuse squared.
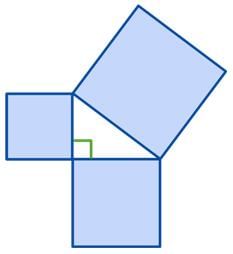
Here you can see it with numbers:
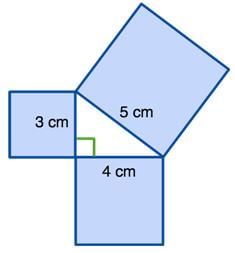
The area of the two smaller squares is (3 × 3 = 9 cm2) and (4 × 4 = 16 cm2).
The area of the larger square is equal to (5 × 5 = 25 cm2).
If you add the two smaller areas together, you get the area of the square of the hypotenuse (9 + 16 = 25 cm2).
The document Pythagorean Theorem | Additional Topics for IIT JAM Mathematics is a part of the Mathematics Course Additional Topics for IIT JAM Mathematics.
All you need of Mathematics at this link: Mathematics
FAQs on Pythagorean Theorem - Additional Topics for IIT JAM Mathematics
| 1. What is the Pythagorean Theorem? |  |
Ans. The Pythagorean Theorem is a mathematical formula that relates to right-angled triangles. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In equation form, it can be written as a^2 + b^2 = c^2, where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides.
| 2. How can the Pythagorean Theorem be used to find the length of a missing side in a right-angled triangle? | |
Ans. To find the length of a missing side in a right-angled triangle using the Pythagorean Theorem, you need to know the lengths of the other two sides. By substituting the known values into the equation a^2 + b^2 = c^2 and solving for the missing side length, you can determine the unknown side. For example, if you know the lengths of the two legs (a and b), you can find the length of the hypotenuse (c) using the theorem.
| 3. Can the Pythagorean Theorem be used in non-right-angled triangles? | |
Ans. No, the Pythagorean Theorem is only applicable to right-angled triangles. In a non-right-angled triangle, the sum of the squares of any two sides will always be greater than the square of the longest side. Therefore, the Pythagorean Theorem cannot be applied to find the lengths of sides in non-right-angled triangles.
| 4. What are some practical applications of the Pythagorean Theorem? | |
Ans. The Pythagorean Theorem has various practical applications in real life. It is commonly used in construction, architecture, and engineering to calculate distances, lengths, and angles. For example, it can be used to determine the length of a ladder needed to reach a certain height on a wall or to calculate the diagonal length of a rectangular room.
| 5. Who discovered the Pythagorean Theorem? | |
Ans. The Pythagorean Theorem is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery. However, it is important to note that the theorem was known and used by other civilizations, such as the Babylonians and Egyptians, even before Pythagoras. The theorem's name is derived from Pythagoras due to his contributions to the field of mathematics and his work in proving the theorem's validity.
Related Exams
About this Document
|
4.81/5 Rating |
|
Nov 22, 2024 Last updated |
Document Description: Pythagorean Theorem for Mathematics 2024 is part of Additional Topics for IIT JAM Mathematics preparation.
The notes and questions for Pythagorean Theorem have been prepared according to the Mathematics exam syllabus. Information about Pythagorean Theorem covers topics
like and Pythagorean Theorem Example, for Mathematics 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Pythagorean Theorem.
Introduction of Pythagorean Theorem in English is available as part of our Additional Topics for IIT JAM Mathematics
for Mathematics & Pythagorean Theorem in Hindi for Additional Topics for IIT JAM Mathematics course.
Download more important topics related with notes, lectures and mock test series for Mathematics
Exam by signing up for free. Mathematics: Pythagorean Theorem | Additional Topics for IIT JAM Mathematics
Description
Full syllabus notes, lecture & questions for Pythagorean Theorem | Additional Topics for IIT JAM Mathematics - Mathematics | Plus excerises question with solution to help you revise complete syllabus for Additional Topics for IIT JAM Mathematics | Best notes, free PDF download
Information about Pythagorean Theorem
In this doc you can find the meaning of Pythagorean Theorem defined & explained in the simplest way possible. Besides explaining types of
Pythagorean Theorem theory, EduRev gives you an ample number of questions to practice Pythagorean Theorem tests, examples and also practice Mathematics
tests
|
Explore Courses for Mathematics exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Viva Questions
,video lectures
,MCQs
,Important questions
,Objective type Questions
,Extra Questions
,past year papers
,mock tests for examination
,ppt
,Pythagorean Theorem | Additional Topics for IIT JAM Mathematics
,Summary
,practice quizzes
,Sample Paper
,shortcuts and tricks
,Pythagorean Theorem | Additional Topics for IIT JAM Mathematics
,Exam
,Free
,study material
,Semester Notes
,Previous Year Questions with Solutions
,Pythagorean Theorem | Additional Topics for IIT JAM Mathematics
;
Additional Information about Pythagorean Theorem for Mathematics Preparation
Pythagorean Theorem Free PDF Download
The Pythagorean Theorem is an invaluable resource that delves deep into the core of the Mathematics exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Pythagorean Theorem now and kickstart your journey towards success in the Mathematics exam.
Importance of Pythagorean Theorem
The importance of Pythagorean Theorem cannot be overstated, especially for Mathematics aspirants.
This document holds the key to success in the Mathematics exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Pythagorean Theorem Notes
Pythagorean Theorem Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Pythagorean Theorem.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Pythagorean Theorem Notes on EduRev are your ultimate resource for success.
Pythagorean Theorem Mathematics Questions
The "Pythagorean Theorem Mathematics Questions" guide is a valuable resource for all aspiring students preparing for the
Mathematics exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Pythagorean Theorem on the App
Students of Mathematics can study Pythagorean Theorem alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Pythagorean Theorem,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Pythagorean Theorem is prepared as per the latest Mathematics syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup