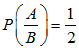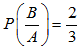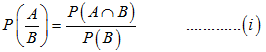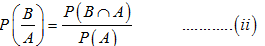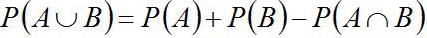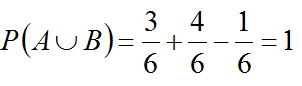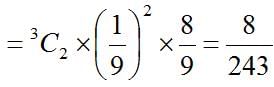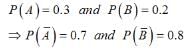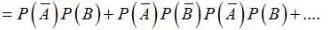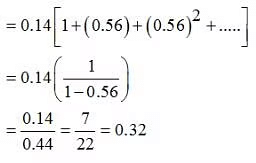Questions with Answers: Probability | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
Q.1. If 4 whole numbers taken at random are multiplied together show that the chance that the last digit in the product is 1,3,7, or 9 is 16/625.
If the last digit is 1,3,7,9 in the product then we can only select numbers whose last digit is 1,3,7 or 9 from 0,1,2,....9
Probability that a selected number ends with 1, 3, 7 or 9 = 4/10 = 2/5.Probability of selecting four such numbers = (2/5)4 = 16/625
Hence Proved.
Q.2. It is given that the events A and B are such that P(A) = 1/4, P(A|B) = 1/2 and P(B|A) = 2/3. Then P(B|A) = 2/3. Then P(B) is
(a) 1/2
(b) 1/6
(c) 1/3
(d) 2/3
Correct Answer Option (c)
Given that P(A) = 1/4,
andwe know,
and
Now, substitute the values in the formula, we get
(2/3) = P(B∩A)/ (1/4)
P(B∩A) = (2/3). (1/4)
P(B∩A) = 1/6
Substitute the values in (1), we get
P(A/B) = P(A∩B)/ P(B)
(1/2) = (1/6)/ P(B)
P(B) = (1/6). (2/1)
P(B) = 1/3
Q.3. A die is thrown. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then P (AUB) is
(a) 2/5
(b) 3/5
(c) 0
(d) 1
Correct Answer Option (d)
Since,
A = number > 3
A {4,5,6}
and B = number < 5
B = {1, 2, 3, 4}
∴ A∩B = {4}∴
⇒
Q.4. A pair of fair dice is thrown independently three times. The probability of getting a total of exactly 9 twice is
(a) 1/729
(b) 8/9
(c) 8/729
(d) 8/243
Correct Answer Option (d)
When two dice are thrown, the total number of sample space is 36
Probability of getting a total of 9 in a single throw
4/36 = 1/9
Hence, the probability of getting a score of exactly 9 twice
Q.5. Two aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane, is
(a) 0.06
(b) 0.14
(c) 0.32
(d) 0.7
Correct Answer Option (c)
Let the events,
A = 1st aeroplane hit the target
B =2nd aeroplane hit the target
And their corresponding probabilities are
Required Probability
= (0.7)(0.2) + (0.7)(0.8)(0.7)(0.2)+ (0.7)(0.8)(0.7)(0.8)(0.7)(0.2) + ....
|
1335 videos|1432 docs|834 tests
|
FAQs on Questions with Answers: Probability - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What is probability and how is it related to statistics? |  |
| 2. How is probability calculated? |  |
| 3. What is the difference between theoretical probability and experimental probability? |  |
| 4. What are independent and dependent events in probability? |  |
| 5. How can probability be applied in real-life situations? |  |