Ex-1.4 Integers, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
QUESTION 1:
Simplify each of the following:
3 − (5 − 6 ÷ 3)
ANSWER 1:
On applying the BODMAS rule, we get:
3 − (5 − 6 ÷ 3)
= 3 − (5 − 2) (On performing division)
= 3 − 3 (On performing subtraction)
= 0
QUESTION 2:
Simplify each of the following:
−25 + 14 ÷ (5 − 3)
ANSWER 2:
On applying the BODMAS rule, we get:
−25 + 14 ÷ (5 − 3)
= −25 + 14 ÷ 2 (On simplifying brackets)
= −25 + 7 (On performing division)
= −18
QUESTION 3:
Simplify each of the following:
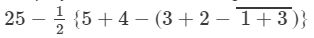
ANSWER 3:
On applying the BODMAS rule, we get:
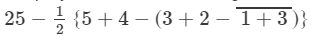
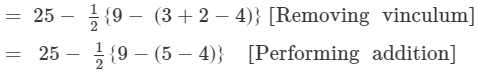
QUESTION 4:
Simplify each of the following:
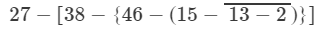
ANSWER 4:
On applying the BODMAS rule, we get:
27 −- [38 −- {46 −- (15 −-11)}] (On simplifying vinculum)
= 27 −- [38−- {46 −- 4}] (On simplifying parentheses)
= 27 −- [38 −- 42] (On simplifying braces)
= 27 −- (−-4) = 31
QUESTION 5:
Simplify each of the following:
36−[18−{14−(15−4 ÷2×2)}]36-18-{14-(15-4 ÷2×2)}
ANSWER 5:
On applying the BODMAS rule, we get:
36 −- [18 −- { 14 −- (15 −- 4 ÷ 2 × 2)}]
= 36 − [18 − {14 − (15 − 2 × 2)}] (On performing division)
= 36 −- [18 −- {14 −- (15 −- 4)}] (On performing multiplication)
= 36 −- [18 −- {14 −- 11}] (On simplifying parentheses)
= 36 −- [18 −- 3] (On simplifying braces)
= 36 −- 15
= 21
QUESTION 6:
Simplify each of the following:
45−[38−{60÷3−(6−9 ÷3)÷3}]45-38-{60÷3-(6-9 ÷3)÷3}
ANSWER 6:
On applying the BODMAS rule, we get:
45 −- [38 −- { 60 ÷ 3 −- (6 −- 9 ÷ 3) ÷ 3}]
= 45 −- [38 −- {60 ÷ 3 −- (6 −- 3) ÷ 3}] (On performing division)
= 45 −- [38 −- {60 ÷ 3 −- 3 ÷ 3}] (On simplifying parentheses)
= 45 −- [38 −- {60 ÷ 3 −- 1}] (On performing division)
= 45 −- [38 −- {20 −- 1}] (On performing division)
= 45 −- [38 −- 19] (On performing subtraction)
= 45 −- 19
= 26
QUESTION 7:
Simplify each of the following:
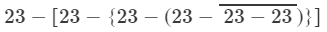
ANSWER 7:
On applying the BODMAS rule, we get:
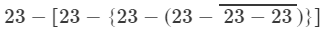
= 23 −- [23 −- {23 −- (23 −- 0}] (On simplifying vinculum)
= 23 −- [23 −- {23 −- 23}] (On simplifying parentheses)
= 23 −- [23 −- 0] (On simplifying braces)
= 23 −- 23 = 0
QUESTION 8:
Simplify each of the following:
Answer 8:
On applying the BODMAS rule, we get:
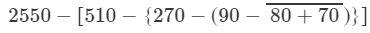
= 2550 −- [510 −- {270 −- (90 −- 150)}] (On simplifying vinculum)
= 2550 −- [510 −- { 270 −- (−- 60)}] (On simplifying parentheses)
= 2550 −- [510 −- 330] (On simplifying braces)
= 2550 −- 180
= 2370
Question 9:
Simplify each of the following:
Answer 9:
On applying the BODMAS rule, we get:
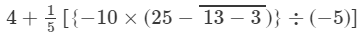
= 4 + 6
= 10
QUESTION 10:
Answer 10:
On applying the BODMAS rule, we get:
=22−(−2) [Removing braces]
= 22+2 = 24
Question 11:
Simplify each of the following:
nswer 11:
On applying the BODMAS rule, we get:
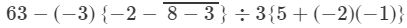
= 63 −- (−- 3) {−- 2 −- 5} ÷ 3 {5 + 2} (On simplifying vinculum)
= 63 −- (−- 3) (−- 7 ) ÷ 3 × 7 (On simplifying braces)
= 63 −- (21÷2121÷21)
= 63 −- 1
= 62
Question 12:
Simplify each of the following:
[29−(−2){6−(7−3)}]÷[3×{5+(−3)×(−2)}]
Answer 12:
On applying the BODMAS rule, we get:
[29 −- (−- 2) {6 −- (7 −- 3)}] ÷ [3 × { −- 3) × (−- 2)}]
= [29 −- (−- 2) {6 −- 4}] ÷ [3 × { 5 + 6}] (On simplifying parentheses)
= [29 −- (−- 2) (2)] ÷ [3 × 11] (On performing subtraction and addition)
= [29 + 4] ÷÷ 33 (On performing multiplication)
= 33 ÷÷ 33
= 1
Question 13:
Using brackets, write a mathematical expression for each of the following:
(i) Nine multiplied by the sum of two and five.
(ii) Twelve divided by the sum of one and three.
(iii) Twenty divided by the difference of seven and two.
(iv) Eight subtracted from the product of two and three.
(v) Forty divided by one more than the sum of nine and ten.
(vi) Two multiplied by one less than the difference of nineteen and six.
Answer 13:
(i) 9 (2 + 5)
(ii) 12 ÷ (1 + 3)
(iii) 20 ÷ (7 −- 2)
(iv) (2 × 3 ) −- 8
(v) 40 ÷ {(9 + 10) + 1}
(vi) 2 × {(19 −- 6) −- 1}
FAQs on Ex-1.4 Integers, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are integers? |  |
| 2. How to add integers? | |
| 3. Can we multiply two negative integers to get a positive integer? | |
| 4. How to subtract integers? | |
| 5. What are the properties of integers? | |
|
1.6K Views |
|
4.60/5 Rating |
|
Dec 22, 2024 Last updated |
|
Explore Courses for Class 7 exam
|
|
study material
,Previous Year Questions with Solutions
,Sample Paper
,MCQs
,video lectures
,ppt
,past year papers
,Extra Questions
,Class 7
,Objective type Questions
,practice quizzes
,Semester Notes
,Class 7
,Free
,Important questions
,Ex-1.4 Integers
,Class 7
,Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics
,Summary
,Ex-1.4 Integers
,Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics
,shortcuts and tricks
,Viva Questions
,Ex-1.4 Integers
,Exam
,Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics
,mock tests for examination
;
RD Sharma Solutions - Ex-1.4 Integers, Class 7, Math Free PDF Download
Importance of RD Sharma Solutions - Ex-1.4 Integers, Class 7, Math
RD Sharma Solutions - Ex-1.4 Integers, Class 7, Math Notes
RD Sharma Solutions - Ex-1.4 Integers, Class 7, Math Class 7 Questions
Study RD Sharma Solutions - Ex-1.4 Integers, Class 7, Math on the App
|
© EduRev
|
Education Revolution
|
|
