Ex-1.5 Real Numbers, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Q.1: Show that the following numbers are irrational.
(i) 7√5
Let us assume that 7√5 is rational. Then, there exist positive co primes a and b such that
7√5 = a/b
√5 = a/7b
We know that √5 is an irrational number
Here we see that √5 is a rational number which is a contradiction.
(ii) 6 + √2
Let us assume that 6 + √2 is rational. Then, there exist positive co primes a and b such that
6 + √2 = a/b
√2 = a/b − 6
√2 = 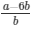
Here we see that √2 is a rational number which is a contradiction as we know that √2 is an irrational number
Hence 6 + √2 is an irrational number
(iii) 3 − √5
Let us assume that 3 − √5 is rational. Then, there exist positive co primes a and b such that
3 − √5 = a/b
√5 = 3 − a/b
√5 = 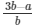
Here we see that √5 is a rational number which is a contradiction as we know that √5 is an irrational number
Hence 3 − √5 is an irrational number.
Q.2: Prove that the following numbers are irrationals.
Sol: (i) 2/√7
Let us assume that 2√7 is rational. Then, there exist positive co primes a and b such that
2√7 = a/b
√7 = 2b/a
√7 is rational number which is a contradiction
Hence 2√7 is an irrational number
(ii) 325√
Let us assume that 3/2√5 is rational. Then, there exist positive co primes a and b such that
3/2√5 = a/b
√5 = 3b/2a
√5 is rational number which is a contradiction
Hence 3/2√5 is irrational.
(iii) 4 + √2
Let us assume that 4 + √2 is rational. Then, there exist positive co primes a and b such that
4 + √2 = a/b
√2 = a/b − 4
√2 = 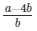
√2 is rational number which is a contradiction
Hence 4 + √2 is irrational.
(iv) 5√2
Let us assume that 5√2 is rational. Then, there exist positive co primes a and b such that
5√2 = ab
√2 = a/b − 5
√2 = 
√2 is rational number which is a contradiction
Hence 5√2 is irrational
Q.3: Show that 2 − √3 is an irrational number.
Sol: Let us assume that 2 − √3 is rational. Then, there exist positive co primes a and b such that
2 − √3 = a/b
√3 = 2 − a/b
Here we see that √3 is a rational number which is a contradiction
Hence 2 − √3 is irrational
Q.4: Show that 3 + √2 is an irrational number.
Sol: Let us assume that 3 + √2 is rational. Then, there exist positive co primes a and b such that
3 + √2 = a/b
√2 = a/b − 3
√2 = 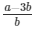
Here we see that √2 is a irrational number which is a contradiction
Hence 3 + √2 is irrational
Q.5: Prove that 4 − 5√2 is an irrational number.
Sol: Let us assume that 4 − 5√2 is rational. Then, there exist positive co primes a and b such that
4 − 5√2 = a/b
5√2 = a/b − 4
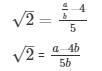
This contradicts the fact that √2 is an irrational number
Hence 4 − 5√2 is irrational
Q.6: Show that 5 − 2√3 is an irrational number.
Sol. Let us assume that 5 − 2√3 is rational. Then, there exist positive co primes a and b such that
5 − 2√3 = ab
2√3 = a/b − 5
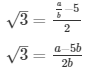
This contradicts the fact that √3 is an irrational number
Hence 5 − 2√3 is irrational
Q.7: Prove that 2√3 − 1 is an irrational number.
Sol: Let us assume that 2√3 − 1 is rational. Then, there exist positive co primes a and b such that
2√3 − 1 = a/b
2√3 = a/b + 1
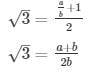
This contradicts the fact that √3 is an irrational number
Hence 5 − 2√3 is irrational
Q.8: Prove that 2 − 3√5 is an irrational number.
Sol: Let us assume that 2 − 3√5 is rational. Then, there exist positive co primes a and b such that
2 − 3√5 = a/b
3√5 = a/b − 2
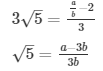
This contradicts the fact that √5 is an irrational number
Hence 2 − 3√5 is irrational
Q.9: Prove that √5 + √3 is irrational.
Sol: Let us assume that √5 + √3 is rational. Then, there exist positive co primes a and b such that
√5 + √3 = a/b
√5 = a/b − √3
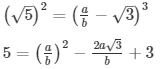
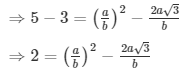
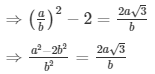
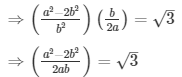
Here we see that √3 is a rational number which is a contradiction as we know that √3 is an irrational number
Hence √5 + √3 is an irrational number
Q.10: Prove that √3 + √4 is irrational.
Sol: Let us assume that √3 + √4 is rational. Then, there exist positive co primes a and b such that
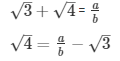

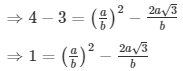
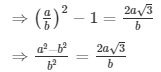
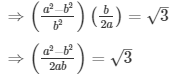
Here we see that √3 is a rational number which is a contradiction as we know that √3 is an irrational number
Hence √3 + √4 is an irrational number
Q.11: Prove that for any prime positive integer p, √p is an irrational number.
Sol: Let us assume that √p is rational. Then, there exist positive co primes a and b such that
√p = a/b
p = (a/b)2
⇒ p = a2/b2
⇒ pb2 = a2
⇒ p|a2
⇒ p|a
⇒ a = pcforsomepositiveintegerc
⇒ b2p = a2
⇒ b2p = p2c2 ( ∵ a = pc )
⇒ p|b2 (since p|c2p)
⇒ p|b
⇒ p|a and p|b
This contradicts the fact that a and b are co primes
Hence √p is irrational
Q.12: If p, q are prime positive integers, prove that √p + √q is an irrational number.
Sol: Let us assume that √p + √q is rational. Then, there exist positive co primes a and b such that

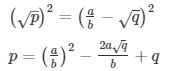
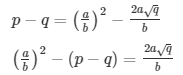
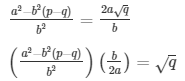
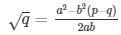
Here we see that √q is a rational number which is a contradiction as we know that √q is an irrational number
Hence √p + √q is an irrational number
|
5 videos|292 docs|59 tests
|
FAQs on Ex-1.5 Real Numbers, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What is the importance of studying Real Numbers in Class 10 Mathematics? |  |
| 2. What are the different types of Real Numbers? |  |
| 3. How to represent Real Numbers on a number line? |  |
| 4. How to determine if a given number is rational or irrational? |  |
| 5. What are the properties of Real Numbers? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















