Ex-3.2 Pair Of Linear Equations In Two Variables (Part - 1), Class 10, Math RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Solve the following system of equations graphically:
Q1. x + y = 3; 2x + 5y = 12
Sol: 2x + 5y = 12
We have,
x + y = 3
When y = 0 we have x = 3
When x = 0 we have y = 3
Thus we have the following table giving points on the line x + y = 3
| X | 0 | 3 |
| Y | 3 | 0 |
Now, 2 + 5y = 12
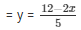
When x = 1, we have
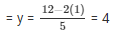
Thus we have the following table giving points on the line 2x + 5y = 12
| X | 1 | -4 |
| Y | 2 | 4 |
Graph of the equation x + y = 3 and 2x + 5y = 12 is

Clearly two lines intersect at a point P (1,2)
Hence x = 1 and y = 2
Q2: x- 2y = 5, 2x + 3y = 10
Sol: We have, x- 2y = 5 and 2x + 3y = 10
Now, x- 2y = 5
= x = 5 + 2y
When y = 0 then, x = 5
When y = -2 then, x = 1
Thus, we have the following table giving points on the line x-2y = 5
| X | 5 | -1 |
| Y | 0 | -2 |
Now , 2x + 3y = 10 = x = 
When y = 0, then x = 5
When y = 2 , then x = 2Thus, we have the following table giving points on the line 2x + 3y = 10
| X | 5 | 2 |
| Y | 0 | 2 |
Graph of the equation x-2y = 5 and 2x + 3y = 10

Clearly, two lines intersect at a point P (5,0)
Hence x = 5 and y = 0
Q3: 3x + y + 1 = 0, 2x-3y + 8 = 0
Sol: We have, 3x + y + 1 = 0 and 2x-3y + 8 = 0
Now 3x + y + 1 = 0
= y = -1-3x
When x = 0 then, x = -1
When y = -1 then, x = 2
Thus, we have the following table giving points on the line x-2y = 5
| X | -1 | 0 |
| Y | 2 | -1 |
Now, 2x-3y + 8 = 0
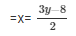
When y = 0, then x = -4
When y = 2 , then x = 1Thus, we have the following table giving points on the line 2x + 3y = 10
| X | -4 | -1 |
| Y | 0 | -2 |
Graph of the equation 3x + y + 1 = 0 and 2x-3y + 8 = 0

Clearly two lines intersect at a point P (-1, 2)
Hence x = -1 and y = 2
Q4: 2x + y-3 = 0, 2x-3y-7 = 0
Sol: We have, 2x + y-3 = 0 and 2x-3y-7 = 0
Now 2x + y-3 = 0
= y = 3-2x
When x = 0 then, x = 3
When x = 1 then, x = 1
Thus, we have the following table giving points on the line 2x + y-3 = 0
| X | 0 | 1 |
| Y | 3 | 1 |
Now, 2x-3y-7 = 0
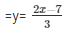
When x = 0, then y = 1
When x = 2, then y = -1Thus, we have the following table giving points on the line 2x + 3y = 10
| X | 2 | 5 |
| Y | -1 | 1 |
Graph of the equation 2x + y-3 = 0 and 2x-3y-7 = 0
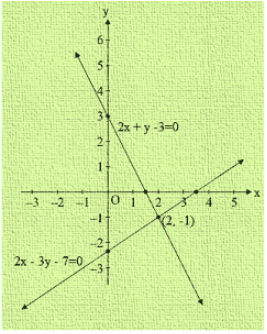
Clearly two lines intersect at a point P (2,-1)
Hence x = 2 and y = -1
Q5. x + y = 6
x-y = 2
Sol. We have, x + y = 6 and x-y = 2
Now x + y = 6
= y = 6-x
When x = 2 then, y = 4
When x = 3 then, y = 3
Thus, we have the following table giving points on the line x + y = 6
| X | 2 | 3 |
| Y | 4 | 3 |
Now , x-y = 2
= y = x-2
When x = 0, then y = -2
When x = 2 , then y = 0Thus, we have the following table giving points on the line 2x + 3y = 10
| X | 0 | 2 |
| Y | 2 | 0 |
Graph of the equation x + y = 6 and x-y = 2
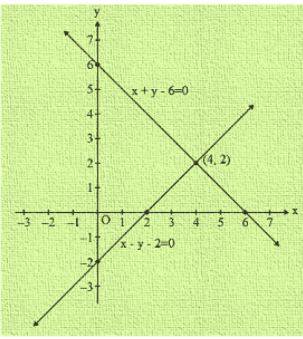
Clearly two lines intersect at a point P (4,2)
Hence x = 4 and y = 2
Q6. x-2y = 6
3x-6y = 0
Sol. We have, x-2y = 6 and 3x-6y = 0
Now x-2y = 6
= x = 6 + 2y
When y = -2 then, x = 2
When y = -3 then, x = 0
Thus, we have the following table giving points on the line x-2y = 6
| X | 2 | 0 |
| Y | -2 | -3 |
Now , 3x-6y = 0
= x = 2y
When y = 0, then y = 0
When y = -1 , then x = 2
Thus, we have the following table giving points on the line 3x-6y = 0
| X | 0 | 2 |
| Y | 0 | 1 |
Graph of the equation x-2y = 6 and 3x-6y = 0
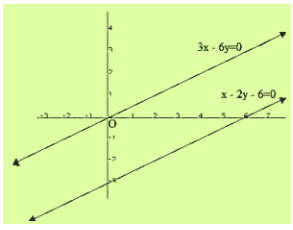
Clearly two lines are parallel to each other. So, the two lines have no common point.
Hence the given system has no solutions.
Q7. x + y = 4
2x-3y = 3
Sol. We have, x + y = 4 and 2x-3y = 3
Now x + y = 4
= x = 4-y
When y = 0 then, x = 4
When y = 2 then, x = 2
Thus, we have the following table giving points on the line x + y = 4
| X | 4 | 2 |
| Y | 0 | 2 |
Now , 2x-3y = 3

When y = 1, then x = 3
When y = -1 , then x = 0
Thus, we have the following table giving points on the line 2x-3y = 3
| X | 3 | 0 |
| Y | 1 | -1 |
Graph of the equation x + y = 4 and 2x-3y = 3
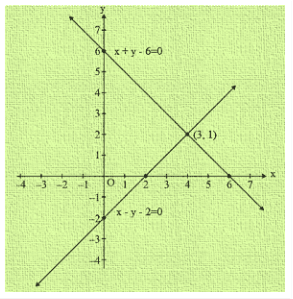
Clearly two lines intersect at a point P(3,1)
Hence x = 3 and y = 1
Q8. 2x + 3y = 4
x -y + 3 = 0
Sol. So we have, 2x + 3y = 4 and x-y + 3 = 0
Now 2x + 3y = 4
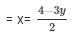
When y = 0 then, x = 2
When y = 2 then, x = -1
Thus, we have the following table giving points on the line x + y = 4
| X | -1 | 2 |
| Y | 2 | 0 |
Now , x-y + 3 = 0
= x = y-3
When y = 3, then x = 0
When y = 4, then x = 1
Thus, we have the following table giving points on the line x-y + 3 = 0
| X | 0 | 1 |
| Y | 3 | 4 |
Graph of the equation 2x + 3y = 4 and x-y + 3 = 0
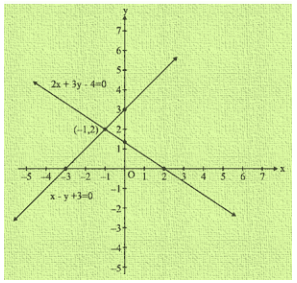
Clearly two lines intersect at (-1, 2)
Hence x = -1 and y = 2 is the solution of the given system of equations.
Q9. 2x-3y + 13 = 0
3x-2y + 12 = 0
Sol. So we have 2 x-3y + 13 = 0 and 3 x-2y + 12 = 0
Now, 2x-3y + 13 = 0
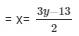
When y = 1 then, x = -5
When y = 3 then, x = -2
Thus, we have the following table giving points on the line 2x-3y + 13 = 0
| X | -5 | -2 |
| Y | 1 | 3 |
Now, 3x-2y + 12 = 0

When y = 0, then x = -14
When y = 3, then x = -2
Thus, we have the following table giving points on the line x-y + 3 = 0
| X | -4 | -2 |
| Y | 0 | 3 |
Graph of the equation 2x-3y + 14 = 0 and 3x-2y + 12 = 0
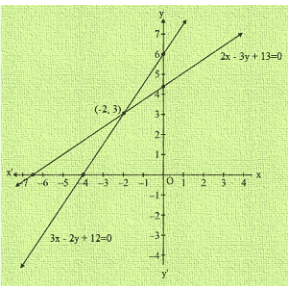
Clearly two lines intersect at (-2, 3)
Hence x = -2 and y = 3 is the solution of the given system of equations.
Q10. 2x + 3y + 5 = 0
3x + 2y-12 = 0
Sol. So we have 2x + 3y + 5 = 0 and 3x + 2y- 12 = 0
Now, 2x + 3y + 5 = 0
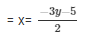
When y = 1 then, x = -4
When y = -1 then, x = -1
Thus, we have the following table giving points on the line 2x + 3y + 5 = 0
| X | -4 | -1 |
| Y | 1 | -1 |
Now, 3x + 2y-12 = 0
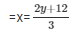
When y = 0, then x = 4
When y = 3, then x = 6
Thus, we have the following table giving points on the line 3x-2y-12 = 0
| X | 4 | 6 |
| Y | 0 | 3 |
Graph of the equation 2x + 3y + 5 = 0 and 3x + 2y-12 = 0

Clearly two lines intersect at (2, 3)
Hence x = 2 and y = 3 is the solution of the given system of equations.
Q11. 2x + 3y = 6
4x + 6y = 12
Sol. So we have 2x + 3y = 6 and 4x + 6y = 12
Now, 2x + 3y = 5
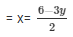
When y = 0 then, x = 3
When y = 2 then, x = 0
Thus, we have the following table giving points on the line 2x + 3y = 6
| X | 0 | 3 |
| Y | 2 | 0 |
Now, 4x + 6y = 12
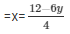
When y = 0, then x = 3
When y = 2, then x = 0
Thus, we have the following table giving points on the line 4x + 6y = 12
| X | 0 | 3 |
| Y | 2 | 0 |
Graph of the equation 2x + 3y = 6 and 4x + 6y = 12
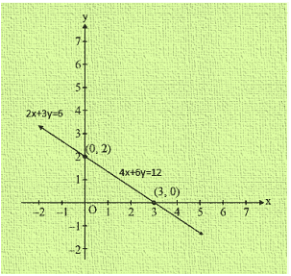
Thus the graphs of the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
Q12. x-2y = 5
3x-6y = 15
Sol. So we have x-2y = 5 and 3x-6y = 15
Now, x-2y = 5
= x = 2y + 5
When y = -1 then, x = 3
When y = 0 then, x = 5
Thus, we have the following table giving points on the line x-2y = 5
| X | 3 | 5 |
| Y | 1 | 0 |
Now, 3x-6y = 15
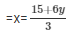
When y = -2, then x = 1
When y = -3, then x = -1
Thus, we have the following table giving points on the line 3x-6y = 15
| X | 1 | -1 |
| Y | -2 | -3 |
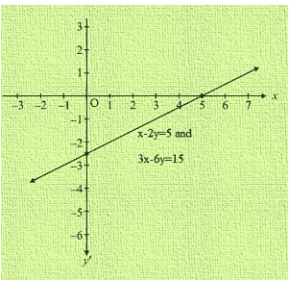
Q13. 3x + y = 8
6x + 2y = 16
Sol. So we have 3x + y = 8 and 6x + 2y = 16
Now, x-2y = 5
= y = 8-3x
When x = 2 then, y = 2
When x = 3 then, y = -1
Thus, we have the following table giving points on the line 3x + y = 8
| X | 2 | 3 |
| Y | 2 | -1 |
Now, 6x + 2y = 16
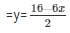
When x = 1, then y = 5
When x = 3, then y = -1
Thus, we have the following table giving points on the line 6x + 2y = 16
| X | 1 | 3 |
| Y | 5 | -1 |
Graph of the given equation
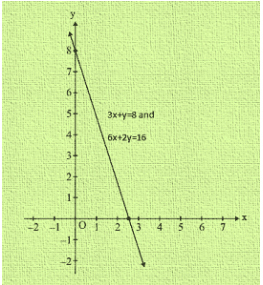
Thus, the graphs of the two equations are coincident
Hence, the system of equations has infinitely many solutions.
Q14. X-2y + 11 = 0
3x + 6y + 33 = 0
Sol. So we have x-2y + 11 = 0 and 3x + 6y + 33 = 0
Now, x-2y + 11 = 0
= x = 2y-11
When y = 5 then, x = -1
When y = 4 then, x = -3
Thus, we have the following table giving points on the line x-2y + 11 = 0
| X | -1 | -3 |
| Y | 5 | 4 |
Now, 3x-6y + 33 = 0

When y = 6, then x = -1
When y = 5, then x = -1
Thus, we have the following table giving points on the line 3x-6y + 33 = 0
| X | 1 | -1 |
| Y | 6 | 5 |
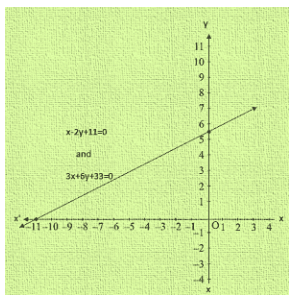
Thus, the graphs of the two equations are coincident
Hence, the system of equations has infinitely many solutions.
Q15. 3x-5y = 20
6x-10y = -40
Sol. So we have 3x-5y = 20 and 6x-10y = -40
Now, 3x-5y = 20
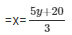
When y = -1 then, x = 5
When y = -4 then, x = 0
Thus, we have the following table giving points on the line 3x-5y = 20
| X | 5 | 0 |
| Y | -1 | -4 |
Now, 6x-10y = -40
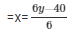
When y = 4, then x = 0
When y = 1, then x = -5
Thus, we have the following table giving points on the line 6x-10y = -40
| X | 0 | -5 |
| Y | 4 | 1 |
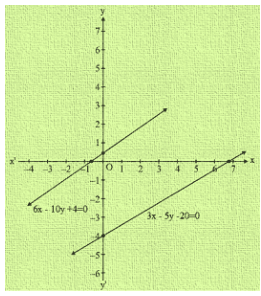
Clearly, there is no common point between these two lines.
Hence, given systems of equations is in consistent.
Q16. x-2y = 6
3x-6y = 0
Sol. So we have x-2y = 6 and 3x-6y = 0
Now, x-2y = 6
= x = 6 + 2y
When y = 0 then, x = 6
When y = -2 then, x = 2
Thus, we have the following table giving points on the line x-2y = 6
| X | 6 | 2 |
| Y | 0 | -2 |
Now, 3x-6y = 0
= x = 2y
When y = 0, then x = 0
When y = 1, then x = 2
Thus, we have the following table giving points on the line 3x-6y = 0
| X | 0 | 2 |
| Y | 0 | 1 |

We find the lines represented by equations x-2y = 6 and 3x-6y = 0 are parallel. So, the two lines have no common point.
Hence, the given system of equations is in-consistent.
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















