Ex-3.3 Pair Of Linear Equations In Two Variables (Part - 3), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 34
x + y = 5xy
3x + 2y = 13xy
Sol.
The given system of equations is:
x + y = 5xy ………………….. (i)
3x + 2y = 13xy……………… (ii)
Multiplying equation (i) by 2 and equation (ii) 1 we get,
2x + + 2y = 10xy ………………… (iii)
3x + 2y = 13xy ……………………. (iv)
Subtracting equation (iii) from equation (iv) we get,
3x − 2x = 13xy − 10xy
= x = 3xy
= x/3x = y
= 1/3 = y
Putting y = 1/3 = y in equation (i) we get,
= x + y = 5(x)( 1/3)
= x + x/3x = 5x/3
= 2x = 1
= x = 1/2 = y
Hence Solution of the given system of equation is 1/2 and 1/3
Question 35. x + y = xy
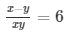
Sol. x + y = xy ………………………………….. (i)
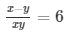 ………………….. (ii)
………………….. (ii)
Adding equation (i) and (ii) we get,
2x = 2xy + 6xy
= 2x = 6xy
= y = x + y = xy
= y = 1/4
Putting = y = 1/4 in equation (i) , we get,
= x + 1/4 = 2x(1/4)
= x = − 1/2
Hence the Solution of the given system of equation is = x = − 1/2
And y = 1/4 respectively.
Question 36. 2(3u − v) = 5uv
2(u + 3v) = 5uv
Solution. 2(3u − v) = 5uv
= 6u − 2v = 5uv …………………. (i)
2(u + 3v) = 5uv
2u + 6v = 5uv …………………….. (ii)
Multiplying equation (i) by 3 and equation (ii) by 1 we get,
18u − 6v = 15uv …………………….. (iii)
2u + 6v = 5uv ………………………….. (iv)
Adding equation (iii) and equation (iv) we get,
18u + 2u = 15uv + 5uv
= v = 1
Putting v = 1 in equation (i) we get,
6u − 2 = 5u
= u = 2
Hence the Solution of the given system of Solution of equation is 2 and 1 respectively.
Question 37.
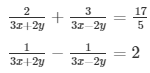
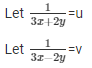
Sol. Then the given system of equation becomes:
2u + 3v = − 17/5 ………………………..(i)
5u − v = 2 ……………………… (ii)
Multiplying equation (ii) by 3
Adding equation (iv) and equation (iii) , we get
15u − 2u = − 17/5 + 5
= 13u = 13/5
= u = 1/5
Putting u = 1/5 in equation (i)
5(1/5) + v = − 2
= v = 1
Now,
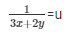
= 3x + 2y = 5 ……………..(iv)
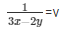
= 3x − 2y = 1 …………………..(v)
Adding equation (iv) and (v) we get,
6x = 6
= x = 1
Putting the value of x in equation (v) we get,
3 + 2y = 5
= y = 1
The Solutions of the given system of equation are 1 and 1 respectively.
Question 38.
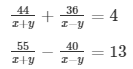
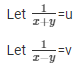
Sol. Then the given system of equation becomes:
44u + 30v = 10 ……………………….. (i)
55u + 40v = 13 ………………………(ii)
Multiplying equation (i) by 4 and (ii) by 3
176u + 120v = 40 ……………………… (iii)
165u + 120v = 39 ……………………… (iv)
Subtracting equation (iv) from (iii) we get,
176 − 165u = 40 − 39
= u = 1/11
Putting the value of u in equation (i)
44(1/11) + 30v = 10
= 4 + 30v = 10
= 30v = 6
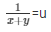
= x + y = 11……………..(v)
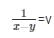
= x − y = 5 …………………..(vi)
Adding equation (v) and (vi) we get,
2x = 16
= x = 8
Putting the value of x in equation (v)
8 + y = 11
= y = 3
The Solutions of the given system of equation are 8 and 3 respectively.
Question 40
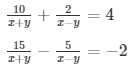
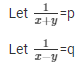
Sol. Then the given system of equation becomes:
10p + 2q = 4 ……………………….. (i)
15p − 5q = − 2 ………………………(ii)
Multiplying equation (i) by 4 and (ii) by 3
176u + 120v = 40 ……………………… (iii)
165u + 120v = 39 ……………………… (iv)
Using cross multiplication method we get,
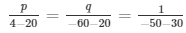
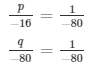
p = 1/5 and q = 1
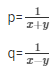
x + y = 5…………………….. 3
x − y = 1 ……………………..4
Adding equation 3 and 4 we get,
x = 3
Substituting the value of x in equation 3 we get,
y = 2
The Solution of the given system of Solution is 3 and 2 respectively.
Question 41
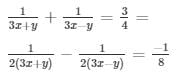
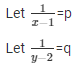
Sol. Then the given system of equation becomes:
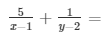 2 ………………………………..1
2 ………………………………..1
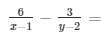 1……………………………………. 2
1……………………………………. 2
Can be written as 5p + q = 2 ………………………………… 3
6p − 3q = 1 ………………………………………. 4
Equation 3 and 4 from a pair of linear equation in the general form. Now, we can use any method to solve these equations.
We get p = 1/3
q = 1/3
Substituting the  for p , we have
for p , we have
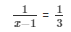
x − 1 = 3
x = 4

y − 2 = 3
y = 5
The Solution of the required pair of equation is 4 and 5 respectively.
Question 42
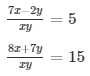
Sol. 7/y − 2/x = 5…………………………..1
8/y + 7/x = 15……………………………2
Let 1/x = p
Let 1/y = q
The given equation s reduce to:
− 2p + 7q = 5
= − 2p + 7q − 5 = 0 ……………………………….. 3
7p + 8q = 15
= 7p + 8q − 15 = 0 …………………………… 4
Using cross multiplication method we get,
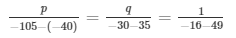
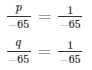
p = 1 and q = 1
p = 1/x
q = 1/y
x = 1 and y = 1
Question 43. 152x − 378y = − 74
− 378x + 152y = − 604
Sol. 152x − 378y = − 74 ……………………………. 1
− 378x + 152y = − 604 …………………………. 2
Adding the equations 1 and 2 , we obtain
− 226x − 226y = − 678
= x + y = 3 ……………………….. 3
Subtracting the equation 2 from equation 1, we obtain
530x + 530y = 530
x − y = 1 …………………………….4
Adding equations 3 and 4 we obtain,
2x = 4
= x = 2
Substituting the value of x in equation 3 we obtain y = 1
Question 44. 99x + 101y = 409
101x + 99y = 501
Sol. The given system of equation are :
99x + 101y = 409 ………………………….1
101x + 99y = 501…………………………….. 2
Adding equation 1 and 2 we get ,
99x + 101x + 101y + 99y = 49 + 501
= 200(x + y) = 1000
= x + y = 5 ……………………….. 3
Subtracting equation 1 from 2
101x − 99x + 99y − 101y = 501 − 499
= 2(x − y) = 2
= x − y = 1 ………………………………. 4
Adding equation 3 and 4 we get,
2x = 6
= x = 3
Putting x = 3 in equation 3 we get,
3 + y = 5
= y = 2
The Solution of the given system of equation is 3 and 2 respectively.
Question 45. 23x − 29y = 98
29x − 23y = 110
Sol. 23x − 29y = 98 ………………………………1
29x − 23y = 110 ………………………………… 2
Adding equation 1 and 2 we get,
= 6(x + y) = 12
= x + y = 2 ………………………3
Subtracting equation 1 from 2 we get,
52(x − y) = 208
= x − y = 4 ……………………………. 4
Adding equation 3 and 4 we get,
2x = 6
= x = 3
Putting the value of x in equation 4
3 + y = 2
= y = − 1
The Solution of the given system of equation is 3 and − 1 respectively.
Question 46. x − y + z = 4
x − 2y − 2z = 9
2x + y + 3z = 1
Sol. x − y + z = 4 …………………………..1
x − 2y − 2z = 9…………………………..2
2x + y + 3z = 1……………………………3
From equation 1
z = 4 − x + y
z = − x + y + 4
Subtracting the value of the z in equation 2 we get,
x − 2y − 2( − x + y + 4) = 9
= x − 2y + 2x − 2y − 8 = 8
= 3x − 4y = 17 …………………………….. 4
Subtracting the value of z in equation 3, we get,
2x + y + 3( − x + y + 4) = 1
= 2x + y + 3x + 3y + 12 = 1
= − x + 4y = − 11
Adding equation 4 and 5 we get,
3x − x − 4y + 4y = 17 − 11
= 2x = 6
= x = 3
Putting x = 3 in equation 4, we get,
9 − 4y = 17
= − 4y = 17 − 9
= y = − 2
Putting x = 3 and y = − 2 in z = − x + y + 4 , we get,
Z = − 3 − 2 + 4
= − 1
The Solution of the given system of equation are 3 , − 2 and − 1 respectively.
Question 47. x − y + z = 4
x + y + z = 2
2x + y − 3z = 0
Sol. x − y + z = 4 ………………………………….1
x + y + z = 2……………………………………..2
2x + y − 3z = 0………………………………………3
From equation 1
= z = − x + y + 4
Substituting z = − x + y + 4 in equation 2 , we get ,
= x + y + ( − x + y + 4) = 2
= x + y − x + y + 4 = 2
= 2y = 2
= y = 1
Substituting the value of z in equation 3
2x + y − 3( − x + y + 4) = 0
= 2x + y + 3x − 3y − 12 = 0
= 5x − 2y = 12 ………………………………. 4
Putting the y = − 1 in equation 4
5x − 2( − 1) = 12
5x = 10
= x = 2
Putting x = 2 and y = − 1 in z = − x + y + 4
Z = − 2 − 1 + 4
= 1
The Solution of the given system of equations are 2 , − 1 and 1 respectively.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-3.3 Pair Of Linear Equations In Two Variables (Part - 3), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are linear equations in two variables? |  |
| 2. How many solutions can a pair of linear equations have? |  |
| 3. How can we solve a pair of linear equations graphically? |  |
| 4. What is the substitution method for solving a pair of linear equations? |  |
| 5. Can a pair of linear equations have more than one unique solution? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















