Ex-4.6 Triangles, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
1. Triangles ABC and DEF are similar.
(i) If area of (ΔABC) = 16 cm2 , area (ΔDEF) = 25 cm2 and BC = 2.3 cm, find EF.
(ii) If area (ΔABC) = 9 cm2 , area (ΔDEF) = 64 cm2 and DE = 5.1 cm, find AB.
(iii) If AC = 19 cm and DF = 8 cm, find the ratio of the area of two triangles.
(iv) If area of (ΔABC) = 36 cm2 , area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
(v) If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the area of two triangles.
Answer:
(i) We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
arΔABC/arΔDEF = (BC/EF)2
16/25 = (2.3/EF)2
4/5 = 2.3/EF
EF = 2.875 cm
(ii) arΔABC/arΔDEF = (AB/DE)2
9/64 = (AB/DE)2
3/8 = AB/5.1
AB = 1.9125 cm
(iii) arΔABC/arΔDEF = (AC/DF)2
arΔABC/arΔDEF = (198)2
arΔABC/arΔDEF = (361/64)
(iv) arΔABC/arΔDEF = (AB/DE)2
36/64 = (AB/DE)2
6/8 = AB/6.2
AB = 4.65 cm
(v) arΔABC/arΔDEF = (AB/DE)2
arΔABC/arΔDEF = (1.2/1.4)2
arΔABC/arΔDEF = (36/49)
2. In the fig 4.178, ΔACB is similar to ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm, AP = 2.8 cm, find CA and AQ. Also, find the Area of ΔACB: Area of ΔAPQ.
Answer: Given: ΔACB is similar to ΔAPQ
BC = 10 cm
PQ = 5 cm
BA = 6.5 cm
AP = 2.8 cm
Find:
(1) CA and AQ
(2) Area of ΔACB: Area of ΔAPQ
(1) It is given that ΔACB – ΔAPQ
We know that for any two similar triangles the sides are proportional. Hence
AB/AQ = BC/PQ = AC/AP
AB/AQ = BC/PQ
6.5/AQ = 10/5
AQ = 3.25 cm
Similarly,
BC/PQ = CA/AP
CA/2.8 = 10/5
CA = 5.6 cm
(2) We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
arΔACQ/arΔAPQ = (BC/PQ)2
= (10/5)2
= (2/1)2
= 4/1
3. The areas of two similar triangles are 81 cm² and 49 cm² respectively. Find the ration of their corresponding heights. What is the ratio of their corresponding medians?
Answer: Given: The area of two similar triangles is 81cm2 and 49cm2 respectively.
To find:
(1) The ratio of their corresponding heights.
(2) The ratio of their corresponding medians.
(1) We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
ar(triangle1)/ar(triangle2) = (altitude1/altitude2)2
81/49 = (altitude1/altitude2)2
Taking square root on both sides, we get
9/7 = altitude1/altitude2
Altitude 1: altitude 2 = 9: 7
(2) We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their medians.
ar(triangle1)/ar(triangle2) = (median1/median2)2
81/49 = (median1/median2)2
Taking square root on both sides, we get
9/7 = median1/median2
Median 1: median 2 = 9: 7
4. The areas of two similar triangles are 169 cm2 and 121 cm2respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
Answer: Given:
The area of two similar triangles is 169cm2 and 121cm2 respectively. The longest side of the larger triangle is 26cm.
To find:
Longest side of the smaller triangle
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
ar(larger triangle)/ar(smaller triangle) = (side of the larger triangle/side of the smaller triangle)2
169/121 = (side of the larger triangle side of the smaller triangle)2
Taking square root on both sides, we get
13/11 = side of the larger triangle/side of the smaller triangle
13/11 = 26/side of the smaller triangle
Side of the smaller triangle = 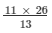 = 22 cm
= 22 cm
Hence, the longest side of the smaller triangle is 22 cm.
5. The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
Answer: Given:
The area of two similar triangles is 25cm2 and 36cm2 respectively. If the altitude of first triangle 2.4cm.
To find:
The altitude of the other triangle
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
ar(triangle1)/ar(triangle2) = (altitude1/altitude2)2
25/36 = (2.4/altitude2)2
Taking square root on both sides, we get
5/6 = 2.4/altitude2
Altitude 2 = 2.88 cm
Hence, the corresponding altitude of the other is 2.88 cm.
6. ABC is a triangle in which ∠ A = 90°, AN ⊥ BC, BC = 12 cm and AC = 5 cm. Find the ratio of the areas of ΔANC and ΔABC.
Answer: Given:
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively.
To find:
Ratio of areas of triangle
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
ar(triangle1)/ar(triangle2) = (altitude1/altitude2)2
ar(triangle1)/ar(triangle2) = (6/9)2
ar(triangle1)/ar(triangle2) = 36/81
ar(triangle1)/ar(triangle2) = 4/9
ar (triangle 1): ar (triangle 2) = 4: 9
Hence, the ratio of the areas of two triangles is 4: 9.
7. ABC is a triangle in which ∠A∘,AN⊥BC, BC = 12 cm and AC = 5 cm. Find the ratio of the areas of ΔANC and ΔABC.
Answer: Given:
In ΔABC, ∠A = 90∘, AN ⊥ BC, BC = 12 cm and AC = 5 cm.
To find:
Ratio of the triangles ΔANC and ΔABC.
In ΔANC and ΔABC,
∠ACN = ∠ACB (Common)
∠A = ∠ANC (90∘)
Therefore, ΔANC–ΔABC (AA similarity)
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Therefore,
Ar(ΔANC)/Ar(ΔABC) = (AC/BC)2
Ar(ΔANC)/Ar(ΔABC) = (5cm/12cm)2
Ar(ΔANC)/Ar(ΔABC) = 25/144
8. In Fig, DE || BC
(i) If DE = 4m, BC = 6 cm and Area (ΔADE) = 16cm2, find the area of ΔABC.
(ii) If DE = 4cm, BC = 8 cm and Area (ΔADE) = 25cm2, find the area of ΔABC.
(iii) If DE : BC = 3 : 5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.
Answer: In the given figure, we have DE ∥ BC.
In ΔADE and ΔABC
∠ADE = ∠B (Corresponding angles)
∠DAE = ∠BAC (Common)
So, ΔADE and ΔABC (AA Similarity)
(i) We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Hence,
Ar(ΔADE)/Ar(ΔABC) = DE2/BC2
16/Ar(ΔABC) = 42/62
Ar(ΔABC) 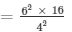
Ar(ΔABC) = 36 cm2
(ii) We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Hence,
Ar(ΔADE)/Ar(ΔABC) = DE2/BC2
25/Ar(ΔABC) = 42/82
Ar(ΔABC) = 
Ar(ΔABC) = 100 cm2
(iii) We know that
Ar(ΔADE)/Ar(ΔABC) = DE2/BC2
Ar(ΔADE)/Ar(ΔABC) = 32/52
Ar(ΔADE)/Ar(ΔABC) = 9/25
Let the area of ΔADE = 9x sq units
area of ΔABC = 25x sq units
Now, Ar(ΔADE)/Ar(trapBCED) = 9x/16x
Ar(ΔADE)/Ar(trapBCED) = 9/16
9. In ΔABC , D and E are the mid- points of AB and AC respectively. Find the ratio of the areas ΔADE and ΔABC .
Answer: Given:
In ΔABC, D and E are the midpoints of AB and AC respectively.
To find:
Ratio of the areas of ΔADE and ΔABC
It is given that D and E are the midpoints of AB and AC respectively.
Therefore, DE II BC (Converse of mid-point theorem)
Also, DE = 1/2BC
In ΔADE and ΔABC
∠ADE = ∠B(Corresponding angles)
∠DAE = ∠BAC (common)
So, ΔADE – ΔABC (AA Similarity)
We know that the ratio of areas of two similar triangles is equal to the ratio of square of their corresponding sides.
Ar(ΔADE)/Ar(ΔABC) = AD2/AB2
Ar(ΔADE)/Ar(ΔABC) = 12/22
Ar(ΔADE)/Ar(ΔABC) = 1/4
10. The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude of the bigger triangles is 5 cm, find the corresponding altitude of the other.
Answer: Given: the area of the two similar triangles is 100cm2 and 49cm2 respectively. If the altitude of the bigger triangle is 5cm
To find: their corresponding altitude of the other triangle
We know that the ratio of the areas of the two similar triangles is equal to the ratio of squares of their corresponding altitudes.
ar(biggertriangle1)/Ar(triangle2) = (altitude of the bigger triangle1/altitude2)2
(100/49) = (5/altitude2)2
Taking squares on both the sides
(10/7 = (5/altitude2)
Altitude 2 = 3.5cm
11. The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
Answer: Given : the area of the two triangles is 121cm2 and 64cm2 respectively. If the merdian of the first triangle is 12.1cm
To find the corresponding medians of the other triangle
We know that ratio of the areas of the two similar triangles are equal to the ratio of the squares of their merdians
(ar(triangle1)/ar(triangle2) = (median1/median2)2
(121/64 = (12.1/median2)2
Taking the squareroot on the both sides
(11/8 = (12.1/median2)
Median2 = 8.8cm
12. If ΔABC∼ΔDEF such that AB = 5cm, area (ΔABC) = 20 cm2 and area (ΔDEF) = 45 cm2, determine DE.
Answer:
Given : the area of the two similar ΔABC = 20cm2 and ΔDEF = 45cm2 and AB = 5cm
To measure of DE
We know that the ratio of the areas of the two similar triangles is equal to the ratio of the squares of their corresponding sides.
arΔABC/arΔDEF = (AB/DE)2
20/45 = 52/DE
20/45 = 5/DE
DE2 = 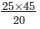
DE2 = 225/4
DE = 7.5cm
13. In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find BP/AB.
Answer: Given: in ΔABC, PQ is a line segment intersecting AB at P and AC at such that PQ∥BC and PQ divides ΔABC in two parts equal in area
To find : BP/AB
We have PQ∥BC and
Ar(ΔAPQ) = Ar(quad BPQC)
Ar(ΔAPQ) +Ar(ΔAPQ) = Ar(quad BPQC) +Ar(ΔAPQ)
2(Ar(ΔAPQ) = Ar(ΔABC)
Now PQ∥BC and BA is a transversal
In ΔABC and ΔAPQ)
∠APQ = ∠B (corresponding angles)
∠PAQ = ∠BAC (common)
In ΔABC∼ΔAPQ) (AA similarity)
We know that the ratio of the areas of the two similar triangles is used and is equal to the ratio of their squares of the corresponding sides.
Hence
ArΔAPQ/ArΔABC = (AP/AB)2
ArΔAPQ2/ArΔABC = (AP/AB)2
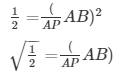
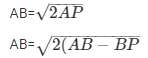
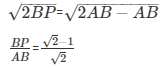
14. The areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm, find the length of QR.
Answer:Given: the areas of the two similar triangles ABC and PQR are in the ratio 9:16. BC = 4.5cm
To find: Length of QR
We know that the ratio of the areas of the two similar triangles is equal to the ratio of the squares of their corresponding sides.
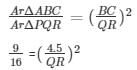
3/4 = 4.5/QR
QR = 18/3 = 6cm
15. ABC is a triangle and PQ is a straight line meeting AB and P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one – sixteenth of the area of ΔABC.
Answer: Given : in ΔABC, PQ is a line segment intersecting AB at P and AC at Q. AP = 1cm , PB = 3cm, AQ = 1.5 cm and QC = 4.5cm
To find Ar(ΔAPQ) = 1/16×ΔABC)
In ΔABC
AP/PB = AQ/QC
1/3 = 1/3
According to converse of basic proportional theorem if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Hence,
PQ∥BC
Hence in ΔABC and ΔAPQ
∠APQ = ∠B (corresponding angles)
∠PAQ = ∠BAC (common)
ΔABC∼ΔAPQ
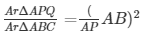

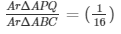
16. If D is a point on the side AB of ΔABC such that AD : DB = 3 : 2 and E is a point on BC such that DE || AC. Find the ratio of areas of ΔABC and ΔBDE.
Answer: Given In ΔABC, D is appoint on the side AB such that AD:DB = 3:2. E is a point on side BC such that DE∥AC
To find
ΔABCΔBDE
In ΔABC,ΔBDE,
∠BDE = ∠A (corresponding angles)
∠DBE = ∠ABC
ΔABC∼ΔBDE
We know that the ratio of the two similar triangles is equal to the ratio of the squares of their corresponding sides
Let AD = 2x and BD = 3x
Hence
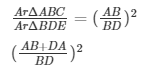
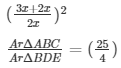
17. If ΔABC and ΔBDE are equilateral triangles, where D is the midpoint of BC, find the ratio of areas of ΔABC and ΔBDE .
Answer: Given In ΔABC, ΔBDE are equilateral triangles. D is the point of BC.
To find ArΔABC/ArΔBDE
In ΔABC, ΔBDE
ΔABC∼ΔBDE (AAA criteria of similarity all angles of the equilateral triangles are equal)
Since D is the mid point of BC, BD : DC = 1
We know that the ratio of the areas of the two similar triangles is equal to the ratio of squares of their corresponding sides.
Let DC = x, and BD = x
Hence
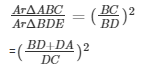

ArΔABC/ArΔBDE = 4:1
18.Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
Answer: Given:
Two isosceles triangles have equal vertical angles and their areas are in the ratio of 36: 25.
To find:
Ratio of their corresponding heights
Suppose ΔABC and ΔPQR are two isosceles triangles with ∠A = ∠P.
Therefore,
AB/AC = PQ/PR
In ΔABC and ΔPQR,
∠A = ∠P
AB/AC = PQ/PR
∴ ΔABC – ΔPQR (SAS similarity)
Let AD and PS be the altitudes of ΔABC and ΔPQR, respectively.
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
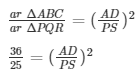
AD/PS = 6/5
Hence, the ratio of their corresponding heights is 6: 5.
19. In the given figure. ΔABC and ΔDBC are on the same base BC. If AD and BC intersect at O, Prove that
Area of(ΔABC)/Area of(ΔDBC) = AO/DO
Answer: Given ΔABC and ΔDBC are on the same BC. AD and BC intersect at O.
Prove that :ArΔABC/ArΔDBC = AO/DO
AL⊥BC and DM⊥BC
Now, in ΔALO and ΔALOwe have
∠ALO = ∠DMO = 90∘
∠AOL = ∠DOM (vertically opposite angles)
Therefore ΔALO∼ΔDMO
∴ AL/DM = AO/DO
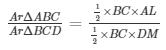
= AL/DM
= AO/DO
20. ABCD is a trapezium in which AB || CD. The Diagonal AC and BC intersect at O. Prove that :
(i) ΔAOB ΔCOD
(ii) If OA = 6 cm, OC = 8 cm,
Find:
(a) Area of(ΔAOB)/Area of(ΔCOD)
(b) Area of(ΔAOD)/Area of(ΔCOD)
Answer: Given ABCD is the trapezium which AB∥CD
The diagonals AC and BD intersect at o.
To prove:
(i) ΔAOB∼ΔCOD
(ii) If OA = 6 cm, OC = 8 cm
To find :
(a) ArΔAOB/ArΔCOD
(b) ArΔAOD/ArΔCOD
Construction : Draw a line MN passing through O and parallel to AB and CD
Now in ΔAOB and ΔCOD
(i) Now in ∠OAB = ∠OCD (Alternate angles)
(ii) ∠OBA = ∠ODC (Alternate angles)
∠AOB = ∠COD (vertically opposite angle)
ΔAOB∼ΔCOD (A.A.Acrieteria)
a) We know that the ratio of areas of two triangles is equal to the ratio of squares of their corresponding sides.
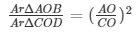
= (6/8)2

b) We know that the ratio of two similar triangles is equal to the artio of their corresponding
sides.


21. In ΔABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
Answer: Given : In ΔABC , P divides the side AB such that AP: PB = 1:2, Q is a point on AC on such that PQ ∥BC
To find : The ratio of the areas of ΔAPQ and the trapezium BPQC.
In ΔAPQ and ΔABC
∠APQ = ∠B (corresponding angles)
∠PAQ = ∠BAC (common)
So, ΔAPQ∼ΔABC (AA Similarity)
We know that the ratio of areas of the twosimilar triangles is equal to the ratio of the squares of their corresponding sides.
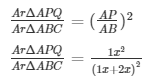
ArΔAPQ/ArΔABC = 1/9
Let Area of ΔAPQ = 1 sq. units and Area of ΔABC = 9x sq.units
Ar[trapBCED] = Ar(ΔABC ) – Ar(ΔAPQ)
= 9x-1x
= 8x sq units
Now,
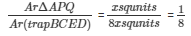
|
5 videos|292 docs|59 tests
|
FAQs on Ex-4.6 Triangles, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are some properties of triangles that can help in solving problems related to them? |  |
| 2. How can I determine if two triangles are congruent? |  |
| 3. How can I find the area of a triangle? |  |
| 4. How do I determine if a triangle is a right triangle? |  |
| 5. How can I find the length of an unknown side in a triangle? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















