Ex-5.1 Trigonometric Ratios (Part - 3), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
12.) If tanΘ = a/b, prove that 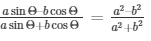
Sol.
Given:
tanΘ a/b …. (1)
Now, we know that tanΘ = sinΘ/cosΘ
Therefore equation (1) becomes
sinΘ/cosΘ = a/b ….(2)
Now, by multiplying by a/b on both sides of equation (2)
We get,
a/b × sinΘ/cosΘ = a/b × a/b
Therefore,
asinΘ/bcosΘ = a2/b2 ….(3)
Now by applying dividendo in above equation (3)
We get,
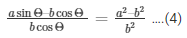
Now by applying componendo in equation (3)
We get,
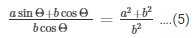
Now, by dividing equation (4) by equation (5)
We get,
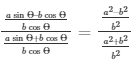
Therefore,
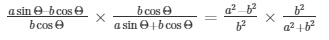
Therefore, bcosΘ and b2 cancels on L.H.S and R.H.S respectively
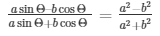
Hence, it is proved that
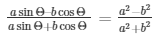
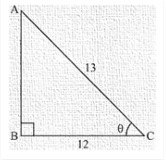
13.) If secΘ = 13/5, show that 
Sol.
Given:
secΘ = 13/5
To show that 
Now, we know that cosΘ = 1/secΘ
Therefore,
cosΘ = 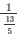
Therefore,
cosΘ = 5/13 …. (1)
Now, we know that
cosΘ = 
Now, by comparing equation (1) and(2)
We get,
Base side adjacent to ∠Θ = 5
And
Hypotenuse = 13
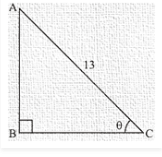
Therefore from above figure
Base side BC = 5
Hypotenuse AC = 13
Side AB is unknown. It can be determined by using Pythagoras theorem
Therefore by applying Pythagoras theorem
We get,
AC2 = AB2 + BC2
Therefore by substituting the values of known sides
We get,
132 = AB2 + 52
Therefore,
AB2 = 132 – 52
AB2 = 169 – 25
AB2 = 144
AB = 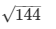
Therefore,
AB = 12 …. (3)
Now, we know that
sinΘ = AB/AC
sinΘ = 12/13 …. (4)
Now L.H.S of the equation to be proved is as follows
L.H.S = 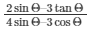
Substituting the value cosΘ of sinΘand from equation (1) and (4) respectively
We get,
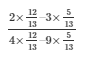
Therefore,
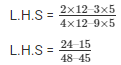
L.H.S = 9/3
L.H.S = 3
Hence proved that,
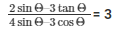
14.) If cosΘ = 12/13 , show that sinΘ(1–tanΘ) = 35/156
Sol. Given: cosΘ = 12/13 …. (1)
To show that sinΘ(1–tanΘ) = 35/156
Now we know that cosΘ = Basesideadjacentto∠Θ/Hypotenuse ….(2)
Therefore, by comparing equation (1) and (2)
We get,
Base side adjacent to ∠Θ = 12
And
Hypotenuse = 13
Therefore from above figure
Base side BC = 12
Hypotenuse AC = 13
Side AB is unknown and it can be determined by using Pythagoras theorem
Therefore by applying Pythagoras theorem
We get,
AC2 = AB2 + BC2
Therefore by substituting the values of known sides
We get,
132 = AB2 + 122
Therefore,
AB2 = 132– 122
AB2 = 169 – 144
AB = 25
AB = 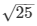
Therefore,
AB = 5 …. (3)
Now, we know that
sinΘ = Perpendicularsideoppositeto∠Θ/Hypotenuse
Now from figure (a)
We get,
sinΘ = AB/AC
Therefore,
sinΘ = 5/12 …. (5)
Now L.H.S of the equation to be proved is as follows
L.H.S of the equation to be proved is as follows
L.H.S = sinΘ(1–tanΘ] …. (6)
Substituting the value of sinΘ and tanΘ from equation (4) and (5)
We get,
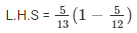
Taking L.C.M inside the bracket
We get,
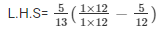
Therefore,
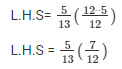
Now by opening the bracket and simplifying
We get,
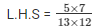
L.H.S = 35/136
From equation (6) and (7) ,it can be shown that
that sinΘ(1–tanΘ) = 35/136
15.) If cotΘ = 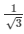 , show that
, show that 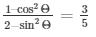
Sol. Given: cotΘ = 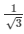 …. (1)
…. (1)
To show that 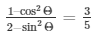
Now, we know that cotΘ = 1/tanΘ
Since tanΘ = Perpendicular side oppositeto∠Θ/Base side adjacentto∠Θ
Therefore,
tanΘ = 
Therefore,
cotΘ = Base side adjacentto∠Θ/Perpendicular side oppositeto∠Θ …. (2)
Comparing Equation (1) and (2)
We get.
Base side adjacent to ∠Θ = 1
Perpendicular side opposite to ∠Θ = √3
Therefore, triangle representing angle √3 is as shown below
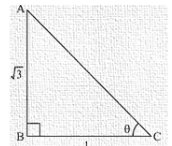
Therefore, by substituting the values of known sides
We get,
AC2 = (√3)2 + 12
Therefore,
AC2 = 3 + 1
AC2 = 4
AC = √4
Therefore,
AC = 2 …. (3)
Now, we know that
sinΘ = Perpendicular side oppositeto∠Θ/Hypotenuse
Now from figure (a)
sinΘ = AB/AC
Therefore from figure (a) and equation (3),
sinΘ = 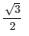
Now we know that
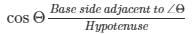
Now from figure (a)
We get,
BC/AC
Therefore from figure (a) and equation (3),
cosΘ = 1/2 …. (5)
Now, L.H.S of the equation to be proved is as follows
L.H.S = 
Substituting the value of from equation (4) and (5)
We get,
L.H.S = 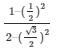
L.H.S = 
Now by taking L.C.M in numerator as well as denominator
We get,
L.H.S = 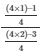
Therefore,
L.H.S = 
L.H.S = 3/4 × 4/5
L.H.S = 3/5 = R.H.S
Therefore,
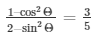
16.) If tanΘ = 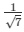 , then show that
, then show that 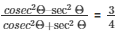
Sol. Given: tanΘ = 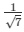 …. (1)
…. (1)
To show that 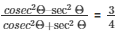
Now, we know that
Since, tanΘ = Perpendicular side oposite to∠Θ/Base side adjacent to∠Θ ….(2)
Therefore,
Comparing equation (1) and (2)
We get.
Perpendicular side opposite to ∠Θ = 1
Base side adjacent to ∠Θ = √7
Therefore, Triangle representing ∠Θ is shown below
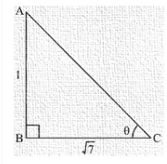
Hypotenuse AC is unknown and it can be found by using Pythagoras theorem
Therefore by applying Pythagoras theorem
We get,
AC2 = AB2 + BC2
Therefore by substituting the values of known sides
We get,
AC2 = (1)2 + (√7)2
Therefore,
AC 2 = 1 + 7
AC2 = 8
AC = √8
AC = 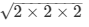
Therefore,
AC = 2√2 …. (3)
Now we know that
sinΘ = Perpendicular side opposite to∠Θ/Hypotenuse
sinΘ = AB/AC
sinΘ = 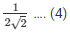
Now, we know that cosec Θ = 1/sinΘ
Therefore, from equation (4)
We get,
cosec Θ = 2√2 …. (5)
Now, we know that
cosΘ = Base side adjacent to∠Θ/Hypotenuse
Now from figure (a)
We get,
cosΘ = BC/AC
Therefore from figure (a) and equation (3)
cosΘ = 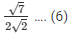
Now we know that secΘ = 1/cosΘ
Therefore, from equation (6)
We get,
secΘ = 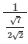
secΘ = 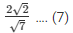
Now, L.H.S of the equation to be proved is as follows
L.H.S = 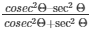
Substituting the value of cosecΘ andsecΘ from equation (6) and (7)
We get,
L.H.S = 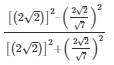
L.H.S = 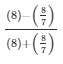
Therefore,
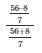
L.H.S = 
Therefore,
L.H.S = 48/64
L.H.S = 3/4 = R.H.S
Therefore,
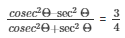
Hence proved that
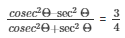
17.) If secΘ = 5/4,find the value of 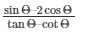
Sol. Given: secΘ = 5/4 …. (1)
To find the value of 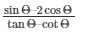
Now we know that secΘ = 1/cosΘ
Therefore,
cosΘ = 1/secΘ
Therefore from equation (1)
cosΘ = 1/5
cosΘ = 4/5 …. (2)
Also, we know that cos2Θ + sin2Θ = 1
Therefore,
sin2Θ = 1–cos2Θ
sinΘ = 
Substituting the value of cosΘ from equation (2)
We get,
sinΘ = 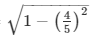
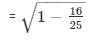
= 9/25
= 3/5
Therefore,
sinΘ = 3/5 …. (3)
Also, we know that
sec2Θ = 1 + tan2Θ
Therefore,
tan2Θ = (5/4)2 −1
tanΘ = 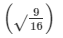
Therefore,
tanΘ = 3/4 …. (4)
Also, cotΘ = 1/tanΘ
Therefore from equation (4)
We get,
cotΘ = 4/3 …. (5)
Substituting the value of cosΘ, cotΘ and tanΘ from the equation (2),(3),(4) and (5) respectively in the expression below
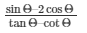
We get,
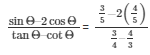
= 12/7
Therefore, 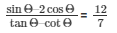
18.) If sinΘ = 12/13 , find the value of 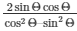
Sol. Given: sinΘ = 12/13 …. (1)
To, find the value of 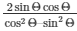
Now, we know the following trigonometric identity
cosec2 Θ = 1 + tan2Θ
Therefore, by substituting the value of tanΘ from equation (1)
We get,
cosec2 Θ = 1 + (12/13)2
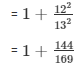
By taking L.C.M on the R.H.S
We get,
cosec2Θ =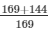
= 313/169
Therefore
cosecΘ = 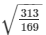
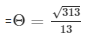
Therefore
cosecΘ = Θ =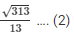
Now, we know that
cosecΘ = 1/sinΘ
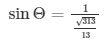
Therefore

Now, we know the following trigonometric identity
cos2Θ + sin2Θ = 1
Therefore,
cos2Θ = 1–sin2Θ
Now by substituting the value of sinΘ from equation (3)
We get,
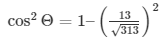
= 1–169/313
Therefore, by taking L.C.M on R.H.S
We get,
cos2Θ = 144/313
Now, by taking square root on both sides
We get,
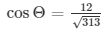
Therefore,
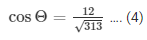
Substituting the value of sinΘ and cosΘ from equation (3) and (4) respectively in the equation below
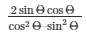
Therefore,
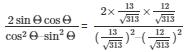
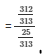 312/25
312/25
Therefore
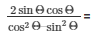 312/25
312/25
19.) If cosΘ = 3/5 , find the value of 
Sol.
Given: cosΘ = 3/5 …. (1)
To find the value of 
Now we know the following trigonometric identity
cos2Θ + sin2Θ = 1
Therefore by substituting the value of cosΘ from equation (1)
We get,
(3/5)2 + sin2Θ = 1
Therefore,
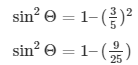
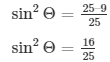
Therefore by taking square root on both sides
We get,
sinΘ = 4/5 …. (2)
Now, we know that
tanΘ = sinΘ/cosΘ
Therefore by substituting the value of sinΘ and cosΘ from equation (2) and (1) respectively
We get,
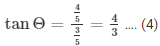
Now, by substituting the value of sinΘ and of tanΘ from equation (2) and equation (4) respectively in the expression below
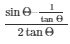
We get,
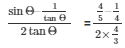
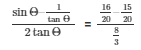

Therefore,
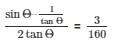
20.) If sinΘ = 35 , find the value of 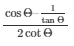
Sol. Given:
sinΘ = 3/5 …. (1)
To find the value of 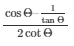
Now, we know the following trigonometric identity
cos2Θ + sin2Θ = 1
Therefore by substituting the value of cosΘ from equation (1)
We get,
cos2Θ + (3/5)2 = 1
Therefore,
cos2Θ = 1–(3/5)2
cos2Θ = 1–9/25
Now by taking L.C.M
We get,
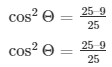
Therefore, by taking square roots on both sides
We get,
cosΘ = 4/5
Therefore,
cosΘ = 4/5 …. (2)
Now we know that
tanΘ = sinΘ/cosΘ
Therefore by substituting the value of sinΘ and cosΘ from equation (1) and (2) respectively
We get,

tanΘ = 3/4 …. (3)
Also, we know that
cotΘ = 1/tanΘ
Therefore from equation (3)
We get,
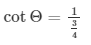
cotΘ = 4/3 …. (4)
Now by substituting the value of cosΘ, tanΘ and cotΘ from equation (2) ,(3) and (4) respectively from the expression below
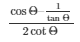
We get,
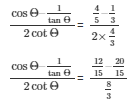
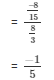
Therefore, 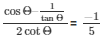
21.) If tanΘ = 24/7, find that sinΘ + cosΘ
Sol.
Given:
tanΘ = 24/7 …. (1)
To find,
sinΘ + cosΘ
Now we know that tanΘ is defined as follows
tanΘ = Perpendicular side opposite to∠Θ/Base side adjacentto∠Θ …. (2)
Now by comparing equation (1) and (2)
We get,
Perpendicular side opposite to ∠Θ = 24
Base side adjacent to ∠Θ = 7
Therefore triangle representing ∠Θ is as shown below
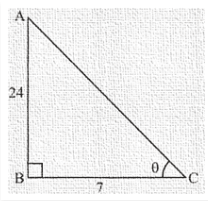
Side AC is unknown and can be found by using Pythagoras theorem
Therefore,
AC2 = AB2 + BC2
Now by substituting the value of unknown sides from figure
We get,
AC2 = 242 + 72
AC = 576 + 49
AC = 625
Now by taking square root on both sides,
We get,
AC = 25
Therefore H hy
Hypotenuse side AC = 25 …. (3)
Now we know sinΘ is defined as follows
sinΘ = Perpendicular side opposite to∠Θ/Hypotenuse
Therefore from figure (a) and equation (3)
We get,
sinΘ = AB/AC
sinΘ = 24/25 …. (4)
Now we know that cosΘ is defined as follows
cosΘ = Base side adjacent to∠Θ/Hypotenuse
Therefore by substituting the value of sinΘ and cosΘ from equation (4) and (5) respectively, we get
sinΘ + cosΘ = 24/25 + 7/25
sinΘ + cosΘ = 31/25
Hence, sinΘ + cosΘ = 31/25
22.) If sinΘ = a/b, find secΘ + tanΘ in terms of a and b.
Sol. Given:
sinΘ = a/b …. (1)
To find: secΘ + tanΘ
Now we know, sinΘ is defined as follows
sinΘ = Perpendicularsideoppositeto∠ΘHypotenuse …. (2)
Now by comparing equation (1) and (2)
We get,
Perpendicular side opposite to ∠Θ = a
Hypotenuse = b
Therefore triangle representing ∠Θ is as shown below

Hence side BC is unknown
Now we find BC by applying Pythagoras theorem to right angled ΔABC
Therefore,
AC2 = AB2 + BC2
Now by substituting the value of sides AB and AC from figure (a)
We get,
b2 = a2 + BC2
Therefore,
BC2 = b2 – a2
Now by taking square root on both sides
We get,

Therefore,
Base side  …. (3)
…. (3)
Now we know cosΘ is defined as follows
cosΘ = Base side adjacent to∠Θ/Hypotenuse
Therefore from figure (a) and equation (3)
We get,
cosΘ = BC/AC
= 
cosΘ = BC/AC
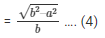
Now we know, secΘ = 1/cosΘ
Therefore,
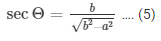
Now we know, tanΘ = sinΘ/cosΘ
Now by substituting the values from equation (1) and (3)
We get,
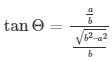
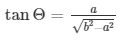
Therefore,
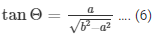
Now we need to find secΘ + tanΘ
Now by substituting the values of secΘ and tanΘ from equation (5) and (6) respectively
We get,
secΘ + tanΘ = 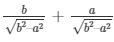
secΘ + tanΘ = 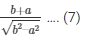
We get,
secΘ + tanΘ = 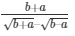
Now by substituting the value in above expression
We get,
secΘ + tanΘ =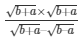
Now, 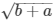 present in the numerator as well as denominator of above denominator of above expression gets cancels we get,
present in the numerator as well as denominator of above denominator of above expression gets cancels we get,
secΘ + tanΘ = 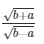
Square root is present in the numerator as well as denominator of above expression
Therefore we can place both numerator and denominator under a common square root sign
Therefore, secΘ + tanΘ = 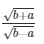
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















