Ex-5.2 Trigonometric Ratios (Part - 1), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Evaluate each of the following:
Q 1 . sin 45° sin 30° + cos 45° cos 30°
Solution:
Sin 45°sin 30° + cos 45° cos 30° [1]
We know that by trigonometric ratios we have ,
sin45° = 1/√2 sin30° = 1/2
cos45° = 1/√2 cos30° = √3/2
Substituting the values in equation 1 , we get
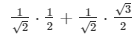
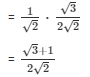
Q 2 . sin 60° cos 30° + cos 60° sin 30°
Solution:
sin 60° cos 30° + cos 60° sin 30° [1]
By trigonometric ratios we have ,
sin60° = √3/2 sin30° = 1/2
cos30° = √3/2 cos60° = 1/2
Substituting the values in equation 1 , we get
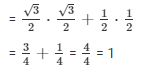
Q 3 . cos 60° cos 45° – sin 60° sin 45°
Solution:
cos 60° cos 45° – sin 60° sin 45° [1]
We know that by trigonometric ratios we have ,
cos60° = 1/2 cos45° = 1/√2
sin60° = √3/2 sin45° = 1/√2
Substituting the values in equation 1 , we get
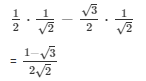
Q.4: sin230° + sin245° + sin260° + sin290°
Solution:
sin230° + sin245° + sin260° + sin290° [1]
We know that by trigonometric ratios we have ,
sin30° = 1/2 sin45° = 1/√2
sin60° = √3/2 sin90° = 1
Substituting the values in equation 1 , we get
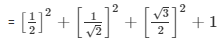
= 1/4 + 1/2 + 3/4 + 1
= 5/2
Q 5. cos230° + cos245° + cos260° + cos290°
Solution:
cos230° + cos245° + cos260° + cos290° [1]
We know that by trigonometric ratios we have ,
cos30° = √3/2 cos45° = 1/√2
cos60° = 1/2 cos90° = 0
Substituting the values in equation 1 , we get
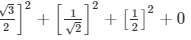
= 3/4 + 1/2 + 1/4
= 3/2
Q 6 . tan230° + tan245° + tan260°
Solution:
tan230° + tan245° + tan260° [1]
We know that by trigonometric ratios we have ,
tan30° = 1/√3 tan60° = √3
tan45° = 1
Substituting the values in equation 1 , we get
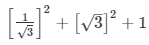
= 1/3 + 3 + 1
= 13/3
Q 7 . 2sin230° − 3cos245° + tan260°
Solution:
2sin230° − 3cos245° + tan260° [1]
We know that by trigonometric ratios we have ,
sin30° = 1/2 cos45° = 1/√2
tan60° = √3
Substituting the values in equation 1 , we get
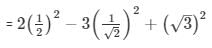
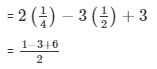
= 2
Q8:sin230°cos245° + 4tan230° + 1/2sin290° − 2cos290° + 1/24cos20°
Solution:
sin230°cos245° + 4tan230° + 1/2sin290° − 2cos290° + 1/24cos20° [1]
We know that by trigonometric ratios we have ,
sin30° = 1/2
cos45° = 1/√2
tan30° = 1/√3
sin90° = 1
cos90° = 0
cos0° = 1
Substituting the values in equation 1 , we get
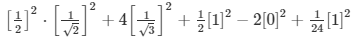
= 1/8 + 4/3 + 1/2 + 1/24
= 48/24 = 2
Q 9 . 4(sin460° + cos430°) − 3(tan260° − tan245°) + 5cos245°
Solution:
4(sin460° + cos430°) − 3(tan260° − tan245°) + 5cos245° [1]
We know that by trigonometric ratios we have ,
sin60° = √3/2 cos45° = 1/√2
tan60° = √3 cos30° = √3/2
Substituting the values in equation 1 , we get
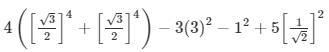
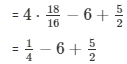
= 14/2 − 6 = 7 – 6 = 1
Q 10 . (cosec245°sec230°)(sin230° + 4cot245° − sec260°)
Solution:
(cosec245°sec230°)(sin230° + 4cot245° − sec260°) [1]
We know that by trigonometric ratios we have ,
cosec45° = √2 sec30° = 2/√3
sin30° = 1/2 cot45° = 1
sec60° = 2
Substituting the values in equation 1 , we get
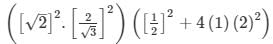
= 3⋅4/3⋅1/4
= 2/3
Q11. cosec330°cos60°tan345°sin290°sec245°cot30°
Solution:
Given,
= cosec330°cos60°tan345°sin290°sec245°cot30°
= 23(1/2)(13)(12)(√22)(√3)
= (2)3×(1/2)×(13)×(12)×(√22)×(√3)
= 8×(1/2)×(1)×(1)×(2)×(√3)
= 8√3
Q12. cot230° − 2cos260° − 3/4sec245° – 4sec230°
Solution:
Given,
= cot230° − 2cos260° − 34sec245° – 4sec230°
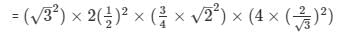
= 3 − 1/2 − 3/2 − 16/3
= − 13/3
Q13. (cos0° + sin45° + sin30°)(sin90° − cos45° + cos60°)
Solution:
Given,
(cos0° + sin45° + sin30°)(sin90° − cos45° + cos60°)
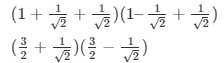
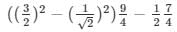
Q14. 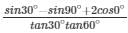
Solution:
Given,
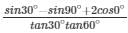
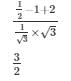
Q15. 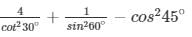
Solution:
Given,
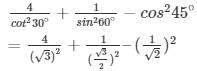
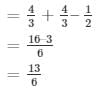
Q16. 4(sin430° + cos260°) − 3(cos245° − sin290°) − sin260°
Solution:
Given,
4(sin430° + cos260°) − 3(cos245° − sin290°) − sin260°
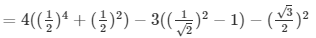
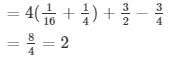
Q17.
Solution:
Given,

= 3 + 2 + 4 = 9
Q18. 
Solution:
Given,
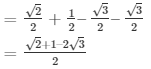
Q19. 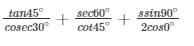
Solution:
Given,
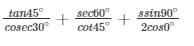
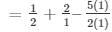
= 5/2 – 5/2 = 0
Q20. 2sin3x = √3
Solution:
Given,
2sin3x = √3
⇒ sin3x = √3/2
⇒ sin3x = sin60°
⇒ 3x = 60°
⇒ x = 20°
Q21) 2sinx/2 = 1,x = ?
Solution:
sinx/2 = 1/2
sinx/2 = sin30°
x/2 = 30°
x = 60°
Q22) √3sinx = cosx
Solution:
√3tanx = 1
tanx = 1/√3
∴tanx = tan45°
x = 45°
Q23) Tan x = sin 45° cos 45° + sin 30°
Solution:
Tanx = 1/√2.12√ + 1/2 [∵sin45° = 1/√2cos45° = 1/√2sin30° = 1/2]
Tanx = 1/2 + 1/2
Tan x = 1
Tan x = 45°
x = 45°
Q24) √3Tan2x = cos60° + sin45°cos45°
Solution:
√3Tan2x = 1/2 +1/√2.1/√2 [∵cos60° = 12sin45° = cos45° = 1/√2]
√3Tan2x = 1√3 ⇒ tan2x = tan30°
2x = 30°
x = 150
Q25) cos2x = cos60°cos30° + sin60°sin30°
Solution:
cos2x = 1/2.3√2 + √3/2.1/2 [∵cos60° = sin30° = 1/2sin60° = cos30° = √3/2]
cos2x = 2.3√4
cos2x = √3/2
cos2x = cos30°
2x = 30°
x = 150
|
5 videos|292 docs|59 tests
|
FAQs on Ex-5.2 Trigonometric Ratios (Part - 1), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are the basic trigonometric ratios? |  |
| 2. How are sine, cosine, and tangent related to the sides of a right-angled triangle? |  |
| 3. How can trigonometric ratios be used to find missing sides in a right-angled triangle? |  |
| 4. Can trigonometric ratios be used for angles other than those in a right-angled triangle? |  |
| 5. How are trigonometric ratios useful in real-life applications? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















