Ex-8.13 Quadratic Equations, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1: Find the roots of the equation (x – 4) (x + 2) = 0
Sol:
The given equation is (x – 4) (x + 2) = 0
Either x – 4 = 0 therefore x = 4
Or, x + 2 = 0 therefore x = - 2
The roots of the above mentioned quadratic equation are 4 and - 2 respectively.
Question 2: Find the roots of the equation (2x + 3) (3x – 7) = 0
Sol:
The given equation is (2x + 3) (3x – 7) = 0.
Either 2x + 3 = 0, therefore x = −3/2
Or, 3x - 7 = 0, therefore x = 7/3
The roots of the above mentioned quadratic equation are x = −3/2 and x = 7/3 respectively.
Question 3: Find the roots of the quadratic equation 3x2 - 14x - 5 = 0
Sol:
The given equation is 3x2 - 14x - 5 = 0
= 3x2 - 14x - 5 = 0
= 3x2 - 15x + x - 5 = 0
= 3x(x - 5) + 1(x - 5) = 0
= (3x + 1)(x - 5) = 0
Either 3x + 1 = 0 therefore x = −1/3
Or, x - 5 = 0 therefore x = 5
The roots of the given quadratic equation are 5 and x = −1/3 respectively.
Question 4: Find the roots of the equation 9x2 - 3x - 2 = 0.
Sol:
The given equation is 9x2 - 3x - 2 = 0.
= 9x2 - 3x - 2 = 0.
= 9x2 - 6x + 3x - 2 = 0
= 3x (3x - 2) + 1(3x - 2) = 0
= (3x - 2)(3x + 1) = 0
Either, 3x - 2 = 0 therefore x = 2/3
Or, 3x + 1 = 0 therefore x = −1/3
The roots of the above mentioned quadratic equation are x = 2/3 and x = −1/3 respectively.
Question 5: Find the roots of the quadratic equation 
Sol:
The given equation is 


Cancelling out the like terms on both the sides of the numerator. We get,

= x2 + 4x - 5 = 7
= x2 + 4x - 12 = 0
= x2 + 6x - 2x - 12 = 0
= x(x + 6) - 2(x - 6) = 0
= (x + 6)(x - 2) = 0
Either x + 6 = 0
Therefore x = - 6
Or, x - 2 = 0
Therefore x = 2
The roots of the above mentioned quadratic equation are 2 and - 6 respectively.
Question 6: Find the roots of the equation 6x2 + 11x + 3 = 0.
Sol:
The given equation is 6x2 + 11x + 3 = 0.
= 6x2 + 11x + 3 = 0.
= 6x2 + 9x + 2x + 3 = 0
= 3x(2x + 3) + 1(2x + 3) = 0
= (2x + 3)(3x + 1) = 0
Either, 2x + 3 = 0 therefore x = −3/2
Or, 3x + 1 = 0 therefore x = −1/3
The roots of the above mentioned quadratic equation are x = −3/2 and x = −1/3 respectively .
Question 7: Find the roots of the equation 5x2 - 3x - 2 = 0
Sol:
The given equation is 5x2 - 3x - 2 = 0.
= 5x2 - 3x - 2 = 0.
= 5x2 - 5x + 2x - 2 = 0
= 5x(x - 1) + 2(x - 1) = 0
= (5x + 2) (x - 1) = 0
Either 5x + 2 = 0 therefore x = −2/5
Or, x - 1 = 0 therefore x = 1
The roots of the above mentioned quadratic equation are 1 and x = −2/5 respectively.
Question 8: Find the roots of the equation 48x2 - 13x - 1 = 0
Sol:
The given equation is 48x2 - 13x - 1 = 0.
= 48x2 - 13x - 1 = 0.
= 48x2 - 16x + 3x - 1 = 0.
= 16x (3x - 1) + 1(3x - 1) = 0
= (16x + 1)(3x - 1) = 0
Either 16x + 1 = 0 therefore x = −1/16
Or, 3x - 1 = 0 therefore x = 1/3
The roots of the above mentioned quadratic equation are x = −1/16
And x = 1/3 respectively.
Question 9: Find the roots of the equation 3x2 = - 11x - 10
Sol:
The given equation is 3x2 = - 11x - 10
= 3x2 = - 11x - 10
= 3x2 + 11x + 10 = 0
= 3x2 + 6x + 5x + 10 = 0
= 3x(x + 2) + 5(x + 2) = 0
= (3x + 2)(x + 2) = 0
Either 3x + 2 = 0 therefore x = −2/3
Or, x + 2 = 0 therefore x = - 2
The roots of the above mentioned quadratic equation are x = −2/3 and - 2 respectively.
Question 10: Find the roots of the equation 25x(x + 1) = - 4
Sol:
The given equation is 25x(x + 1) = 4
= 25x(x + 1) = - 4
= 25x2 + 25x + 4 = 0
= 25x2 + 20x + 5x + 4 = 0
= 5x (5x + 4) + 1(5x + 4) = 0
= (5x + 4)(5x + 1) = 0
Either 5x + 4 = 0 therefore x = −4/5
Or, 5x + 1 = 0 therefore x = −1/5
The roots of the quadratic equation are x = −4/5 and x = −1/5 respectively.
Question 12: Find the roots of the quadratic equation 1/x− = 3
= 3
Sol:
The given equation is 1/x− = 3
= 3
= 1/x− = 3
= 3

Cross multiplying both the sides. We get,
= 2 = 3x(x - 2)
= 2 = 3x2 - 6x
= 3x2 - 6x - 2 = 0
= 3x2 - 3x - 3x - 2 = 0
= 3x2−(3 + √3)x−(3−√3)x + [(√32)−12]
= 3x2−(3 + √3)x−(3−√3)x + [(√32)−12][(√32)−12]
= √32x2−√3(√3 + 1)x−√3(√3−1)x + (√3 + 1)(√3−1)
= √3x(√3 + 1)x−(√3x−(√3 + 1))(√3−1)
= (√3x−√3−1)(√3x−√3 + 1)(√3−1)
Either = 
Therefore x = 
Or, (√3x−√3 + 1)(√3−1)
Therefore, x = 
The roots of the above mentioned quadratic equation are x =  and x =
and x =  respectively.
respectively.
Question 13: Find the roots of the quadratic equation x−1/x = 3
Sol:
The given equation is x−1/x = 3
= x−1/x = 3

= x2 - 1 = 3x
= x2 - 1 - 3x = 0






Either 
Therefore 

Therefore 
The roots of the above mentioned quadratic equation are  and
and  respectively.
respectively.
Question 14: Find the roots of the quadratic equation 
Sol:
The given equation is 


Cancelling out the like numbers on both the sides of the equation

= x2 - 3x - 28 = - 30
= x2 - 3x - 2 = 0
= x2 - 2x - x - 2 = 0
= x(x - 2) - 1(x - 2) = 0
= (x - 2)(x - 1) = 0
Either x - 2 = 0
Therefore x = 2
Or, x - 1 = 0
Therefore x = 1
The roots of the above mentioned quadratic equation are 1 and 2 respectively.
Question 15: Find the roots of the quadratic equation a2x2 - 3abx + 2b2 = 0
Sol:
The given equation is a2x2 - 3abx + 2b2 = 0
= a2x2 - 3abx + 2b2 = 0
= a2x2 - abx - 2abx + 2b2 = 0
= ax(ax - b) - 2b(ax - b) = 0
= (ax - b)(ax - 2b) = 0
Either ax - b = 0 therefore x = b/a
Or, ax - 2b = 0 therefore x = 2b/a
The roots of the quadratic equation are x = 2b/a and x = b/a respectively.
Question 16: Find the roots of the 4x2 + 4bx - (a2 - b2) = 0
Sol:
- 4(a2 - b2) = - 4(a - b)(a + b)
= - 2(a - b) * 2(a + b)
= 2(b - a) * 2(b + a)
= 4x2 + (2(b - a) + 2(b + a)) – (a - b)(a + b) = 0
= 4x2 + 2(b - a)x + + 2(b + a)x + (b - a)(a + b) = 0
= 2x(2x + (b - a)) + (a + b)(2x + (b - a)) = 0
= (2x + (b - a))(2x + b + a) = 0
Either, (2x + (b - a)) = 0
Therefore x = 
Or, (2x + b + a) = 0
Therefore x =
The roots of the above mentioned quadratic equation are x =  and x =
and x =  respectively.
respectively.
Question 17: Find the roots of the equation ax2 + (4a2 - 3b)x - 12ab = 0
Sol:
The given equation is ax2 + (4a2 - 3b)x - 12ab = 0
= ax2 + (4a2 - 3b)x - 12ab = 0
= ax2 + 4a2x - 3bx - 12ab = 0
= ax(x - 4a) – 3b(x - 4a) = 0
= (x - 4a)(ax - 4b) = 0
Either x - 4a = 0
Therefore x = 4a
Or, ax - 4b = 0
Therefore x = 4ba
The roots of the above mentioned quadratic equation are x = 4b/a and 4a respectively.
Question 18: Find the roots of 
Sol:
The given equation is 
= = (x + 3)(2x - 3) = (x + 2){3x - 7)
= 2x2 - 3x + 6x - 9 = 3x2 - x - 14
= 2x2 + 3x - 9 = 3x2 - x - 14
= x2 - 3x - x - 14 + 9 = 0
= x2 - 5x + x - 5 = 0
= x(x - 5) + 1(x - 5) = 0
= (x - 5) (x + l) - 0
Either x - 5 - 0 or x + 1 = 0
x = 5 and x = - 1
The roots of the above mentioned quadratic equation are 5 and - 1 respectively.
Question 19: Find the roots of the equation 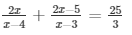
Sol:
The given equation is 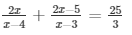
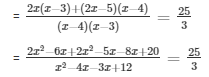

= 3(4x2 - 19x + 20) = 25(x2 - 7x + 12)
= 12x2 - 57x + 60 = 25x2 – 175x + 300
= 13x2 - 78x - 40x + 240 = 0
= 13x2 - 118x + 240 = 0
= 13x2 - 78x - 40x + 240 = 0
= 13x(x - 6) - 40(x - 6) = 0
= (x - 6)(13x - 40) = 0
Either x - 6 = 0 therefore x = 6
Or , 13x - 40 = 0 therefore x = 40/13
The roots of the above mentioned quadratic equation are 6 and 40/13 respectively.
Question 20: Find the roots of the quadratic equation 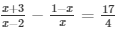
Sol:
The given equation is 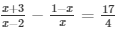

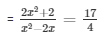
= 4(2x2 + 2) = 17(x2 - 2x)
= 8x2 + 8 = 17x2 - 34x
= 9x2 - 34x - 8 = 0
= 9x2 - 36x + 2x - 8 = 0
= 9x(x - 4) + 2(x - 4) = 0
= (9x + 2)(x - 4) = 0
Either 9x + 2 = 0 therefore x = −2/9
Or, x - 4 = 0 therefore x = 4
The roots of the above mentioned quadratic equation are x = −2/9 and 4 respectively.
Question 21: Find the roots of the quadratic equation 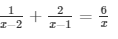
Sol:
The equation is 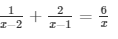
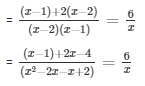

= x(3x - 5) = 6(x2 - 3x + 2)
= 3x2 - 5x = 6x2 - 18x + 12
= 3x2 - 13x + 12 = 0
= 3x2 - 9x - 4x + 12 = 0
= 3x(x - 3) - 4(x - 3) = 0
= (x - 3)(3x - 4) = 0
Either x - 3 = 0 therefore x = 3
Or, 3x - 4 = 0 therefore 4/3
The roots of the above mentioned quadratic equation are 3 and 4/3 respectively.
Question 22: Find the roots of the quadratic equation 
Sol:
The equation is 
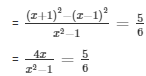
= 6(4x) = 5(x2 - 1)
= 24x = 5x2 - 5
= 5x2 - 24x - 5 = 0
= 5x2 - 25x + x - 5 = 0
= 5x(x - 5) + 1(x - 5) = 0
= (5x + 1)(x - 5) = 0
Either x - 5 = 0
Therefore x = 5
Or, 5x + 1 = 0
Therefore x = −1/5
The roots of the above mentioned quadratic equation are x = −1/5 and 5 respectively.
Question 23: Find the roots of the quadratic equation 
Sol:
The equation is 
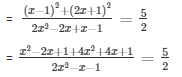
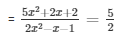
= 2(5x2 + 2x + 2) = 5(2x2 - x - 1)
= 10x2 + 4x + 4 = 10x2 - 5x - 5
Cancelling out the equal terms on both sides of the equation. We get,
= 4x + 5x + 4 + 5 = 0
= 9x + 9 = 0
= 9x = - 9
X = - 1
X = - 1 is the only root of the given equation.
Question 24: Find the roots of the quadratic equation 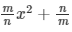 = 1−2x
= 1−2x
The given equation is 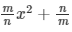 = 1−2x
= 1−2x
= 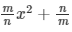 = 1−2x
= 1−2x
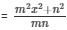 = 1−2x
= 1−2x
= m2x2 + 2mnx + (n2 - mn) = 0
Now we solve the above quadratic equation using factorization method
Therefore
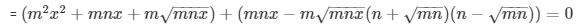
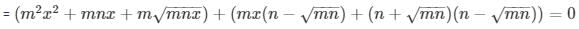
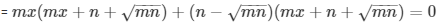

Now, one of the products must be equal to zero for the whole product to be zero for the whole product to be zero. Hence, we equate both the products to zero in order to find the value of x .
Therefore,
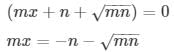
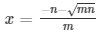
Or

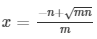
The roots of the above mentioned quadratic equation are  respectively.
respectively.
Question 25: Find the roots of the quadratic equation 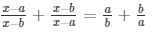
Sol:
The given equation is 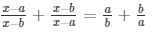
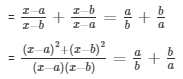

= (2x2 - 2x(a + b) + a2 + b2)ab = (a2 + b2)(x2 - (a + b)x + ab)
= (2abx2 - 2abx(a + b) + ab(a2 + b2)) = (a2 + b2)(x2 - (a2 + b2)(a + b)x + (a2 + b2)(ab)
= (a2 + b2 - 2ab)x - (a + b)(a2 + b2 - 2ab)x = 0
= (a - b)2x2 - (a + b)(a + b)2x2 = 0
= x(a - b)2(x - (a + b)) = 0
= x(x - (a + b)) = 0
Either x = 0
Or, (x - (a + b)) = 0
Therefore x = a + b
The roots of the above mentioned quadratic equation are 0 and a + b respectively.
Question 26: Find the roots of the quadratic equation 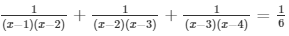
Sol:
The given equation is 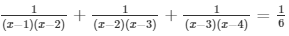


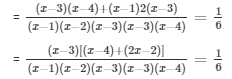
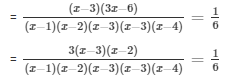
Cancelling out the like terms on both the sides of numerator and denominator. We get,
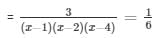
= (x - 1)(x - 4) = 18
= x2 - 4x - x + 4 = 18
= x2 - 5x - 14 = 0
= x2 - 7x + 2x - 14 = 0
= x(x - 7) + 2(x - 7) = 0
= (x - 7)(x + 2) = 0
Either x - 7 = 0
Therefore x = 7
Or, x + 2 = 0
Therefore x = - 2
The roots of the above mentioned quadratic equation are 7 and - 2 respectively.
Question 27: Find the roots of the quadratic equation 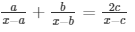
Sol:
The given equation is 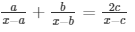

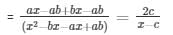
= (x - c)(ax - 2ab + bx) = 2c(x2 - bx - ax + ab)
= (a + b)x2 - 2abx - (a + b)cx + 2abc = 2cx2 - 2c(a + b)x + 2abc
Question 28: Find the roots of the Question x2 + 2ab = (2a + b)x
Sol:
The given equation is x2 + 2ab = (2a + b)x
= x2 + 2ab = (2a + b)x
= x2 - (2a + b)x + 2ab = 0
= x2 - 2ax - bx + 2ab = 0
= x(x - 2a) - b(x - 2a) = 0
= (x - 2a)(x - b) = 0
Either x - 2a = 0
Therefore x = 2a
Or, x - b = 0
Therefore x = b
The roots of the above mentioned quadratic equation are 2a and b respectively.
Question 29: Find the roots of the quadratic equation (a + b)2x2 - 4abx - (a - b)2 = 0
Sol:
The given equation is (a + b)2x2 - 4abx - (a - b)2 = 0
= (a + b)2x2 - 4abx - (a - b)2 = 0
= (a + b)2x2 - ((a + b)2 –(a - b)2 )x - (a - b)2 = 0
= (a + b)2x2 - (a + b)2 x + (a - b)2 x - (a - b)2 = 0
= (a + b)2x(x - 1) (a + b)2 (x - 1) = 0
= (x - 1) (a + b)2x + (a + b)2) = 0
Either x - 1 = 0
Therefore x = 1
Or, (a + b)2x + (a + b)2) = 0
Therefore 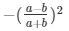
The roots of the above mentioned quadratic equation are 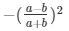 and 1 respectively .
and 1 respectively .
Question 30: Find the roots of the quadratic equation a(x2 + 1) - x(a2 + 1) = 0
Sol:
The given equation is a(x2 + 1) - x(a2 + 1) = 0
= a(x2 + 1) - x(a2 + 1) = 0
= ax2 + a - a2x - x = 0
= ax(x - a) - 1(x - a) = 0
= (x - a)(ax - 1) = 0
Either x - a = 0
Therefore x = a
Or, ax - 1 = 0
Therefore x = 1/a
The roots of the above mentioned quadratic equation are ( a) and x = 1/a respectively.
Question 31: Find the roots of the quadratic equation x2 + (a + 1/a)x + 1 = 0.
Sol:
The given equation is x2 + (a + 1/a)x + 1 = 0
= x2 + (a + 1/a)x + 1 = 0
= x2 + ax + x/a + (a×1/a) = 0
= x(x + a) + 1/a(x + a) = 0
= (x + a)(x + 1/a) = 0
Either x + a = 0
Therefore x = - a
Or , (x + 1/a) = 0
Therefore x = 1/a
The roots of the above mentioned quadratic equation are x = 1/a and –a respectively.
Question 32: Find the roots of the quadratic equation abx2 + (b2 - ac)x - bc = 0
Sol:
The given equation is abx2 + (b2 - ac)x - bc = 0
= abx2 + (b2 - ac)x - bc = 0
= abx2 + b2x - acx - bc = 0
= bx (ax + b) - c (ax + b) = 0
= (ax + b)(bx - c) = 0
Either, ax + b = 0
Therefore x = −b/a
Or, bx - c = 0
Therefore x = c/b
The roots of the above mentioned quadratic equation are x = c/b and x = −b/a respectively.
Question 33: Find the roots of the quadratic equation a2b2x2 + b2x - a2x - 1 = 0
Sol:
The given equation is a2b2x2 + b2x - a2x - 1 = 0
= a2b2x2 + b2x - a2x - 1 = 0
= b2x(a2x + 1) - 1(a2x + 1)
= (a2x + 1)( b2x - 1) = 0
Either (a2x + 1) = 0
Therefore x = 
Or, ( b2x - 1) = 0
Therefore x = 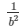
The roots of the above mentioned quadratic equation are x = 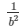 and x =
and x =  respectively.
respectively.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-8.13 Quadratic Equations, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are the different methods to solve quadratic equations? |  |
| 2. How can I determine the nature of roots of a quadratic equation? |  |
| 3. Can a quadratic equation have more than two solutions? |  |
| 4. How can I find the roots of a quadratic equation if it cannot be factorized? |  |
| 5. Can a quadratic equation have complex roots? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















