Exercise 1.3 & 1.4 - Real Numbers RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Exercise: 1.3
Question: 1
Express each of the following integers as a product of its prime.
1. 420
2. 468
3. 945
4. 7325
Solution:
To express: each of the following numbers as a product of their prime factors
1. 420
420 = 2 × 2 × 3 × 5 × 7
2. 468
468 = 2 × 2 × 3 × 3 × 13
3. 945
945 = 3 × 3 × 3 × 5 × 7
4. 7325
7325 = 5 × 5 × 293
Question: 2
Determine the prime factorization of each of the following positive integer:
1. 20570
2. 58500
3. 45470971
Solution:
To Express: Each of the following numbers as a product of their prime factors.
1. 20570
20570 = 2 × 5 × 11 × 11 × 17
2. 58500
58500 = 2 × 2 × 3 × 3 × 5 × 5 × 5 × 13
3. 45470971
45470971 = 7 × 7 × 13 × 13 × 17 × 17 × 19
Question: 3
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
Why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
We can see that both the numbers have common factor 7 and 1.
7 × 11 × 13 + 13 = (77 + 1) × 13 = 78 × 13
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = (7 × 6 × 4 × 3 × 2 + 1) × 5 = 1008 × 5
And we know that composite numbers are those numbers which have at least one more factor other than 1.
Hence after simplification we see that both numbers are even and therefore the given two numbers are composite numbers
Question: 4
Check whether 6n can end with the digit 0 for any natural number n.
Solution:
To Check: Whether 6n can end with the digit 0 for any natural number n.
We know that 6n = (2 × 3)n
6n = 2n × 3n
Therefore, prime factorization of 6n does not contain 5 and 2 as a factor together. Hence 6n can never end with the digit 0 for any natural number n.
Exercise - 1.4
Question: 1
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the integers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
To Find: LCM and HCF of following pairs of integers
To Verify: L.C.M × H.C.F = product of the numbers
(i) 26 and 91
Let us first find the factors of 26 and 91
26 = 2 × 13
91= 7 × 13
L.C.M of 26, and 91 = 2 × 7 × 13
L.C.M of 26, and 91 = 182
H.C.F of 26, and 91 = 182
We know that, L.C.M × H.C.F = First number × Second number
182 × 13 = 26 × 91 = 2366 = 2366
Hence verified
(ii) 510 and 92
Let us first find the factors of 510 and 92
510 = 2 × 3 × 5 × 17
92 = 2 × 2 × 23
L.C.M of 510 and 92 = 2 × 2 × 3 × 5 × 23 × 17
L.C.M of 510 and 92 = 23460
H.C.F of 510 and 92 = 2
We know that, L.C.M × H.C.F = First Number × Second Number
23460 × 2 = 510 × 92
46920 = 46920
Hence verified.
(iii) 336 and 54
Let us first find the factors of 336 and 54
336 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7
54 = 2 × 3 × 3 ×3
L.C.M of 336 and 54 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7
L.C.M of 336 and 54 = 3024
H.C.F of 336 and 54 = 6
We know that, L.C.M × H.C.F = First Number × Second Number
3024 × 6 = 336 × 54
18144 = 18144
Hence verified
Question: 2
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
(iv) 40, 36 and 126
(v) 84, 90 and 120
(vi) 24, 15 and 36
Solution:
To Find: LCM and HCF of following pairs of integers
(i) 15, 12 and 21
Let us first find the factors of 15, 12 and 21
12 = 2 × 2 × 3
15 = 3 × 5
21 = 3 × 7
L.C.M of 12, 15 and 21 = 2 × 2 × 3 × 5 × 7
L.C.M of 12, 15 and 21 = 420
H.C.F of 12, 15 and 21 = 3
(ii) 17, 23 and 29
Let us first find the factors of 17, 23 and 29
17 = 1 × 17
23 = 1 × 23
29 = 1 × 29
L.C.M of 17, 23 and 29 = 1 × 17 × 23 × 29
L.C.M of 17, 23 and 29 = 11339
H.C.F of 17, 23 and 29 = 1
(iii) 8, 9 and 25
Let us first find the factors of 8, 9 and 25
8 = 2 × 2 ×2
9 = 3 × 3
25 = 5 × 5
L.C.M of 8, 9 and 25 =23 × 32 × 52
L.C.M of 8, 9 and 25 = 1800
H.C.F of 8, 9 and 25 = 1
(iv) 40, 36 and 126
Let us first find the factors of 40, 36 and 126
40 = 23 × 5
36 = 23 × 32
126 = 2 × 3 × 3 × 7
L.C.M of 40, 36 and 126 = 23 × 32 × 5 × 7
L.C.M of 40, 36 and 126 = 2520
H.C.F of 40, 36 and 126 = 2
(v) 84, 90 and 120
Let us first find the factors of 84, 90 and 120
84 = 2 × 2 × 3 × 7
90 = 2 × 3 × 3 × 5
120 = 2 × 2 × 2 × 3 × 5
L.C.M of 84, 90 and 120 = 23 × 32 × 5 × 7
L.C.M of 84, 90 and 120 = 2520
H.C.F of 84, 90 and 120 = 6
(vi) 24, 15 and 36
Let us first find the factors of 24, 15 and 36
24 = 23 × 3
15 = 3 × 5
36 = 2 × 2 × 3 × 3
LCM of 24, 15 and 36 = 2 × 2 × 2 × 3 × 3 × 5
LCM of 24, 15 and 36 = 360
HCF of 24, 15 and 36 = 3
Question: 3
Given that HCF (306, 657) = 9, find LCM (306, 657 )
Solution:
Given:
HCF of two numbers 306 and 657 is 9
To find: LCM of number
We know that,
LCM × HCF = first number × second number
LCM × 9 = 306 × 657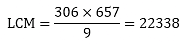
Question: 4
Can two numbers have 16 as their HCF and 380 as their as their LCM? Give reason.
Solution:
To find: can two numbers have 16 as their HCF and 380 as their LCM
On dividing 380 by 16 we get 23 as the quotient and 12 as the remainder
Since LCM is not exactly divisible by the HCF, two number cannot have 16 as their HCF and 380 as their
Question: 5
The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, find the other.
Solution:
Given:
LCM and HCF of two numbers 145 and 2175 respectively.
If one number is 725
To find: other number
We know that,
LCM × HCF = first number × second number
2175 × 145 = 725 × second number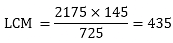
Question: 6
The HCF of two numbers is 16 and their LCM is 3072. Find the LCM.
Solution:
Given: HCF of two numbers is 16. If the product of the numbers is 3072
To find: LCM of number
We know that,
LCM × HCF = first number × second number
LCM × 16 = 3072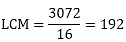
Question: 7
The LCM and HCF of two numbers are 180 and 6 respectively. If one of the numbers is 30, find the other number.
Solution:
Given:
LCM and HCF of two numbers 180 and 6 respectively.
If one number is 30
To find: other number
We know that,
LCM × HCF = First Number × Second Number
180 × 6 = 30 × Second Number

Question: 8
Find the smallest number which when increased by 17 is exactly divisible by both 520 and 468.
Solution:
To Find Smallest number which when increased by 17 is exactly divisible by both 520 and 468. L.C.M OF 520 and 468
520 = 23 × 5 × 13
468 = 2 × 2 × 3 × 3 × 13
LCM of 520 and 468 = 23 × 32 × 5 × 13 = 4680
Hence 4680 is the least number which exactly divides 520 and 468 i.e. we will get a remainder of 0 in this case. But we need the Smallest number which when increased by 17 is exactly divided by 520 and 468.
Therefore = 4680 – 17 = 46631
Hence 4663 is Smallest number which when increased by 17 is exactly divisible by both 520 and 468.
Question: 9
Find the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
Solution:
To Find: The smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
L.C.M of 28 and 32.
28 = 2 × 2 × 7
32 = 25
L.C.M of 28, and 32 = 25 × 7 = 224
Hence 224 is the least number which e×actly divides 28 and 32 i.e. we will get a remainder of 0 in this case. But we need the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
Therefore = 224 – 8 – 12 = 204
Hence 2041 is the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively
Question: 10
What is the smallest number that, when divided by 35, 56 and 91 leaves remainders of 7 in each case?
Solution:
To Find:
Smallest number that. When divided by 35, 56 and 91 leaves remainder of 7 in each case L.C.M OF 35, 56 and 91
35 = 5 × 7
56 = 23 × 7
91 = 13 × 7
L.C.M of 35, 56 and 91 = 23 × 7 × 5 × 13 = 3640
Hence 84 is the least number which exactly divides 28, 42 and 84 i.e. we will get a remainder of 0 in this case. But we need the smallest number that, when divided by 35, 56 and 91 leaves remainder of 7 in each case.
Therefore = 3640 + 7 = 3647
Hence 36471 is smallest number that, when divided by 35, 56 and 91 leaves remainder of 7 in each case.
Question: 11
A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. It is to be paved with square tiles of the same size. Find the least possible number of such tiles.
Solution:
Given: A rectangular yard is 18 m 72 cm long and 13 m 20 cm broad .It is to be paved with square tiles of the same size.
TO FIND: Least possible number of such tiles.
Length of the yard = 18 m 72 cm = 1800 cm + 72 cm = 1872 cm (therefore, 1 m = 100 cm)
Breadth of the yard = 13 in 20 cm = 1300 cm + 20 cm = 1320 cm
The size of the square tile of same size needed to the pave the rectangular yard is equals the HCF of the length and breadth of the rectangular yard.
Prime factorization of 1872 = 24 × 32 × 13
Prime factorization of 1320 = 23 × 3 × 5 × 11
HCF of 1872 and 1320 = 23 × 3 = 24
Therefore, Length of side of the square tile = 24 cm
Number of tiles required = Area of the courtyard, Area of each tile = Length × Breadth
Side2 = 1872 cm × 1320 cm 24 cm = 4290.
Thus, the least possible number of tiles required is 4290.
Question: 12
Find the greatest number of 6 digits exactly divisible by 24, 15 and 36.
Solution:
To Find:
Greatest number of 6 digits exactly divisible by 24, 15 and 36
The greatest 6 digit number be 999999 divisible by 24, 15 and 36
24 = 2 × 2 × 2 × 3
15 = 3 × 5
36 = 2 × 2 × 3 × 3
L.C.M of 24, 15 and 36 = 360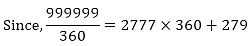
Therefore, the remainder is 279. Hence the desired number is = 999999 – 279 = 9997201
Hence 9997201 is the greatest number of 6 digits exactly divisible by 24, 15 and 36.
Question: 13
Determine the number nearest to 110000 but greater 100000 which is exactly divisible by each of 8, 15 and 21.
Solution:
To Find:
The number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
L.C.M of 8, 15 and 21.
8 = 2 × 2 × 2
15 = 3 × 5
21 = 3 × 7
L.C.M of 8, 15 and 21 =23 × 3 × 5 × 71= 840
When 110000 is divided by 840, the remainder is obtained as 800.
Now, 110000 — 800 = 109200 is divisible by each of 8, 15 and 21.
Also, 110000 + 40 = 110040 is divisible by each of 8, 15 and 21.
109200 and 110040 are greater than 100000.
Hence, 110040 is the number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
Question: 14
Find the least number that is divisible by all the numbers between 1 and 10 (both inclusive)
Solution:
To Find: Least number that is divisible by all the numbers between 1 and 10 (both inclusive) Let us first find the L.C.M of all the numbers between 1 and 10 (both inclusive)
1 = 1
2 = 2
3 = 3
4 = 2 × 2
5 = 5
6 = 2 × 3
7 = 7
8 = 2 × 2 × 2
9 = 3 × 3
10 = 2 × 5
L.C.M 2520
Hence 2520 is the least number that is divisible by all the numbers between 1 and 10 (both inclusive)
Question: 15
A circular field has a circumference of 360km. three cyclists start together and can cycle 48, 60 and 72 km a day, round the field. When will they meet again?
Solution:
Given: A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48, 60, and 72 km a day, round the field.
TO FIND: When they meet again.
In order to calculate the time when they meet, we first find out the time taken by each cyclist in covering the distance.
Number of days 1st cyclist took to cover 360 km = Total distance covered in 1 day = 360/48 = 7.5 = 7510 = 152 days
Similarly, number of days taken by 2nd cyclist to cover same distance = 360/60 = 6 days
Also, number of days taken by 3rd cyclist to cover this distance = 360/72 = 5 days
Now, LCM of 152, 6 and 5 = LCM of numerators
HCF of denominators = 30/1 = 30 days
Thus, all of them will take 30 days to meet again.
Question: 16
In a morning walk three persons step off together, their steps measure 80cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that he can cover the distance in complete steps?
Solution:
Given:
In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm and 90 cm.
To Find minimum distance each should walk so that all can cover the same distance in complete steps.
The distance covered by each of them is required to be same as well as minimum. The required distance each should walk would be the L.C.M of the measures of their steps i.e. 80 cm, 85 cm, and 90 cm,
So we have to find the L.C.M of 80 cm, 85 cm, and 90 cm.
80 = 24 × 5
85 = 17 × 5
90 = 2 × 3 × 3 × 5
L.C.M of 80, 85 and 90 = 24 × 3 × 3 × 5 × 17 = 12240 cm
Hence minimum 12240 cm distance each should walk so that all can cove the same distance in complete steps.
|
5 videos|292 docs|59 tests
|
FAQs on Exercise 1.3 & 1.4 - Real Numbers RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are the solutions to Exercise 1.3 in RD Sharma's Real Numbers Class 10 book? |  |
| 2. How can I find the solutions to Exercise 1.4 in RD Sharma's Real Numbers Class 10 book? |  |
| 3. Are the solutions to Exercise 1.3 and Exercise 1.4 available online? |  |
| 4. Where can I find RD Sharma solutions for Class 10 Real Numbers exercises? |  |
| 5. Can I download the solutions to Exercise 1.3 and Exercise 1.4 in RD Sharma's Real Numbers Class 10 book? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|

















